Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект лекций Электродинамика и РРВ

.pdf

Скачиваний:

355

Добавлен:

10.05.2015

Размер:

3.16 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 219 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Emx =	−iГ2	∂Emz		ωµ0µ	∂Hmz		(15б)
			+			.

	χ	∂x		Г ∂y

Второе уравнение (13) и первое (14) образуют систему линейных уравнений относительно поперечных компонент Emy и Hmx. Ее решение

Emy = −χiГ2

Hmx = −χiГ2

∂Emz +			ωµ0µ		∂Hmz			,

						∂x
	∂y			Г
	∂Hmz			ωε0ε		∂Emz
		+					.

	∂x			Г		∂y

Формулы (15) и (16) удобно свернуть к следующей форме записи

Emt =	−iГ		Emz − iωµ0µ ( × H mz )					,
		χ2		χ2
H mt =		iωε0ε		( × Emz )	−	iГ	H mz .
		χ2				χ2

(16а)

(16б)

(17)

Выражения (17) уже не связаны с определенным выбором поперечных координат: вместо x и y можно взять произвольные криволинейные ортогональные координаты в плоскости z = const.

Волна, переносящая энергию в направлении z, обязательна должна иметь как поперечную электрическую, так и поперечную магнитную компоненты: в противном случае Пz = 0 Выражения (15) и (16) показывают, что таким свойством может обладать электромагнитное поле с одной только электрической или только магнитной продольной компонентой. При этом общее решение может рассматриваться как наложение двух частных, для одного из которых Ez ≠ 0 и Hz = 0 , а для другого Hz ≠ 0 и Ez = 0 .

Поэтому, рассматривая различные волны в продольно–однородных структурах, выделяют класс так называемых Е – волн, или электрических волн, для которых Ez ≠ 0 и Hz = 0 , и класс Н – волн, или магнитных волн, для кото-

рых Hz ≠ 0 и Ez = 0 . Вместо символов Е и Н употребляются также ТМ и, соот-

ветственно, ТЕ (говорят поперечно–магнитные и поперечно–электрические

волны).

Более сложные волновые процессы, имеющие как электрическую, так и магнитную продольные компоненты, принято называть гибридными волнами.

Лекция № 16. Электромагнитные волны в продольно–однородных структурах (продолжение)

Если волна в продольно–однородной структуре совершенно лишена продольных компонент (Ez = 0; Hz = 0), то ее называют поперечно– электромагнитной, Т– или ТЕМ–волной.

В этом случае χ = 0 и

Г = k ,

(1)

т.е. любые Т–волны в некоторой среде распространяются с той же фазовой скоростью, что и плоская однородная волна. Т–волны обладают двумя важными свойствами. Во-первых, они могут существовать только в однородных средах, т.к. равенство (1) не может быть выполнено, если k (вместе с ε и µ) принимает разные значения в разных подобластях продольно–однородной структуры. Вовторых, поперечное распределение полей в случае Т–волн должно повторять продольно–однородные (не зависящие от z) статические распределения, т.к. они описываются двумерными уравнениями Лапласа

2 E = 0 , 2 H = 0 ,

(2)

которые получаются из соответствующих из уравнений Гельмгольца при ω = 0 и отсутствии продольной зависимости.

Отсюда можно сделать вывод, что Т–волны могут распространяться в тех продольно–однородных структурах, в которых возможно существование отличного от нуля электростатического поля.

От Т–волн все остальные волновые процессы формально отличаются невыполнением равенства (1). Поэтому

Г = k2 − χ2 .

(3)

Если рассматривать только незатухающие волны, для которых постоянная распространения Г – величина вещественная, то ясно, что при χ2 > 0 они

будут быстрыми:	Г < k и vф > v (vф- фазовая скорость данной волны,						v - ско-
рость Т–волны в данной среде). При					χ2 < 0, т.е. при мнимых поперечных вол-
новых числах χ волны будут медленными: Г > k и vф < v.
Комплексные амплитуды волн различных классов имеющие вид
E m = E (x, y )e − iГz ,						H m = H (x, y )e − iГz ,	(4)
нетрудно выразить	при помощи полученных на предыдущей лекции соотно-
шений через продольные компоненты.
Рассматривая Е–волны, положим Hmz = 0 и, выписывая Em , добавим к
Emt величину Emz .	В результате получаем
	−i(Г χ	2		−iГz		,
Em = z0E z	−i(Г χ		) E z e			,	(5)
Hm = (iωε0ε χ2 ) ( ×E z ) e−iГz = −(iωε0ε χ2 ) (z0 × E z )e−iГz .							(5)

Отсюда видно, что

				Emt = Z E (H mt × z0 ) ; Z E = Г ωε0ε ,	(6)
т.е. поперечные компоненты векторов Е и Н ортогональны, причем					скалярные
величины	E	и H	mt	различаются только постоянным множителем ZE. Следо-
	mt		mt

вательно, распределение интенсивности электрического и магнитного поперечных полей в сечении z = const описывается одной и той же функцией. Величина

ZE называется волновым сопротивлением в классе Е–волн.

Ввиду (5) достаточно знать функцию E z и поперечное волновое число χ,

чтобы определить все поле.	Пусть все проводники	являются идеальными
(δ →∞), внутренняя среда –	по постановке задачи –	однородна. Проецируя
уравнение

2 E +χ2E = 0

на ось z, и учитывая условие на границе с проводником, записываем:

2 E	+χ2E	z	= 0,	E	z	= 0 на L .	(7)
z		z			z

Это не что иное, как формулировка первой краевой задачи для скалярного уравнения Гельмгольца; под L понимается идеально проводящий контур поперечного сечения полого волновода или совокупность контуров в более сложных случаях. Из интегрального соотношения


	∫	E z			2 d S
					2 d S

χ 2 =	S
χ 2 =	∫		E z	2 d S
				2 d S

следует, что χ2 ≥ 0 . При этом χ2 = 0 соответствует предельному случаю Т–волн (E z → 0). Для Е–волн χ2 > 0, т.е. это волны быстрые.

Итак, для определения Е–волн той или иной направляющей структуры с однородной средой и при идеализации проводящих границ надо найти решение первой краевой задачи для скалярного уравнения Гельмгольца (7). При этом

определяются собственные функции E z(n) и отвечающие им собственные значения χ2n (n =1,2,...) . Затем применяются формулы (5).

Переходя к Н-волнам, положим Emz = 0 и запишем комплексные амплитуды полных полей, добавляя Hmz к Hmt :

	Em = −(iωµ0µ χ2 )( ×H z ) e−iГz = −(iωµ0µ χ2 )( H z × z0 )e−iГz ,	(8)
	Hm = z0H z − i(Г χ2 ) H z e−iГz .	(8)
	Hm = z0H z − i(Г χ2 ) H z e−iГz .
	откуда
	Emt = Z H (Hmt × z0 ), Z H = ωµ0µ Г.	(9)

Здесь ZH - волновое сопротивление в классе Н–волн. Как и в случае Е– волн делаем вывод об ортогональности векторов Et и Ht , а также об идентичности распределений их скалярных амплитуд в любой поперечной плоскости.

Поскольку все поле определяется через H z , сформулируем задачу, приводящую к нахождению этой продольной компоненты. Проецируя уравнение

2 H + χ2H = 0

на ось z, получим скалярное уравнение Гельмгольца

2 H z + χ2H z = 0.

Для определения граничного условия, налагаемого на H z на идеально

проводящей границе, положим x = τ и у = ν, где τ и ν - локальные декартовы координаты в некоторой точке контура L , тангенциальная и нормальная (нормаль - внутренняя). Рассмотрим первое уравнение Максвелла

	∂H mz	+ iГH mν = iωε0εEmτ.	(10)
	∂ν

Так как на поверхности идеального проводника			Еτ = 0, Нν = 0, то из (10)

следует, что ∂Hmz ∂ν = 0. Поэтому для функции H z получаем вторую краевую задачу. Как и волны Е, Н–волны являются быстрыми. Полное поле для совокупности собственных функций H z(n) с собственными значениями χ2n (n =1,2,...) находится по формуле (9).

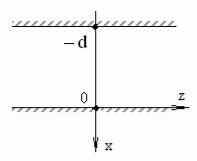
Для иллюстрации изложенного материала обратимся к плоским структурам, уже рассматривавшимся ранее.

Рис. 1. Система двух идеально проводящих плоскостей

Для системы двух идеально проводящих плоскостей (рис. 1) краевая задача для Е–волн принимает вид

d 2E	z	+ χ	2	E	z	= 0,	(11)
dx 2

E z (0) = E z (−d ) = 0 .

Ее решение:

E (n) = B

sin χ

χ2

nπ 2

(n =1, 2,…)

(12)

дает собственные функции и собственные значения, отвечающие Е–волнам. Краевая задача для Н–волн

	d 2H z + χ2H		z	= 0,			(13)
	dx2		z				(13)
	H z′(0) =H z′(−d) = 0
дает собственные функции и собственные значения
(n)	= Ancosχn x,	2		nπ	2	(n =1, 2,…).	(14)
H z	= Ancosχn x,	χn		=	,	(n =1, 2,…).	(14)
				d

Способ получения решений (12) и (14) очень прост: берется общее решение уравнения в форме Аcos(χx) + Bsin(χx) и производится наложение граничных условий, что сразу приводит к отбрасыванию одного члена и конкрети-

зации χ. Чтобы получить полные поля, достаточно внести						E z(n) в (5), и H z(n) в
(8).
Случай, соответствующий		n = 0	(параллельная поляризация) относится
к классу Т–волн. Краевая задача – одномерный аналог задачи Дирихле
d 2ϕ	= 0,	ϕ(0)	= C ,	ϕ(−d) = C	,	(15)

dx2			1	2

где C1 и С2 - произвольные, но различающиеся константы. Общее решение дифференциального уравнения есть ϕ = Ах + В, а с учетом граничных условий:

Тогда	ϕ = (C1 −C2 )x d +C1.	(16)
Тогда
E = x0E = − ϕ= x0 (C2 −C1 ) d ,
	= 1 (z0 ×E ), где Z =120π	(17)
H	= 1 (z0 ×E ), где Z =120π	µ .
	Z	ε
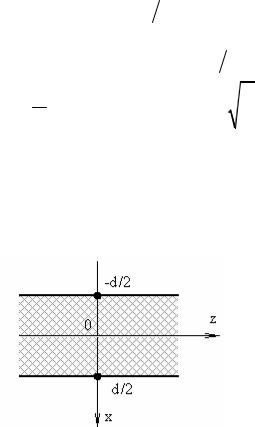
Перейдем к случаю	плоского диэлектрического волновода (рис. 2.). Это

структура с двумя разнородными областями, в каждой из которых ищутся решения уравнений Гельмгольца для E z и H z . Рассматривая Е–волны мы долж-

ны сформулировать уравнение Гельмгольца относительно E z дважды.

Рис. 2. Плоский диэлектрический волновод

Для внутренней области (-d/2 < x < d/2) запишем два типа решений (четные и нечетные):

E z = Acosχ1x, Bsin χ1x.

(19)

Вне слоя (достаточно рассмотреть область x < d/2) решения сформулируем в виде

Ez =Ce−iχ2x =Ce	χ2	x ,	(20)

т.е. χ2 = i|χ|: поле должно быть убывающим. Для полупространства x > d/2 решение четным или нечетным образом повторяет функцию (20) – в зависимости от выбора решения (19).

Для согласования констант в (19) и (20) надо наложить условия непрерывности тангенциальных компонент Eτ = Ex и Нτ = Ну на границе раздела сред x = d/2. Сначала выразим Hmy :

H = − iωε0ε

(z 0 × E z )e−iГz ;

χ2

H y = − iωε0ε

∂E z

χ2

∂x

При -d/2 < x < d/2

H y = A iωε0ε1 sin χ1 x ,

− B iωε0ε1 cos χ1 x,

(21)

при x < d/2

χ1

= −C (iωε0 ε2

χ2 )e −i χ2 x .

H y

(22)

Наложение указанных граничных условий дает

в двух вариантах четно-

сти:

= C e

i(χ

d 2 )

A cos

(23)

ε1

χ1d = C

ε2

ei(χ2 d

2 ).

sin

C e

i(χ

d 2 )

− B sin

(24)

ε1

cos χ1d

ε2

e i(χ2 d

2 ).

= C

Избавляясь от неопределенных коэффициентов, получаем трансцен-

дентные уравнения относительно поперечных волновых чисел

tg χ1d

= −i

χ1

ε2

ctg

χ1d

= i

χ1

ε2 .

(25)

Поскольку χ2

= k2

− Г2 ,

то

χ2

−χ2 = k2

− k

и, следовательно,

в (25)

1,2

можно оставить только χ1 или χ2 = i|χ2|.

Уравнения (25) позволяют при заданных проницаемостях обеих сред и толщине слоя найти поперечные волновые числа, а следовательно, и постоянные распространения Г волн, направляемых слоем. Полные поля находятся с привлечением формул (5).

Все выполненные операции нетрудно повторить для случая Н–волн. В этом, однако, нет необходимости, так как вместо этого достаточно применить принцип двойственности. В частности трансцендентные уравнения (25) примут вид

χ1d

= −i

χ1

µ2

ctg

χ1d

= i

χ1

µ2 .

(26)

Лекция № 17. Передача и потери энергии в структурах

Потери энергии через поперечное сечение продольной структуры выражает передаваемую мощность. Имеет смысл рассматривать средний поток энергии. Таким образом

		∫		2	∫	2	∫
P	=		П	z dS = 1 Re		(Em ×H*m )z dS = 1 Re		(Emt × H*mt )z dS ,	(1)
		S			S		S

где S – поперечное сечение структуры, которое может быть и бесконечным. Если среда однородна и в структуре распространяется одна Т-, Е- или Н-волна, то из (1) следует

R e Z

∫

H m2 t dS =

R e

∫

E m2 t dS ,

(2)

Z *

где Z - волновое сопротивление Z, ZE или ZH. Таким образом, передача энергии в продольно-однородной структуре осуществляется лишь теми волнами, для

~ =

которых ReZ 0.

Потери энергии в структурах можно вычислить путем применения общего выражения для мощности потерь

Pп = ω2 V∫(ε0ε′′EmE*m +µ0µ′′HmH*m )dv.

Для продольно-однородных структур можно определить потери pп :

′′

= lim

∫ (

+µ

m )

dS .

(3)

ε E

µ H

∆z→0

∆z

∆v

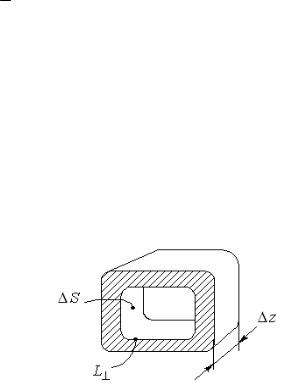
Здесь имеется в виду объем ∆V, заключенный между двумя поперечными сечениями z и z + ∆z. Как правило, объем ∆V содержит разнородные среды, например, в случае полого волновода (рис.1) – металл и внутренний диэлектрик.

Рис.1. Поперечное сечение полого волновода

На практике по формуле (3) чаще всего находятся только потери в диэлектрике. Что касается металла, то при сильном поверхностном эффекте простую формулу потерь можно получить, учитывая поток энергии, уходящий

внутрь металлических предметов:

= lim

∫

dS = lim

∫

×H*

)

dS =

mτ

∆z→0

∆z

∆z→0

∆z

mτ

∆S

(4)

1+i

∫

= 2 Re σ∆0

∫Hmdl

2 Rпр

Hmdl ,

где L - контур или совокупность контуров поперечного сечения всех металлических элементов, ν - направление внутренней по отношению к металлу нормали.

В результате потерь энергии происходит затухание волн, с которым мы уже знакомы на примере однородной Т-волны. В продольно-однородной структуре амплитуды векторов Е и Н уменьшается по закону exp(-Г”z), а передаваемая мощность - ввиду (2) – по закону exp(-2Г”z):

					′′	(5)
					′′
	P ( z) = P (0)e−2 Г z .
На отрезке пути ∆z в результате убывания Р(z) наблюдается отрицатель-
ное приращение передаваемой мощности:

		dP		′′		(6)
		dP		′′
∆P = dz			∆z +... = −2Г Р∆z +...

(отброшены члены высшего порядка). Приращение потерь на этом отрезке выразим через погонные потери Pп :

∆		= dPп			∆z +... = p ∆z +...			(7)
∆	Р	= dPп			∆z +... = p ∆z +...			(7)
	п		dz				п
			dz
в силу закона сохранения энергии
			∆		+ ∆			(8)
			∆	P	+ ∆	Pп = 0 .		(8)

При ∆z →0 выражения (6) и (7) становятся точными. Их подстановка в

(8) приводит к следующему, как говорят, «энергетическому» выражению коэффициента затухания:

Г′′ = рп / 2		.	(9)
	P

Соотношение является вполне строгим.

Погонные потери можно разделить на две части. Бывает удобно, напри-

мер, разделить потери в металле и диэлектрике, т.е.							pп = pпм + pпд . Вообще, ес-
ли pп = pп1	+ pп2 + … , то согласно (9)
			Г′′ =	1	∑рпn = ∑Гn′′,		(10)

				2Р
	Г′′ = рпn / 2				n	n
где члены			выражает парциальные коэффициенты затухания. В
		P
большинстве случаев
				Г′′ = Гм′′ + Гд′′,			(11)

где Гм′′ = рnм / 2			и	Гд′′ = рnд / 2		. Используя формулы (3) и (4) при µ”= 0, полу-
	Р				Р
чаем:
			ωε0 ∫ε′′Em E*mdS				;	Гм′′ =	Rпр ∫Hm H*mdS	.	(12)
Гд′′ =				S					L

		2Re ∫(Em ×H*m )z dS							2Re ∫(Em ×H*m )z dS
				S					S
В большинстве практических случаев точные значения Ет,Нт получить
гораздо труднее, чем решить идеализированную задачу, в которой											потери ис-

ключены. Но если такая задача решена, то соответствующие значения Ет,Нт

можно внести в (12) в качестве приближенных комплексных амплитуд. Это дает приближенные значения Гд′′, Гм′′. Таким образом, энергетический анализ дает

возможность приближенно оценивать затухание волн в различных структурах без потерь.

Пример. Вычислим коэффициент Гд′′ для некоторой Н-волны, распространяющейся в структуре с однородной средой. Поскольку в этом случае

Еmt = Еm , то

ωε0ε′′

= Re

∫Em2 dS ,

pпд =

∫Em2 dS .

)

При подстановке этих выражений в формулу Гд′′ = рnд / 2 Р

интегралы

сократятся. В результате получится

Гд′′

ω2ε0µ0µε′′

k 2

tg ∆

(13)

2Re Г*

2Re Г

где учтено, что Z

ωµ0µ

ε′µ′ .

а k = с

Если структура без потерь изучена и в области f > fкр известна постоян-

ная распространения =

k 2 −χ2 , то (13) можно заменить ReГ на что дает

следующую приближенную формулу:
Гд′′ = k 2 tg∆/ 2 .	(14)
Можно убедиться, что этот результат верен также и в случае Е-волн. В
случае Т–волн сделаем замену → k . Тогда (14) переходит в
Гд′′ = 1 k 2tg∆.	(15)
2

Если в результате решения задачи для некоторой продольно-однородной структуры найдено поперечное волновое число χ, то по формуле

Г = k2 −χ2

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 219 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.09.20193.31 Mб89Конспект лекций по инженерной геодезии.doc
#
30.07.20192.69 Mб48Конспект лекций по предмету Теоретическая механ....rtf
#
27.09.2019843.78 Кб79Конспект лекций ТП (4 семестр).doc
#
09.09.20191.43 Mб14Конспект лекций целиком_.doc
#
15.08.20191.08 Mб27Конспект лекций Э.П.Басалаев.doc
#
10.05.20153.16 Mб355Конспект лекций Электродинамика и РРВ.pdf
#
20.11.2019507.39 Кб43Конспект лекций ЭП (по желанию).doc
#
10.11.20184.16 Mб41Конспект лекций.doc
#
14.11.2019988.67 Кб104КОНСПЕКТ ЛЕКЦИЙ.doc
#
10.05.2015454.14 Кб15Конспект Лекций_ по Педагогике..doc
#
23.12.2018108.03 Кб8конспект нотариат.doc