
Конспект лекций Электродинамика и РРВ
.pdf
При вычислении добротности резонаторов различные факторы, определяющие потери, можно учитывать отдельно. Пусть Pп = Pп1 + Pп2 + PпΣ , где име-
ются в виду потери в диэлектрических элементах, в металлических элементах и на излучение, соответственно. Введем парциальные добротности
Q = |
ωW |
, |
Q = |
ωW |
, |
Q = |
ωW |
, |
(15) |
д |
Pд |
|
м |
Pм |
|
Σ |
PΣ |
|
|
|
п |
|
|
п |
|
|
п |
|
|
каждая из которых вычисляется с учетом одного из факторов. Тогда для полной добротности имеем
1 |
= |
1 |
+ |
1 |
+ |
1 |
, |
(16) |
Q |
|
Qм |
|
|||||
|
Qд |
|
QΣ |
|
||||
т.е. обратные добротности складываются. Правда этот вывод нельзя считать строгим: действие разных факторов приводит к некоторому перераспределению поля, а следовательно, величина W не будет одной и той же при вычислении разных парциальных добротностей и полной добротности. На практике запас энергии W обычно вычисляют, исходя из распределения поля в резонаторе без потерь. В этом приближении и применяются формулы (15) и (16).
Считая отсутствующими магнитные потери, для парциальной добротности Qд можем записать
|
ωW |
|
ω |
ε0 ε′ |
V∫ |
E m E m dV |
ε′ |
|
|
||
Qд = |
= |
|
2 |
′′ |
= |
= 1 tg ∆ . |
(17) |
||||
Pпд |
ωε0 ε |
∫ |
ε′′ |
||||||||
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
E m E m dV |
|
|
|
||
|
|
|
|
|
V |
|
|
|
|
||
Замена величины Рп средней мощностью Pп закономерна в обычных условиях, когда ω”<< ω’ (Q >> 1).
Для определения парциальной добротности Qм будем вычислять запас энергии W через магнитную энергию, как Wmaxм = 2W м , а потери – из теории сильного скин–эффекта
|
ω |
µ0µ |
V∫ |
H m H m dV |
|
µ 1 |
|
V∫ |
H m H m dV |
|
|||
Qм = |
|
2 |
|
= 2 |
|
|
, |
(18) |
|||||
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
µм ∆0 |
|
∫ |
|
||||||
|
Rпр ∫ |
|
|
|
H m H m dS |
|
|||||||
|
2 |
H m H m dS |
|
|
|
|
|
|
|
|
|||
|
|
S |
|
|
|
|
|
|
S |
|
|
|
|
где µм - относительная магнитная проницаемость металла. Обычно µм = µ = 1. Отношение интегралов в (18) при сохранении формы резонатора и типа
колебаний пропорционально линейному размеру и, следовательно, обратно пропорционально собственной частоте ω. Учитывая частотную зависимость ∆о, видим, что добротность Qм изменяется, как ∆ ω .
ω .
Вычисление парциальной добротности QΣ не сводится к применению некоторой общей формулы. Резонатор нужно рассматривать одновременно со связанной через отверстие электродинамической структурой.

Лекция № 21. Открытые резонаторы
Для освоения волн субмиллиметрового и светового диапазонов созданы приборы квантовой электроники, основной частью которых являются открытые резонаторы, составленные из систем зеркал.
1. Поле в резонаторе, образованном прямоугольными зеркалами.
Рассмотрим открытый резонатор, образованный двумя прямоугольными зеркалами с размерами 2а и 2b, отстоящими друг от друга на расстоянии 2l
(рис.1).
Рис. 1. Прямоугольные пластины, образующие открытый резонатор
Начало координат системы х, у, z расположим в центре резонатора. Как обычно, задача состоит в нахождении картины распределения электромагнитного поля внутри резонатора. Естественно, что внутри резонатора любая из функций поля Ф (х, у, z) (например, Ex, Ey и др.) будет удовлетворять волновому уравнению вида
2Φ(x, y, z)+ k 2Φ(x, y, z)= 0 |
(1) |
Решение (4.61) следует искать в форме, предусматривающей гармоническую функциональную зависимость поля от z
Φ(x, y, z)=W (x, y, z)exp(jkz)− (−1)qW (x, y,−z)exp(− jkz). |
(2) |
Кроме гармонической зависимости от z, определяемой множителями exp(± jkz), предполагается также слабо затухающая от зеркал к центру резона-
тора зависимость, определяемая изменением от z амплитудной функции W (x, y,±z). Возможная симметричность и антисимметричность поля относи-
тельно начала координат учтена в (2) множителем (-1)q.
Одновременно в решении (2) учитывают, что на поверхности зеркал функция поля Φ(x, y,±l) должна обращаться в нуль. Это условие можно выпол-
нить, если функции W (x, y,±l) удовлетворяют соотношению
W (x, y,−l)= exp(j(2kl − qπ ))W (x, y,l). |
(3) |
В самом деле, подставляя (3) в (2), получим

Φ(x, y,±l)=W (x, y,l) exp( jkl)−(−1)q exp( j(2kl − qπ))exp(− jkl ) = =W (x, y,l)exp( jkl) 1−(−1)q exp(− jqπ) ,
откуда при q = 0, 1, 2, … |
|
Φ(x, y,±l) =W (x, y,l)exp( jkl)[1−1]= 0. |
(4) |
Заметим также, что множитель 2kl − qπ для обеспечения целого числа
полуволн между зеркалами резонатора должен быть кратен или просто равен π . Для этого следует положить
2kl − qπ =π . |
(5) |
Тогда фазовый набег, обеспечивающий резонансные условия в открытом резонаторе,
kl = 2π |
l |
=π |
q +1 |
>>1, |
(6) |
λ |
|
||||
|
2 |
|
|
||
откуда следует, что индекс q >>1, так как l λ >>1.
λ >>1.
Вычислим производные решения (2), входящие в уравнение (1). Для сокращения записи обозначим W (х, у, z) = W и будем дифференцировать и подставлять лишь первое слагаемое решения (2)
∂∂Φz = ∂∂Wz exp(jkz)+ jkW exp(jkz),
∂2Φ |
= |
∂2W |
exp(jkz)+ jkW exp(jkz)− k 2W exp(jkz), |
(7) |
||
∂z2 |
∂z2 |
|||||
|
|
|
∂2Φ |
= |
∂2W exp( jkz), |
|
|
|
|
∂x2 |
|
∂x2 |
|
∂2Φ = ∂2W exp(jkz), ∂y2 ∂y2
Подстановка решения (2) и производных (7) в (1) приводит к уравнению относительно W (х, у, z)
∂2W (x, y, z) |
+ |
∂2W (x, y, z) |
+ |
∂2W (x, y, z) |
+ 2 jk |
∂W (x, y, z) |
= 0 . |
(8) |
∂z2 |
|
∂x2 |
|
∂y2 |
|
∂z |
|
|
Уравнение эллиптического типа (8) можно упростить и привести к параболическому типу, если предположить, что зависимость W(х, у, z) от z слабая. Действительно, не следует ожидать сильного затухания поля в пространстве между зеркалами, и поэтому
∂2W (x, y, z) |
≈ 0 . |
(9) |
∂z2 |
|
|
Тогда получим
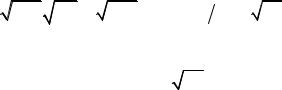
∂2W (x, y, z) |
+ |
∂2W (x, y, z) |
+ 2 jk |
∂W (x, y, z) |
= 0 . |
(10) |
∂x2 |
|
∂y2 |
|
∂z |
|
|
В дальнейшем для упрощения рассуждении не будем рассматривать векторную ориентацию компонент поля в резонаторе, а рассмотрим лишь распределение интенсивности амплитуды поля внутри него. Для решения (10) используем подстановку Фурье
W (x, y, z)=W (x, z)W (y, z). |
(11) |
Использование (11) разбивает (10) на два уравнения с постоянной разделения равной нулю
∂2W (x, z) |
+ 2 jk |
∂W (x, z) |
= 0 , |
(12) |
∂x2 |
|
∂z |
|
|
∂2W (x, z) |
+ 2 jk |
∂W (y, z) |
= 0 . |
(13) |
∂y2 |
|
∂z |
|
|
Будем искать решение (12), (13) в форме, которая обеспечивает принятое ранее предположение о слабом затухании (с коэффициентом затухания δ)
W (x, y, z) от z
W (x, z)= Aexp(αx ±δz), |
(14) |
где δz 1.
Здесь следует принять знак «плюс» для z > 0 и «минус» для z < 0 с тем, чтобы решение (14) определяло затухание поля от зеркал к середине резонатора.
Проведем вычисление функции W (х, z). Найдем производные
|
|
∂W (x, z) |
|
= ±δAexp(αx ±δz), |
|
|
||
|
|
∂z |
|
|
||||
|
|
|
|
|
|
|
||
|
∂2W (x, z) |
|
= α2 Aexp(αx ± δz) |
|
(15) |
|||
|
|
∂x2 |
|
|||||
|
|
|
|
|
|
|
||
и подставим их в (12). В результате |
|
|
|
|||||
|
|
±δ = − |
1 |
α2 |
, |
|
(16) |
|
|
|
|
|
|||||
откуда |
2 jk |
|
|
|
||||
|
|
|
|
|
||||
|
|
α2 = 2 jkδ, |
|
|
(17) |
|||
и коэффициент изменения амплитуды поля W (х, z) вдоль х |
|
|||||||
α = 2kδ j = 2kδexp( j π 4)= kδ(1 j). |
(18) |
|||||||
Подставляя (18) в (14), получаем |
|
|
|
|||||
W (x, z) = Aexp |
kδ(1 j)x ±δz |
. |
(19) |
|||||
|
|
|
|
|
|
|
|
|
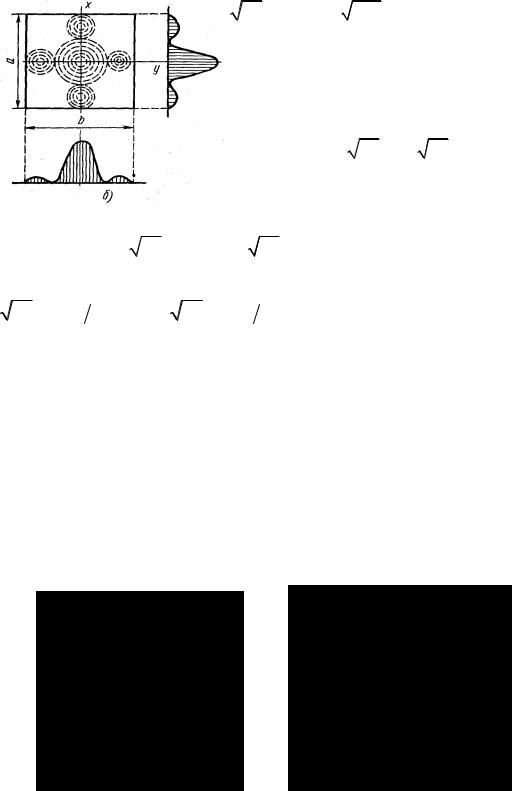
Знаки j в гармонической части формулы (19) определят две возможные волны, распространяющиеся вдоль х в двух направлениях. Если принять равными амплитуды этих волн, что следует предположить существование вдоль х стоячей волны, как результата их суперпозиции. В этом предположении перепишем
(19).
W (x, z)= 2Aexp(± kδx ±δz)cos kδx . |
(20) |
Амплитуда этой волны соответственно знакам перед корнем в показателе степени уменьшается в обе стороны от середины х = 0. Проводя аналогичные выкладки для решения уравнения (13), на основе (11) найдем полное решение
(10)
W (x, y, z) =W (0)exp(± kδ(x + y)± 2δz cos kδxcos kδy). |
(21) |
|
Теперь следует учесть, что за границами пластин резонатора npи x ≥ a и |
||
y ≥b поле должно стремиться к нулю. Из этого вытекают требования |
|
|
cos kδa = 0 , cos kδb = 0 , |
(22) |
|
что выполняется при |
|
|
kδa = π(1 2 + n), |
kδb = π(1 2 + m), n,m = 0,1,2,3,... |
(23) |
Из совместности этих выражений вытекает условие |
|
|
a |
= 1+ 2n , |
(24) |
b |
1+ 2m |
|
определяющее соотношение номеров вида колебаний m и n с размерами сторон.
Выражение (21) с учетом (23) позволяет построить распределение интенсивности амплитуды колебаний по трем координатам резонатора для различных видов колебаний. Для примера на рис. 2, а и б построено paспределение интенсивности поля на прямоугольных зеркалах для видов колебаний с индексами 01q и 11q.
Рис. 2. Распределение интенсивности поля ,в открытом резонаторе с прямоугольными пластинами: а — вид колебаний 01q; б— вид колебаний 11q
В ряде случаев зеркала открытых резонаторов берут круглой формы, причем сами зеркала часто делают сферическими, что позволяет осуществить лучшую концентрацию поля в пространстве между зеркалами.

Лекция № 22. Эквивалентная схема нерегулярности в волноводе
Рассмотрим здесь в общем виде взаимосвязь между обусловленным нерегулярностью множеством полей различных типов и ее эквивалентной схемой. Пусть область нерегулярности V ограничена поперечными сечениями S' и S'' двух в общем случае различных волноводов 1 и 2, в каждом из которых распространяется бегущая волна только одного рабочего типа (рис. 1).
Рис. 1
В волноводе 1, кроме падающей волны рабочего типа, существуют обусловленные нерегулярностью отраженная волна рабочего типа и местные поля высших типов. В согласованном с нагрузкой волноводе 2 существуют падающая волна рабочего типа (прошедшая сквозь нерегулярность) и местные поля высших типов. Полное поле при этом можно представить в виде разложения по собственным волнам волноводов:
′ ′ |
∞ |
′ |
− |
′ ′ |
∞ |
′ |
′ |
, |
E = E 1+ |
+ ∑E v |
=U1e1 + |
∑Uv |
−ev |
||||
|
v=1 |
|
|
|
v=2 |
|
|
(1) |
|
∞ |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
||
H′ = H′1+ + ∑H′ v− = I1′h1′ + ∑Iv′−h′v , |
||||||||
где |
v=1 |
|
|
|
v=2 |
|
|
|
|
|
|
|
|
|
|
|
|
U1′ =U1′+ +U1′−, |
|
I1′ = I1′+ + I1′−, |
|
|
|
|||
∞ |
|
|
|
∞ |
|
|
|
|
E′′ = ∑E′′v+ =U1′′+e1′′+ ∑Uv′′+e′′v , |
|
|
|
|||||
v=1 |
|
|
|
v=2 |
|
|
|
(2) |
∞ |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
||
H′′ = ∑H′′v+ = I1′′+h1′′+ + ∑Iv′′+h′′v . |
|
|
||||||
v=1 |
|
|
|
v=2 |
|
|
|
|
Здесь и далее одним штрихом обозначены величины, относящиеся к сечению S' первого волновода, двумя штрихами — к сечению S″ второго волновода; волны рабочего типа обозначены индексом v = 1.
Связь токов и напряжений в эквивалентных длинных линиях представим в виде соотношения
Iv± (z) = ±YcvUv± (z), |
(3) |
где использована характеристическая проводимость Ycv = l/Zcv. Для бегущих волн рабочего типа характеристическая проводимость является вещественной:
Yc1 = g1; |
(4) |

для местных полей высших типов (v ≥ 2) характеристические проводимости оказываются мнимыми:
|
Ycv = ibv , |
v = 2, 3, ..., |
(5) |
|
причем |
для полей класса Н |
они |
имеют индуктивный |
характер |
(bh = −αh |
ωµa < 0), для полей класса Е — емкостный (be = ωεa αe > 0 ). |
|
||
Рассмотрим случай нерегулярности, |
при котором в боковых |
стенках |
||
волноводов нет щелей или отверстий. Применим теорему Умова—Пойнтинга к объему V, ограниченному идеально проводящими боковыми стенками и сече-
ниями S' и S'' , приняв во внимание, что внутри объема δст = 0 :
Pп.ср +i2ω(Wм.ср −Wэ.ср) + |
1 |
|
|
|
′ |
1 |
|
|
[E ''H |
′′ |
(6) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
∫′ |
|
|
|
|
|
|
2 |
∫′′ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
S |
|
|
|||||
Поскольку эквивалентная входная проводимость в сечении S' для волны |
|||||||||||||||||||||||||||||||
рабочего типа определяется выражением Y = I1′ |
U1′, |
|
|
||||||||||||||||||||||||||||
Y = I1′ U1′ = gн + gп +i(b'+ b"+bW ) = g +ib, |
|
(7) |
|||||||||||||||||||||||||||||
где |
|
|
|
U1′′+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2P |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
п.ср |
|
|
|
|
|
|
|
|
||||
gн = |
|
U1′ |
|
|
|
|
|
gп = |
|
U1′ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 g1, |
|
2 |
, |
|
|
|
|
|
|
||||||||||||||||||||
b |
' = ∑ |
Uv′− |
2 |
|
bv′, |
b" = ∑ |
Uv′′+ |
2 b"v , |
|
|
|||||||||||||||||||||
|
|
|
∞ |
|
|
|
|
|
2 |
|
|
|
|
|
∞ |
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v=2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
v=2 |
U1′ |
|
|
|
|
|
|
|
|
|
U1′ |
|
|
|
|
|
|||||||||||||
b |
|
= |
4ω(W |
э.ср |
−Wм.ср ) |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
W |
|
|
|
|
|
|
|
|
|
|
|
|
U1′ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из (7) следует, что активная часть эквивалентной проводимости обусловлена существованием в сечении S" второго волновода бегущей волны рабочего типа (gн) и потерями в объеме V (gп). Реактивная часть эквивалентной проводимости обусловлена существованием местных полей высших типов в сечениях S' первого волновода (b') и S" второго волновода (b") и разностью средних значений электрической и магнитной энергий в объеме V (bw).
Отобразив относительно сечения S' нерегулярность схемой замещения согласно (7) и представив расположенный перед речением S' волновод 1 с бегущими волнами рабочего типа эквивалентной длинной линией с волновой проводимостью Y'в = Y'с1 = g'1, получим эквивалентную схему рис. 2.
Рис. 2

Наиболее просто решаются электродинамические задачи о плоских нерегулярностях, имеющих нулевую протяженность вдоль оси волновода (например, бесконечно тонкие диафрагмы, скачкообразные изменения поперечного сечения волновода).
Рассчитаем в качестве примера параметры эквивалентной схемы плоской нерегулярности в виде скачкообразного изменения размера плоского волновода
(рис. 3).
Рис. 3.
Определим значение проводимости Yш = g +ib , учитывающей краевой эффект от соединения двух линий с различным сечением:
|
|
a |
|
∞ |
Am sin mπb . |
|
Yш = − |
|
|
∑ |
1 |
||
2 |
|
|
|
|||
|
b Z B |
m=1 mπ |
a |
|||
|
|
0 |
0 |
|
|
|
Задача расчёта Yш сводится, вычислению волновых амплитуд
различных типов полей. Для расчёта этих амплитуд обратимся к граничным условиям в точке z = 0. Сшивание электрических полей в плоскости скачка дает:
|
|
|
|
|
|
|
|
|
|
i |
∞ |
b |
|
nπ |
|
|
|
′ |
′′ |
i |
∞ |
a |
mπ |
|
Z0 |
B0 |
+ |
|
∑γn |
Bn cos |
|
x, |
0 ≤ x ≤ b |
. |
|
|
|
||||||||||||||||
|
|
γm Am cos |
|
x = |
|
|
|
|
|
b |
|
|
|||||
Z0 (A0 |
− A0 )+ |
ωε |
∑m=1 |
a |
|
|
|
ωε n=1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b < x ≤ a |
|
|||
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
||
Умножим обе части этого равенства на cos(lπ a)x , где l = 1, 2, 3, … и, интегри-
a)x , где l = 1, 2, 3, … и, интегри-
руя в пределах от 0 до а, с учётом свойств ортогональности тригонометрических функций будем иметь:
|
i |
|
|
|
b |
|
|
|
i |
∞ |
|
b |
|
|
|
|
|
|
|
|
|
|
|
γla Al |
a = |
Z0 B0 |
∫cos lπ xdx − |
|
∑γbn B0 |
∫cos nπ x cos lπ xdx . |
|
||||||||||||||
|
ωε |
|
|
|
||||||||||||||||||
|
|
2 |
|
0 |
a |
|
|
ωε n=1 |
|
0 |
|
|
b |
|
|
a |
|
|
||||
Отсюда следует, что: |
|
|
sin lπb |
|
sin lπb |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
b |
|
|
|
|
(−1) |
n |
|
|
|
|
|
||||
|
Al = −iωεa |
2Z0 B0 |
a |
− 2 |
|
|
a |
∑γbn |
B0 |
|
|
|
|
|
|
. |
(8) |
|||||
|
lπ |
|
a |
lπ |
|
|
|
|
|
2 |
|
|||||||||||
|
|
|
γl |
|
|
|
|
γl |
n=1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− na |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сшивание магнитных полей в плоскости скачка аналогичным образом позволяет получить:
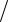
|
∞ |
|
1 |
|
sin mπb |
|
|||||
Bp |
= (−1)p 2a ∑Am |
|
|
|
a |
|
|
. |
(9) |
||
mπ |
|
|
pa |
|
2 |
||||||
|
b m=1 |
|
1 |
|
|
|
|||||
|
|
|
|
− |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
mb |
|
|
|
||
Выражения (8) и (9) представляют собой бесконечные системы линейных алгебраических уравнений, определяющих амплитудные коэффициенты
Am , Bn затухающих полей через коэффициент B0 |
основной волны. |
|
|||||||||||||||||||||||
Подставим далее значения Al |
(при l = m) в выражение для Yш . Это даёт |
||||||||||||||||||||||||
нам следующий результат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2a |
∞ |
sin2 mπa |
|
|
|
|
∞ |
sin2 mπa ∞ |
|
|
|
( |
−1 |
|
n |
|
||||||||
|
|
|
|
|
2a |
|
|
|
|
|
|
B |
b |
|
|
|
|
|
|||||||
Yш = iωε |
|
2 |
∑ |
|
b |
− |
|
|
|
|
∑ |
|
b |
|
∑ |
n |
γn |
|
|
|
|
|
. |
(10) |
|
b |
2 |
2 a |
b |
2 |
|
|
2 |
2 a |
|
|
|
na |
2 |
||||||||||||
|
|
m=1 |
m |
π γm |
|
Z0 m=1 |
m |
π γm |
|
n=1 B |
|
|
−1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ma |
|
|
|
|
|||
Таким образом, для расчёта эквивалентной проводимости необходимо |
|||||||||||||||||||||||||
найти отношения Bn B0 при n = 1, 2, 3, … . С этой целью значения Al |
из урав- |
||||||||||||||||||||||||
нения (8) придётся подставить в уравнение (9). После несложных преобразований будем иметь:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
mπ |
b |
|
|
|
|
|
|
|
|
|
|||||
|
|
Bp |
|
4a |
|
|
|
p |
∞ |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
= iωε |
|
Z0 (−1) |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
||||||
|
|
|
b |
|
|
|
|
|
|
|
a |
|
pa |
2 |
|
|
|
|
|
||||||||||||||
|
|
B0 |
|
|
|
|
|
|
m=1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
π |
γm |
|
|
|
|
|
|
−1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mb |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
4a |
∞ ∞ |
|
b |
|
|
sin2 mπb |
|
|
|
|
|
|
|
|
( |
) |
n |
|
|
|
|||||||||||
|
p |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
−(−1) |
|
∑∑ |
n |
γn |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
. |
(11) |
||||
|
b |
|
|
|
|
|
|
|
pa |
2 |
|
na |
2 |
|
|
|
|||||||||||||||||
|
|
n=1 m=1 |
B0 |
2 |
2 |
|
a |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
m |
π |
|
γm |
|
|
|
|
−1 |
|
|
|
|
|
−1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
mb |
|
|
mb |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Система (11) тоже содержит бесчисленное множество уравнений и бесчисленное множество неизвестных Bp  B0 . Давая индексу p определённые зна-
B0 . Давая индексу p определённые зна-
чения 1, 2, 3, и т.д. и ограничивая число членов уравнений наивысшим значением p, мы получим конечное число уравнений, из которых приближённо можно
определить конечное число неизвестных Bp  B0 .
B0 .
Не останавливаясь на вопросе о возможных преобразованиях для удобства вычислений сумм, входящих в уравнения (11), приведём некоторые конечные результаты.
Анализ показывает, что эквивалентная проводимость Yш имеет ёмкостной характер, т.е. Yш =iωCш , где
