Конспект лекций Электродинамика и РРВ

Наряду с трактовкой точечного заряда как малого физического тела, существует и другая. Объектом теории может быть также идеальный точечный заряд, «заряженная точка». Плотность ρ такого заряда бесконечна в точке его локализации М(r’), а во всех остальных точках пространства равна нулю. Ве-

личину ρ идеального точечного заряда можно выразить при помощи δ-функции Дирака

(6)

Роль пробного тела при исследовании поля может играть не только точечный заряд. В частности, вместо движущегося заряда для индикации магнитного поля может использоваться замкнутый неподвижный виток тока. На плоский замкнутый контур L c током I в магнитном поле действует момент силы К, определяемый следующим образом:

здесь S – площадь, ограниченная контуром L, ν0- орт нормали к поверхности контура, согласованный правовинтовой системой с направлением тока.

Уравнения Максвелла

Уравнения Максвелла заключают в себе основания теории электромагнетизма, и являются постулатами теории.

В комплексной форме операций векторного анализа они записываются следующим образом:

С формальной точки зрения, это дифференциальные уравнения в частных производных относительно компонент векторов Е, Н, D, В, а также j и ρ.

Приведенные формулы (8) – (11) выражают уравнения Максвелла в дифференциальной форме.

Значение уравнений Максвелла как оснований теории электромагнетизма исключительно велико. Для инженера в первую очередь важно, что они, в принципе, дают возможность исследовать любые электромагнитные процессы. Надо лишь уметь правильно ставить соответствующие математические задачи и решать их, привлекая ЭВМ.

Уравнения Максвелла в интегральной форме могут быть получены из (8)

– (11) с использованием теорем Стокса и Остроградского – Гаусса.

Рассмотрим первое из уравнений Максвелла. Поскольку ротор составляется из пространственных производных компонентов вектора, то, как видно из (8), изменения в пространстве магнитного поля (вектор Н слева) связан с изменением электрического поля во времени (вектор D справа).

Пусть сначала изменений во времени нет: процесс стационарен. Тогда

×H = j; ∫H dl = I ,

L

и первое уравнения Максвелла описывает связь магнитного поля с постоянным током.

Если ток проводимости отсутствует (I = 0), но процесс уже не стационарен (происходит изменение во времени), то циркуляция Н, которая в случае постоянного тока была равна I, теперь становится равной величине:

которая называется током смещения. Соответствующая этому функция ∂D∂t

рассматривается как плотность тока смещения.

Отметим, что физическая сущность тока смещения в вакууме никак не связана с движением зарядов.

Назовем величину Iсм + I обобщенным током, а ∂D∂t + j - плотностью

обобщенного тока. В отсутствии магнитного поля Н равен нулю и обобщенный ток. Если обобщенный ток существует, то обязательно присутствует магнитное поле.

Если (×F)= 0 , то из первого уравнения в дифференциальной форме получим:

Отсюда следует, что вектор обобщенного тока не имеет ни источников ни стоков. Его векторные линии, следовательно, замкнуты, или уходят из бесконечности в бесконечность.

Обращаясь ко второму уравнению Максвелла в дифференциальной форме, замечаем, что оно связывает пространственные изменения электрического поля (Е) с изменением во времени магнитного поля. Если электрическое

поле отсутствует Е = 0, то равна нулю вся левая часть (9), откуда ∂B∂t = 0 ,

следовательно, магнитное поле, существующее без электрического, может быть только неизменным во времени, стационарным. При этом всякое изменение магнитного поля ∂B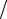∂t ≠ 0 обязательно вызовет появление поля электрическо-

го ( ×E ≠ 0 только при E ≠ 0 ).

Если для потока вектора В через S, называемого магнитным потоком, установить обозначение Ф, а для циркуляции Е по L использовать символ Э, то второе уравнение в интегральной форме принимает вид:

где

Э = ∫E dl; Ф = ∫B dS.

L S

В этой форме второе уравнение Максвелла совпадает с законом электромагнитной индукции Фарадея. Циркуляция Э предстает как электродвижущая сила, наводимая в контуре L изменением магнитного потока Ф.

Однако, закон Фарадея был установлен для проводящих контуров в магнитных полях. Закон электромагнетизма, выражаемый вторым уравнением Максвелла в интегральной форме, значительно шире, поскольку контур L – это любой мысленно очерченный в пространстве контур, причем не имеет значения, какие именно материальные объекты оказались в области построения.

Смысл третьего уравнения в дифференциальной форме прост – линии вектора D начинаются на положительных и заканчиваются на отрицательных зарядах.

Третье уравнение в интегральной форме известно также под названием

теоремы Гаусса.

Четвертое уравнение Максвелла по форме отличается от третьего нулевой правой частью. Это указывает на отсутствие фактора, который можно было бы назвать «магнитным зарядом». Магнитные силовые линии (линии вектора В) обязательно непрерывны, т.е. либо замкнуты, либо идут из бесконечности в бесконечность.

Лекция № 3. Представление материальных сред в электродинамике

Свойства материальных сред

Вмакроскопической электродинамике установлено, что векторы поля D

иВ, а также плотность тока проводимости j связаны с напряженностями поля Е и Н соотношениями, зависящими от свойств среды. Обычно существуют связи:

Если процессы в среде считаются локальными и безынерционными, то функции определяются своими аргументами в той же точке и в тот же момент времени. При этом вместо (1) пишут:

Величины ε и µ называются соответственно относительной диэлектри-

ческой проницаемостью и относительной магнитной проницаемостью, а σ - удельной объемной проводимостью. Полные коэффициенты εа = ε0ε и µа = µ0µ -

абсолютные проницаемости.

Соотношение (1) и все их возможные формы, включая (2) – (4), называ-

ют материальными уравнениями.

Обычно вещество само по себе не создает макроскопически наблюдаемого поля (примеры исключения - постоянные магниты и сегнетоэлектрики). Это объясняется уравновешенностью внутренних процессов в веществе на микроскопическом уровне. В частности, нейтрализованы положительные и отрицательные заряды.

Во внешнем электрическом поле происходит деформация и переориентация молекул и атомов, электрический заряд которых продолжает оставаться связанным в структуре вещества. В результате отклонения зарядов появляется нескомпенсированное внутреннее поле, которое, налагаясь на внешнее, заметно изменяет его. Это называется поляризацией среды. Аналогичный процесс, связанный с магнитным полем, называется намагничиванием.

Пусть некоторое электромагнитное поле в вакууме характеризуется параметрами Е, Н. При этом

Приращения Р и М называют поляризованностью (электрической поляризацией) и, соответственно намагниченностью (магнитной поляризацией).

Процессы поляризации и намагничивания среды выступают как независимые, т.е. первый связан только с электрическим, а второй – только с магнитным полем:

В большинстве случаев этим соотношениям можно придать простую форму:

где безразмерные коэффициенты χэ, χм - это так называемые электрическая и магнитная восприимчивости среды. Они выражают «меру отклика» среды на прилагаемое внешнее поле. Восприимчивости связаны простыми соотношениями с относительными проницаемости:

Третье материальное уравнение устанавливает связь плотности тока проводимости с напряженностью электрического поля:

j = σE.

При σ = const это уравнение воспроизводит физическое содержание закона Ома. В отличие от обычной формулировки этого закона, оно является локальным, т.е. выражает связь физических величин в точке. Удельная проводимость σ имеет размерность [1/ОМ*м]. Она измеряется в сименсах на метр

[См/м].

В теории удобно пользоваться представлениями об идеальном проводнике, как среде с неограниченной проводимостью (σ→ ∞) и об идеальном ди-

электрике, как среде, лишенной проводимости (σ = 0). Рассмотрим различия этих сред с точки зрения электродинамики.

Преобразуем выражение для плотности обобщенного тока с использованием материальных уравнений для некоторой среды с параметрами ε, σ:

(10)

Как видим, в случае идеального диэлектрика здесь исчезает первый член j = σE, а при переходе к идеальному проводнику второй член оказывается бесконечно малым в сравнении с первым (при всякой реальной скорости процесса). Это значит, что в идеальном диэлектрике может существовать только ток смещения, а в идеальном проводнике – только ток проводимости.

Если величина плотности тока смещения значительно превышает величину плотности тока проводимости, то среду относят к диэлектрикам. Если величина плотности тока смещения в среде много меньше величины плотности тока проводимости, то такую среду относят к проводникам. Если оба слагаемых в (10) одного порядка, то такую среду нельзя отнести ни к проводникам, ни к диэлектрикам.

Поскольку величина плотности тока смещения зависит от скорости процесса, то такое деление является условным.

Входящие в материальные уравнения величины ε, µ, σ выступают как

параметры сред.

В большинстве случаев ε, µ, σ могут рассматриваться как скалярные коэффициенты векторов. Это значит, что вектора E и D, Н и В, Е и j коллинеарны, а свойства среды не зависят от направления поля. Среды, характеризуемые скалярными ε, µ, σ называют изотропными.

В тех случаях, когда указанные вектора не коллинеарны, ε, µ, σ являются тензорными величинами, а характеризуемые ими среды называются анизо-

тропными.

Говорят, что среда однородна в области V, если параметры ε, µ, σ (скаляры или тензоры) постоянны в V. Если же их следует рассматривать как функции координат, то среда неоднородна. Кусочно-однородными называют среды, параметры которых принимают различные постоянные значения в разных областях.

В большинстве случаев ε, µ, σ можно считать не зависящими от векторов поля. Материальные уравнения при этом линейны. Линейными называют и соответствующие среды. Нелинейность большинства сред проявляется только в очень сильных полях.

Поля на границах раздела сред

При рассмотрении материального объекта электродинамики мы всегда встречаемся с границами разнородных сред. Такой границей является поверхность всякого физического тела.

С точки зрения макроскопической электродинамики, поверхность раздела сред – это такая поверхность, на которой параметры ε, µ, σ (или хотя бы один из них) терпят разрыв как функции координат.

Рис. 1. К определению граничных условий для полей

Пусть поверхность S разделяет среды 1 и 2. выберем на S точку М и выделим столь малую ее поверхность ∆S, что этот элемент поверхности можно считать плоским. В точке М построим орт нормали х0 (направление – из среды 2 в 1). Построим на ∆S два касательных ортогональных орта τ0 и τ0’. При этом

получаем тройку ортогональных векторов х0, τ0 и τ0’, по которым можно разложить любой из векторов поля Е, Н, В, D в точке М.

Если орт τ0 выбран так, что он совпадает по направлению с проекцией

Говорят, что вектор поля F, разложен на нормальную и тангенциальную (касательную) компоненты.

В ряде случаев на границе раздела сред могут располагаться микроскопические носители заряда, как неподвижные, так и образующие ток проводимости. В макроскопической электродинамике принимается, что такого рода за-

ряды не имеют объема, и являются поверхностными. Плотностью поверхно-

стного заряда называют величину:

Плотностью поверхностного тока в точке М называется величина:

где орт l0 указывает направление тока, ортогональное некоторой линии ∆l. Поскольку ε, µ, σ разрывны, то компоненты векторов поля при переходе

границ раздела тоже будут испытывать разрывы. Тогда векторная линия будет претерпевать излом. В общем случае переход от F1 к F2 на границе происходит с изменением как абсолютной величины, так и направления вектора.

Это равенство означает, что тангенциальная компонента вектора Е при переходе границы раздела всегда остается непрерывной. Второе равенство использовать удобнее, т.к. ν0 выбирается однозначно.

Нормальная компонента вектора магнитной индукции В на границе разрыва всегда непрерывна.

Тангенциальная компонента вектора Н непрерывна только при отсутствии на границе поверхностного тока, а в общем случае справедливо граничное условие:

Рис.2. К определению плотности поверхностного заряда

Поверхностный заряд можно условно представить как объемный, который распределен с плотностью:

где ξ - плотность поверхностного заряда поверхности S, функции координат q1, q2, заданных на этой поверхности; ν – нормальная компонента, принимающая значение ν’ при пересечении S.

V

q 1

?

q 2

S

Рис. 3. К представлению поверхностного заряда плотностью объемного заряда

Аналогично можно рассматривать поверхностный ток, введя плотность

Баланс энергии поля

Поскольку электромагнитное поле физически реально, оно обладает энергией. Выясним, каким образом векторы поля E, D, Н, В определяют его

энергию W.

Умножим второе уравнение Максвелла скалярно на Н, а первое - на Е

H ×E = −H ∂∂Bt ,

E ×H = E ∂∂Bt + E j.

Вычтем второе соотношение из первого

H ×E − E ×H = −H ∂∂Bt − E ∂∂Dt + E j,

и используя формулу векторного анализа, получим:

Проинтегрируем полученное соотношение по некоторому объему V, ограниченному поверхностью S, и применим к левой части теорему Гаусса – Остроградского:

Равенство (23) есть уравнение баланса энергии поля в объеме V.

Введя обозначения

P = ∫j ЕdV - мощность тепловых потерь;

V

Уравнение баланса энергии запишется в виде: