Конспект лекций Электродинамика и РРВ

Полученный результат физически объясняется тем, что рассматриваемая неоднородность создаёт в линии затухающие поля поперечно-магнитного типа. А у таких полей электрическая энергия на единицу длины линии превышает энергию магнитную.

Численные расчёты позволяют установить, что второй член в правой части равенства (12) относительно мал, и поэтому его в большинстве случаев можно не учитывать. Таким образом, в первом приближении

Если размеры сечения достаточно малы по сравнению с λ, то, учитывая, что слагаемые суммы быстро убывают с увеличением m, можно принять

γam= mπ/ a . В этом случае

Рассмотренный метод, естественно, может применяться для расчёта эквивалентных параметров плоских неоднородностей и других типов. При этом в каждом конкретном случае надо составить уравнения непрерывности проекций

E и H , касательных к границе раздела, и найти их решение.

Лекция № 23. Возбуждение волноводов

Рассмотрим методы возбуждения электромагнитных волн в волноводах. Для выяснения условий возбуждения волноводов используем принцип взаимности. Исходя из этого принципа, можно утверждать, что конструкции устройств, предназначенных для возбуждения в волноводе волны определенного типа, или для извлечения энергии из волновода с волной того же типа, долж-

ны быть одинаковыми.

Итак, представим себе, что в волноводе движется волна определенного типа. Каким образом можно извлечь максимальную энергию из этого волновода?

Известны следующие способы решения подобной задачи.

1.В волноводе необходимо поместить прямой провод так, чтобы он находился в точке, где напряженность электрического поля имеет максимальное значение, и ориентировать провод так, чтобы его ось совпадала с направлением напряженности электрического поля. При такой ориентации провода индуцируемая в нем э.д.с. будет максимальна.

2.В волноводе необходимо поместить рамочную антенну (виток), ориентировав ее так, чтобы нормаль к плоскости рамки совпадала с направлением вектора напряженности магнитного поля. При этом рамку сле-

дует расположить там, где нормальная к ее плоскости напряженность магнитного поля имеет максимальное значение.

Приведенные способы обеспечат извлечение из волновода максимальной мощности, если сопротивление нагрузки, кроме того, согласовано с источником энергии (волноводом).

Исходя из вышеизложенного и основываясь на принципе взаимности, приходим к следующим правилам возбуждения в волноводе волны того или иного типа.

1.Необходимо установить структуру поля волны, которую желательно возбудить.

2.Для возбуждения волны в волновод можно поместить проводник или систему проводников с током, расположив их вдоль направления вектора напряженности электрического поля в тех точках, где это поле должно иметь максимальное значение.

3.При возбуждении рамкой последнюю следует поместить в волноводе, там, где напряженность магнитного поля максимальна. Плоскость рамки необходимо ориентировать перпендикулярно силовым линиям

Н.

Возбуждающий элемент создает в волноводе множество полей различных типов. Более того, мы можем утверждать, что возбудить в волноводе поле только одного типа, очевидно, нельзя.

В самом деле, возбуждение поля связано с введением в волновод источника. Значит, поле в волноводе должно удовлетворять граничным условиям не только на стенках волновода, но и в точках где находится источник. Ясно, что

поле одного типа удовлетворить последнему требованию не может. Для этого потребуется совокупность множество типов полей, которые и образуют в волноводе результирующее поле сложной конфигурации.

Если размеры поперечного сечения волновода таковы, что из множества типов полей лишь одно, с наименьшей критической частотой, может распространяться в волноводе, то все остальные поля будут затухающими. Естественно, такие поля в переносе энергии по волноводу не участвуют, ибо они имеют чисто колебательный характер. По мере удаления от источника напряженности затухающих полей убывают. Стало быть, начиная с некоторого расстояния от источника мы будем иметь фактически одну незатухающую волну.

Перейдем теперь к теоретическому анализу возбуждения волноводов. Определение электромагнитного поля в волноводе по заданным источни-

кам сводится к решению системы уравнений Максвелла в области, ограниченной идеально проводящими стенками, при условии, что Еτ на этих стенках равна нулю.

Впервые подобная задача для одного частного случая рассматривалась С.А. Щелкуновым. затем она была решена в общем виде советскими учеными Г.В. Кисунько, А.А. Самарским и Н.Л. Тихоновым и др.

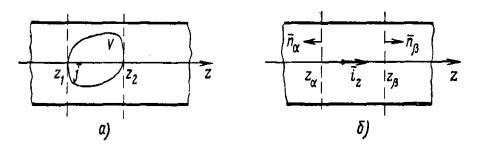
Пусть в бесконечном волноводе источники поля находятся в области V , определенной в интервале z1 ≤ z ≤ z2 (рис.1).

Рис. 1. К расчету поля в волноводе по заданным источникам: а - волновод с источниками в области V; б - волновод с источниками, удаленными на бесконечность

Руководствуясь ранее изложенными соображениями, представим поле в области, где нет токов и зарядов, т.е. слева от плоскости z = z1 и справа от

плоскости z = z2 , в виде совокупности собственных поперечно – электрических

и поперечно – магнитных волн. Совершенно ясно, что справа от плоскости z = z2 волны будут распространяться в положительном направлении оси z , а

слева от плоскости z = z1 - в противоположном, отрицательном направлении. В соответствии с этим для области z ≥ z2 напишем:

Здесь p – индекс, определяющий тип поля в волноводе (в общем случае под p следует понимать два индекса и осуществлять суммирование по обоим

индексам ); E p , H p - комплексные векторы поперечно – электрического или поперечно – магнитного поля p - го типа с амплитудным множителем, равным

единице.

Для областиz ≤ z1 будем иметь:

Знак «минус» здесь обозначает волну, распространяющуюся в отрицательном направлении оси z .

Для определения неизвестных коэффициентов Ap используем лемму Лоренца:

Применим эту лемму к электромагнитному полю в области, ограниченной участком боковой поверхности Sб волновода и плоскостями z = z1 и z = z2 (рис. 1,

а).

Будем считать, что поле E1 , H1 представляет собой искомое электромагнитное поле E, H , возбуждаемое в волноводе заданными источниками, т.е.

E1 = E, H1 = H и i1ст = i ,

В этих выражениях интегралы по поверхности Sб волновода отсутствуют, так

как касательные составляющие вектора E искомого поля и вспомогательных полей здесь равны нулю.

Подставим в выражение (4) значения векторов E и H из равенств (2) и

(3). В результате будем иметь

Прежде чем перейти к преобразованию выражений последнего типа , познакомимся с одним важным свойством собственных полей в волноводе. С этой

целью напишем лемму Лоренца для полей E p , H p и E p' , H p' в области, ограниченной произвольными плоскостями z = zα , z = zβ и участком поверхности

волновода (рис.1, б).

Повторяя рассуждения, аналогичные предыдущим, получим

не должен зависеть от переменной z , ибо сечения S0α и S0β были выбраны произвольно, и, стало быть, равенство (7) справедливо для любых S0α и S0β .

Предположим, что волна с индексом p (т.е. волна p ) распространяется в

Обычно в волноводах различными типами полей соответствуют разные волновые числа. Однако в некоторых случаях это условие нарушается, и волны

даже если p = p' .

Соотношения (8), (9) представляют собой условия ортогональности собственных волн в волноводе.

Будем считать, что волны, движущиеся в отрицательном направлении оси z , имеют отрицательные волновые числа: β− p = −βp . Тогда соотношения (8) и

(9) можно объединить в одно равенство

Анализируя полученные выражения, можно заметить, что продольные токи ( j = jz ) возбуждают в волноводе только поперечно-магнитные волны, т.к. в

этом случае (j E±qTE )= 0 , и, следовательно, (A±q )TE = 0 . Поперечные же токи

будут возбуждать волны обоих типов. Рассмотрение этих выражений подтверждает также и другие качественные выводы относительно способов возбуждения электромагнитных волн.

Применим выражения (11) к расчету электромагнитного поля волны H10 ,

возбуждаемой в прямоугольном волноводе линейным поперечным током, направленным по оси y (рис. 2)

y2

Iвхmhд = ∫I (y)dy .

y1

Подставляя промежуточные результаты в выражения (11) и проведя несложные вычисления, получим