Конспект лекций Электродинамика и РРВ

Лекция № 19. Основная волна прямоугольного волновода

Волнам в классе Н с индексом m = 0 или n = 0 нет соответствия в классе Е; поэтому нет вырождения. Рассматриваемому подклассу принадлежит основная волна Н10.

H10z = H010 cos πax .

На рис. 1 отображен тип поля Н10.

Рис. 1. Распределение поля волны Н10

Отличительным свойством основной волны является однородность поля в направлении y. Структура Н10 играет роль элементарной ячейки при анализе структур Нт0, поле остаётся однородным по y при любых m.

Выпишем формулы, выражающие поле и основные параметры волны

Н10.

E10m = −(iωµ0µχ102 )( H z10 × z0 )e−iГ10 z =

Неидеальность оболочки волновода практически не влияет на структуру волны Н10. Затухание, вносимое металлом реального волновода можно учесть при помощи полученной ранее формулы

S

Сначала выразим мощность, передаваемую волной Н10 при идеальной проводимости оболочки. Пусть также внутренняя среда – идеальный диэлек-

f ≈ fкр10 .

Для подстановки в формулу (4) вычислим погонные потери в проводни-

ке pпm .

Приближенная формула (7) теряет смысл при f = fкр (λ = 2а). Несмотря на это, она вполне пригодна для расчета затухания волны Н10 при частотах, не слишком близких к критической.

Если уменьшать размер b поперечного сечения волновода, то постоянная распространения Г10, а вместе с ней - фазовая скорость основной волны и соответствующая длина волна Λ, групповая скорость и волновое сопротивление Z10H останутся неизменными. Но, как видно из (7), это существенно затронет коэффициент затухания, который при b << a почти обратно пропорционален b.

Круглому волноводу, так же как и прямоугольному, свойственно бесконечное множество свободных электромагнитных полей классов Е и Н. Чтобы выбрать решение, соответствующее классу Е, надо задать порядок n функции Бесселя и номер m корня Bmn уравнения (10). Выбирая решение из класса Н, задают порядок n функции Бесселя и номер m Cmn уравнения (13). Эти решения дают типы полей Emn или Hmn, соответственно. Наименьшим оказывается корень C11 = 1.841… Таким образом, волна H11 обладает наинизшей критической

частотой

Это основная волна круглого волновода.

Неопределенность в F(nα) отражает свободу азимутальной ориентации собственных волн. Если для некоторого типа поля при n ≠ 0 в одном случае взять F(nα) = cos(nα), а в другом F(nα) = sin(nα), то получатся две структуры, различающиеся только поворотом на угол 90o/n. Вообще при вещественных А

и В имеем Acos(nα)+Bsin(nα)=Ccos(nα - ψ), где C = A2 + B2 и ψ = arctg(B A).

Это значит, что по сравнению со случаем B = 0 отмечается поворот структуры на угол ψ/n. Если же взять B = ±iA , то получится структура, вращающаяся относительно оси z, аналог круговой поляризации однородной Т–волны; при этом F (nα) = exp (±inα) На рис.4 представлены картины силовых линий некоторых

типов поля круглого волновода при F(nα) = cos(nα).

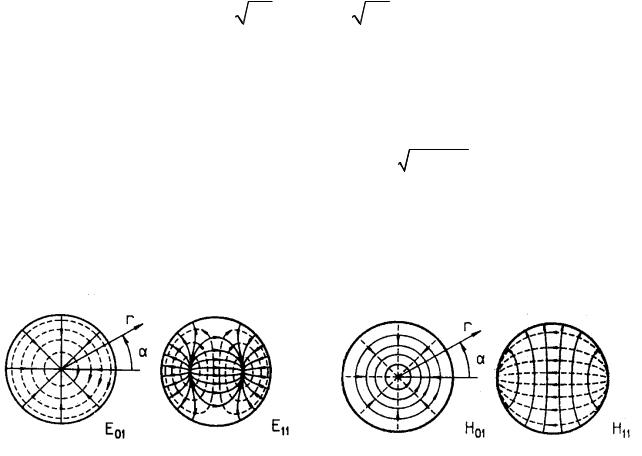
Рис. 4. Структуры полей круглого волновода

Волна Е01 круглого волновода и волна Е11 прямоугольного волновода имеют однотипную структуру; что касается волны Е11 круглого волновода, то она в такой же мере сопоставима с волной Е21 прямоугольного. Но такое соответствие существует только для некоторых видов волн.

Как и в случае прямоугольного волновода, можно выделить ячейки, ограниченные координатными линиями, но уже не ортогональными прямыми, а окружностями и радиальными прямыми. Ячейки будут иметь равные угловые размеры, но окажутся все одинаковыми только при m = 1.

Наиболее интересным свойством этого типа поля (а также всех типов Н0m) является то, что на оболочке волновода (r = R) сохраняется только продольная магнитная компонента Нz, которой соответствует азимутальный ток η = α0Hz. C

ростом частоты или радиуса R отношение Hz/Hr уменьшается, в пределе обращаясь в нуль. Таким образом, могут быть созданы условия, при которых токи в

Уже отмечалось, что волна Н11 - основная. Интересно, что структура её поля и поля основной волны Н10 прямоугольного волновода аналогичны.

Волновые процессы в прямоугольном и круглом волноводах имеют ряд общих черт. Однако волна Н11 круглого волновода в отличие от волны Н10 прямоугольного, как говорят поляризационно неустойчива: небольшие деформации оболочки могут вызвать заметные повороты структуры поля. Это связано с поляризационным вырождением, которое свойственно всем волнам круглого волновода за исключением азимутально-однородных (n = 0).

Лекция № 20. Общая теория электромагнитных резонаторов

Накопление энергии в объеме

Рассматривая ранее различные процессы, мы отмечали, что распространяющиеся, бегущие волны переносят энергию. Вместе с тем было введено представление о стоячей волне, наложении двух противоположно направленных волн с одинаковыми амплитудами; в этом случае (при отсутствии потерь) энергия в среднем не переносится. Если в узлах электрического поля однородной стоячей Т–волны установить идеально проводящие плоскости z = const, прежнее поле сохранится в отсеченном изолированном объеме. Можно сказать, что противоположно направленные бегущие волны полностью отражаются этими плоскостями, на которые они падают по нормали. Движение энергии при этом имеет колебательный характер, как схематически показано на рис. 1а.

Рис.1. Схемы движения энергии в резонаторах

Направление вектора Пойнтинга меняется через четверть периода колебаний поля: он колеблется с удвоенной частотой. Расстояние между соседними плоскостями составляет половину длины волны. Таким образом, условие существования поля между ними выполняется при вполне определенной частоте. Изолированный объем, в котором происходит колебательное движение энергии, в сущности, выступает как ее накопитель. Условие накопления энергии можно реализовать не только при колебательном, но и циклическом движении энергии (рис. 1б) внутри некоторого объема. Поскольку во всех случаях свободные электромагнитные поля в энергетически изолированных объемах могут существовать только при определенных частотах, такие объемы являются резо-

наторами.

Резонатором будет любой отрезок некоторой продольно–однородной структуры, отсеченный двумя поперечными идеально проводящими плоскостями. В отсеченной области возможно существование лишь таких полей, которые в дополнении к граничным условиям, свойственным исходной направляющей структуре, удовлетворяют также условию Еτ = 0 на введенных перегородках. Таким свойством может обладать наложение прямой и обратной волн одного типа. Сосредоточив внимание на поперечной электрической компоненте поля, запишем:

где E t - поперечная проекция вектора E (x, y), а А и В – некоторые комплексные коэффициенты. Потребуем обращения Emt в нуль на плоскости z = 0, что реализуется при В = - А, причем выражение (1) принимает вид

где Emt = −i2A ; это стоячая волна. Налагая такое же условие при z = L, мы должны положить в (2) sinГl = 0 . Отсюда

т.е. постоянная распространения Г не может быть произвольной величиной, а принимает одно значение из этой последовательности. Поскольку Г = 2π/Λ, то из (3) следует

нента вообще отсутствует. Во всех остальных случаях равенство (4) означает, что длина отсеченного отрезка направляющей структуры должна быть кратна половине длины волны (того или иного типа).

Ввиду того, что Г2 = k2 - χ2, получаем

Поскольку k2 = (ω/c)2εµ , то отсюда

Полагая пока ε и µ вещественными константами, будем считать также не зависящим от частоты поперечное волновое число χ (как в случае полых волноводов). Тогда (6) выражает в явной форме частоты, при которых поле может существовать в рассматриваемом объеме. Они называются собственными частотами. Объем выступает таким образом, как резонатор.

Для каждого типа волны в направляющей структуре, которому отвечает определенные χ, существует бесконечное множество собственных частот, получаемых при переборе p. Собственные частоты, соответствующие всем типам волн при всех значениях p, образуют последовательность

0 < ω1 ≤ ω2 ≤…≤ ωn ≤…≤ ∞.

В случае Т–волн χ = 0, так что в соответствии с (6) собственные частоты зависят только от продольного размера L и являются кратными низшей частоты:

Значение р = 0 в данном случае невозможно. Это означало бы полное отсутствие электромагнитного поля: для Т–волн оно чисто поперечное.

Что касается случая p = 0, то поскольку при этом Г = 0, соответствующая собственная частота резонатора, определяемая по формуле (6)

равна критической (круговой) частоте ωкр для данной волны направляющей структуры. Так как при р = 0 поперечное электрическое поле отсутствует, то должно существовать продольное, и следовательно, речь может идти только о Е–волнах. При критической частоте поле не изменяется по z и Λ → ∞. Согласно (4) длина резонатора при этом оказывается неопределенной: L = 0 ∞. Две поперечные плоскости могут располагаться на любом расстоянии друг от друга.

Свойства полей резонаторов

Мы рассмотрели только определенный класс резонаторов, каждый из которых можно трактовать как энергетически изолированный участок направляющей структуры. Их поля обладают свойствами стоячей волны. В простейшем случае векторы Е и Н стоячей волны при отсутствии потерь сдвинуты по фазе на 90о, причем электрическое и магнитное поля синфазны на участке между соседними узлами. Этим свойством отличаются многие поля резонаторов. Из (2) видно, что при вещественных Г и E t поле Еt синфазно в области посто-

янного знака синуса. Пусть Em = Emei ϕE , где фаза ϕЕ не зависит от координат. Определяя комплексную амплитуду Н, имеем:

Н отличается от ϕЕ на π/2. При таком фазовом соотношении наступают моменты, когда существует только электрическое поле или только магнитное. Поток вектора Пойнтинга, проходящий через любое сечение резонатора, в среднем равен нулю. Движение энергии имеет колебательный характер.

Кроме резонаторов на основе продольно однородных структур нередко применяются и другие. Резонатором, например, может быть любая металлическая полость, какое-либо диэлектрическое тело, система зеркал, планарная структура и пр.

В общем случае в теории электромагнитных резонаторов ищутся решения уравнений Максвелла или производных уравнений второго порядка при требуемых граничных условиях. В частности, для произвольного полого резонатора с однородной изотропной средой формулируется одна из следующих

или

ствующие значения ω = ωn - это собственные круговые частоты резонатора, а kn- собственные волновые числа.

Учет потерь. Добротность резонатора

Потери энергии в реальных резонаторах обусловлены поглощением в диэлектрических и металлических элементах, а также в ряде случаев излучением во внешнее пространство (например, полый резонатор излучает при наличии отверстия). Пусть W – запас энергии резонатора при собственных колебаниях некоторого типа с частотой ω, а Рп - мощность потерь. Поскольку рассматривается полная энергия некоторого свободного электромагнитного поля, то уравнение баланса имеет вид

dWdt + Pп = 0.

Введем величину Q = ωW/Pп, которая называется добротностью резонатора. При этом уравнение баланса примет вид

показывает, что запас энергии собственных колебаний экспоненциально падает. Поскольку энергия квадратично связана с полем, то она также экспоненциально затухает, причем амплитуды компонент Е и Н изменяются по закону

в методе комплексных амплитуд комплексной оказывается собственная частота

В большинстве случаев рассматриваются слабо затухающие колебания, для которых ω”<< ω’. Так как при этом локально процесс близок и к периодическому, под Pп в формуле для добротности можно понимать среднюю мощность Pп .