
Конспект лекций Электродинамика и РРВ
.pdf
Ez± = 0; HZ± = 0. |
(9) |
2) Эти векторы ортогональны (взаимно перпендикулярны) |
|
Em± H±m = 0. |
(10) |
3) Отношение скалярных величин Em± и H m± |
равно ± Z (8). |
Если ε и µ - вещественные величины, то среда не поглощает энергию электромагнитного поля. В этом случае вещественными являются волновое число k(z) и волновое сопротивление Z (8).
Будем рассматривать волну, распространяющуюся вдоль оси z:
Em = E+m , Hm = H+m .
Пусть при этом вектор напряженности электрического поля направлен вдоль оси x. Положим
E+m0 = x0 A = x0 Aeiϕ и E−m0 = 0.
тогда
Em = x0 Ae−ikz ; Hm = y0 (A Z )e−ikz . |
(11) |
Переходя от комплексных амплитуд Em и Hm к самим напряженностям |
|
поля E и H , записываем |
|
E = x0 Acos(ωt − kz +ϕ); H = y0 (A Z )cos(ωt − kz + ϕ). |
(12) |
Как видно, векторы поля изменяются по закону плоской однородной гармонической волны, распространяющейся без затухания. Вектор Пойтинга П = E×H направлен по оси z, а следовательно, распространяясь, волна перено-
сит энергию. |
|
|
|
|
Определим скорость переноса энергии. |
Плотность энергии волнового |
|||
поля |
1 |
|
|
|
w = |
(E D + H B)=εε0 A2 cos2 |
(ωt − k z +ϕ), |
(13) |
|
|
2 |
|
|
|
причем плотности электрической и магнитной энергии оказываются равными: wм = wэ = w/2. Далее
П = z0 (A2 Z )cos2 (ωt − k z +ϕ). |
(14) |
Таким образом, получаем следующее выражение скорости передачи энергии волны
vЭ = Пw = z0 Zεε1 0 = z0 c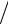 εµ.
εµ.
(15)
Результат показывает, что энергия переносится с фазовой скоростью
волны
v = ω k = с
k = с εµ.
εµ.
Для волны в вакууме (ε = 1, µ = 1) v = c и Z = Z0 Ом.
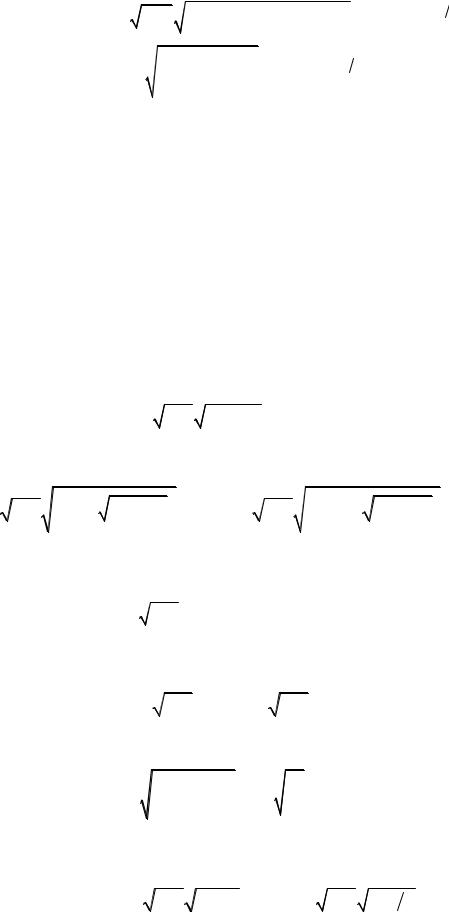
При комплексных ε = ε’(1 - itg∆) и µ = µ’(1 - itg∆м) оказываются также комплексными k и Z.
|
|
|
|
|
ω |
|
|
|
|
|
|
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
k = k |
′ |
−ik |
′′ |
= |
ε'µ' |
|
(1−i tg∆) 1 |
−i tg∆ |
M |
|
= |
k |
e |
−i(∆+∆M ) 2 |
, |
(16) |
||||||||||
с |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
′′ |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z = Z′+ iZ′′ = Z0 |
µ |
(1−itg∆ |
) |
|
|
|
i(∆ |
M |
−∆) 2 |
|
|
|
|
iϕ |
|
|
||||||||||
|
′ |
|
|
= |
Z |
e |
|
|
|
|
= |
Z |
e z . |
|
(17) |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
ε |
(1−itg∆) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если ε’и µ’ положительны, что выполняется всегда за исключением особых случаев, то при положительности ε” и µ”, соответствующей потерям энергии, углы ∆ и ∆M лежат в пределах от 0..900 . Поскольку в этих же пределах лежит и их полусумма, то k’> 0 и k” > 0. Поэтому, переходя от Em и Hm к E и H, теперь получим следующую затухающую волну:
|
|
|
|
|
|
′′ |
|
|
′ |
|
E = x0 Ae |
−k Z |
|
|
|||||||
|
|
|
|
cos(ωt − k z +ϕ), |
|
|||||
|
|
|
A |
|
|
−k′′z |
′ |
(18) |
||
H = y0 |
|
|
|
|
|
e |
|
|
cos(ωt − k z +ϕ− ϕZ ), |
|
|
|
Z |
|
|
|
|
|
|||
|
|
|
|
|
||||||
которая распространяется вдоль оси z с фазовой скоростью v’= ω/k’.
В большинстве практических случаев при рассмотрение электромагнитных волн не приходится учитывать магнитные потери в среде µ” = 0. При этом
k = k0 ε′µ′ |
1−itg∆. |
(19) |
После разделения вещественной и мнимой части имеем |
|
|
k′ = k0 ε′µ′ 12 (1+ 1+ tg2∆); |
k′′ = k0 ε′µ′ 12 (−1+ 1+ tg2∆). |
(20) |
Если tg∆ << 1, т.е. среда – несовершенный диэлектрик, то выражение
(19) можно разложить в ряд
|
|
−i tg∆ |
2 |
∆ |
|
|
k = k0 |
ε′µ′ 1 |
+ tg |
+.... . |
(21) |
||
|
|
2 |
4 |
|
|
|
Отсюда получаются приближенные формулы
′ ′ |
′ ′ |
tg∆ |
. |
(22) |
|
||||
k ' ≈ k0 ε µ ; |
k '' ≈ k0 ε µ |
2 |
||
|
|
|
|
Вычисляя волновое сопротивление, в том же приближении находим
|
|
µ′ |
µ′ |
|
tg∆ |
|
|
Z = Z0 |
|
|
≈ Z0 |
′ 1 |
+ i |
. |
(23) |
′ |
−itg∆) |
||||||
|
ε (1 |
ε |
|
|
2 |
|
|
Пусть теперь tg∆ >> 1: среда – проводник. Пренебрегая в (19) единицей по сравнению с tg∆, напишем
k ≈ k0 ε′µ′ −itg∆ = (1−i)k0 ε′µ′ tg∆ 2 , |
(24) |

т.е.
k′ = k′′ ≈ k0 ε′µ′ tg∆ 2 = |
ωµ0µσ 2 . |
|
|
|
(25) |
||||||
Далее |
|
|
|
|
|
|
|
|
|
|
|
Z = Z0 |
|
|
µ′ |
≈ Z0 |
i |
µ′ |
= (1+ i) |
ωµ |
µ |
. |
(26) |
|
|
|
|
0 |
|
||||||
′ |
(1 |
−itg∆) |
′ |
|
|||||||
|
ε |
|
|
ε tg∆ |
|
2σ |
|
|
|||
Как видим, диэлектрики и проводники резко различаются по характеру распространения электромагнитных волн. Из (22) следует, что затухание в случае диэлектрика очень мало, а коэффициент фазы k’близок к волновому числу при отсутствии потерь. Потери почти не влияют на физическую скорость вол-
ны v= ω/k’.
В случае проводника весьма близкие величины k’и k” велики, т.е. велико затухание и мала длина волны λ = 2π/k’. При переходе к идеальному проводнику (σ → ∞) k’и k” неограниченно возрастают. В частности это означает,
что полное затухание процесса должно происходить на любом конечном расстоянии. Волновое сопротивление (26) и длина волны при σ→∞ стремятся к нулю.
Ввиду (25) пространственное распределение поля распространяющейся в проводнике волны оказывается резко апериодическим. Действительно, на расстоянии
∆0 =1 k '' = 2 ωµ0µσ |
(27) |
амплитуда колебаний уменьшается в e раз, тогда как длина волны λ = 2π/k’
равна величине 2π∆0 . Таким образом, на расстоянии в одну длину волны амплитуда уменьшается в exp(2π) ≈535,5 раз.
Запишем выражение для мгновенного вектора Пойтинга волны в поглощающей среде
|
|
|
A2 |
|
|
|
|
|
′ |
|
|
′ |
|
−2k′′z |
|
||||||
П = z0 |
|
|
|
|
|
|
cos(ωt − k z |
+ϕ)cos(ωt − k z +ϕ−ϕZ )e |
|
= |
|||||||||||
|
Z |
|
|
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
A2 |
|
−2k′′z |
|
|
|
|
|
|
′ |
|
|
|
|
|||||
= z |
|
|
|
|
|
|
|
|
e |
|
cos |
2(ωt − k z |
+ϕ)−ϕ |
+ cos(ϕ ) . |
|||||||
|
2 |
|
Z |
|
|||||||||||||||||
|
0 |
|
|
|
{ |
|
|
|
|
|
z |
|
z |
} |
|||||||
При усреднении во времени получается |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
П = z0 |
A2 |
|
e−2k′′z cos(ϕz ). |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
Z |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Конкретный расчет по формуле (27) показывает, что для металлов на частотах СВЧ диапазона величина ∆0 оказывается весьма малый. Так, для меди, у которой σ = 5.7*107 Cм/м на частоте 10 ГГц (λ0 = 3 cм), имеем ∆0 = 0.6 мкм.

Лекция № 9. Характеристики простейших электромагнитных волн
Поляризация волн
Поляризация волны – это ориентационная характеристика. Плоскость
поляризации, по определению, образована вектором E и направлением распространения волны.
Положив
E+m0 = x0 A + y0 B; E−m0 = 0,
и, определив
H+m0 = Z1 (y0 A − x0 B),
находим общее выражение комплексных амплитуд векторов поля при распространении волны вдоль оси z:
E m+ |
= (x 0 A + y 0 B )e−ikz , |
|||
|
|
1 |
(1) |
|
H m+ |
= |
(x 0 A − y 0 B )e−ikz . |
||
Z |
||||
|
|
|
||
Если начальные фазы компонент вектора Е равны, то ориентация Е при распространении волны не меняется. Волна поляризована в плоскости, составляющей угол
ϑ= arctg(B A)
A)
с плоскостью XOZ. Очевидно, что эту волну можно рассматривать как наложение двух волн с амплитудами A и B, одна из которых поляризована в плоскости XOZ, а другая - в плоскости YOZ.
Рис. 1. Линейная поляризация
Итак, при синфазности декартовых компонент вектора Е распространяющейся волны ориентация поля остается неизменной. Это называется плоской (линейной) поляризацией. Картина оказывается иной, если компоненты поля не синфазны.
Возьмем важный случай, когда амплитуды компонент Ех и Еу одинаковы (A = B), а начальные фазы различаются на 90о. Пусть в (1) A = A eiϕ и

B = A e i ( ϕ ± 9 0 0 ) . Переходя от комплексной амплитуды E+m к напряженности Е+, имеем
E+ = Ae−k '' z [x0 cos(ωt − k ' z + ϕ) ± y0 sin(ωt − k ' z + ϕ)]. |
(2) |
Определяя угол ϑ, указывающий направление плоскости поляризации волны, получаем
tg ϑ = Ey Ex = ±tg(ωt − k ' z +ϕ). |
(3) |
Это значит, что плоскость поляризации не остается фиксированной в пространстве, а вращается. В любой плоскости z = const (например, z = 0) вектор Е, и с ним и все электромагнитное поле волны вращается с угловой частотой ω. Такая поляризация называется круговой. При выборе фазового сдвига - 90о вращение вектора Е должно происходить против часовой стрелки. Это ле-
вая круговая поляризация.
Рис. 2. Круговая поляризация
При фазовом сдвиге 900 (нижний знак в (2) вращение происходит в противоположном направлении – правая круговая поляризация. Зафиксировав некоторый момент времени (t = const), можно получить мгновенный снимок волны круговой поляризации. Он отражает вращательное распределение поля: конец вектора Е будет скользить по винтовой линии.
Рис. 3. Вращательное распределение поля при круговой поляризации

Волна круговой поляризации есть результат наложения двух волн, поляризованных в ортогональных плоскостях, если их амплитуды равны, а фазы сдвинуты на 900 . В общем случае, когда Ех и Еу могут быть не равны по амплитуде и произвольно сдвинуты по фазе, волна имеет эллиптическую поляризацию. При этом вектор Е, вращаясь в плоскости z = const, изменяет свою длину, так что его конец описывает эллипс. Последний оказывается вписанным в прямоугольник со сторонами 2A и 2B.
Рис. 4. Эллиптическая поляризация
Дисперсия, разные оценки скорости распространения
Свойства сред, в которых распространяются реальные электромагнитные процессы, всегда являются в той иной степени частотно-зависимыми. Поэтому должна зависеть от частоты и фазовая скорость электромагнитной волны
v = ω k ' = c Re εµ . |
(4) |
Это называется дисперсией. Заметим, что даже при не зависящих от частоты вещественных проницаемостях ε и µ дисперсия должна существовать в силу присущей средам электропроводности (δ ≠ 0) . Это видно при подстановке
в (4) комплексной диэлектрической проницаемости.
Существование дисперсии необходимо учитывать, оценивая распространение электромагнитных сигналов – волновых процессов, переносящих информацию. Плоская однородная гармоническая волна не может рассматриваться как сигнал. Но такой процесс на самом деле и не может существовать, поскольку, строго говоря, его существование мыслится на бесконечном временном интервале во всем пространстве. Если же он имеет начало и конец, то это – импульс, характеризуемый спектром частот. Сигналы, как известно, всегда обладают некоторым спектром. Поэтому дисперсия влияет ни их распространение. Действительно, представляя сигнал в виде разложения Фурье (необходим интеграл, а не ряд Фурье), мы должны рассматривать распространение гармонических волн, соответствующих всем частотным компонентам. Скорости их распространения различны, ток что, преодолев некоторое расстояние, эти гармонические составляющие приобретут различные фазовые запаздывания. Но сложение с новыми фазовыми сдвигами обязательно приводит к де-
формации, искажению сигнала. Дисперсия может быть мала, тогда она почти не сказывается на распространении сигналов, пока невелики расстояния. Чем она больше, тем более важно учитывать дисперсию.
Рассмотрим напряженность электрического поля сигнала, взяв следующее представление
E = |
∞∫ |
E ( ω) e i [ ω t − k ( ω ) z ] d ω = R e ∞∫ E ( ω) e i[ ω t − k ( ω ) z ] d ω . (5) |
|
−∞ |
0 |
Как видно, при любом z = const компонента вектора Е выражаются интегралами Фурье, а при распространении каждая частотная составляющая приобретает фазовое запаздывание k(ω)z, свойственное плоской однородной волне при этой частоте. Пусть спектр заключен в полосе частот (ω0 - ∆ω, ω0 + ∆ω). Каждой частоте ω можно сопоставить k(ω) и, следовательно, можно говорить, что сигнал характеризуется спектром волновых чисел (k0 - ∆k, k0 + ∆k) , где k0 = k(ω0). Поэтому
ω0 |
+∆ω |
|
|
k0 |
+∆k |
|
|
E = Re |
∫ E(ω)ei[ ωt −k ( ω) z ]d ω = Re |
∫ |
E(k )ei[ ω( k )t −kz ]dk , |
(6) |
|||
ω0 −∆ω |
|
|
k0 −∆k |
|
|
||
где произведена замена переменных ω→ k . |
|
|
|
||||
Разложим частоту как функцию |
волнового числа в ряд Тейлора и огра- |
||||||
ничимся членом с первой производной: |
|
|
|
|
|
||
|
ω ≈ ω + dω |
|
(k − k |
). |
(7) |
||
|
|
||||||
|
0 |
dk |
|
k = k0 |
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
Это представление можно считать оправданным, если дисперсия относительно слаба, а полосы частот и соответствующих им волновых чисел являются узкими. Такой волновой процесс называют группой волн. Внося (7) в (6), получаем
|
( |
|
|
|
k0 |
+∆k |
|
i |
dω |
|
|
|
|
|
|
dk . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E ≈ Re exp i |
ω t − k |
z |
|
∫ |
E(k)exp |
|
|
t − z |
(k − k |
) |
(8) |
||||||
|
0 |
0 |
|
) |
|
|
|
|
k = k0 |
|
|
0 |
|
|
|
||
|
|
|
|
|
k0 |
−∆ |
|
|
dk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||
Пусть E(k) = E(ω) может считаться постоянной величиной (спектраль-
ные компоненты имеют одинаковые амплитуды). Тогда этот множитель выносится за знак интеграла, после чего интеграл легко взять (сделав замену
( k → k − k0 ):
E ≈ Re E(k |
|
) exp i (ω |
t − k |
|
z ) |
k0 +∆k |
||
o |
0 |
∫ |
||||||
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
k0 −∆k |
|
= R e |
E (k0 ) exp [i(ω0 t − k0 z ) ]2 |
|||||||
|
|
|
|
|
(k − k |
|
= |
|
|||||||
exp i d ω |
|
|
t − z |
0 ) dk |
|||
|
dk |
|
k =k0 |
|
|
|
|
|
|
|
|||||
|
d ω |
|
|
|
|
|
||
|
|
|
||||||
sin |
|
|
|
t − z |
∆k |
|
||
dk |
|
|
|
|||||
|
|
k =k0 |
|
|
. |
(9) |
||
|
||||||||
|
|
d ω |
|
|
t − z |
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
dk |
|
k =k0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||

Полагая E(k0 ) = Emeiϕ , окончательно имеем |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
sin dω |
|
|
t − z |
∆k |
|||||||||
E ≈ 2E |
m |
cos(ω t − k |
z +ϕ) |
|
|
|
dk |
|
k =k0 |
|
|
|
|
∆k , |
||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
∆k |
|||||
|
|
|
|
|
|
|
dω |
|
|
|
t − z |
|||||||
где |
|
|
|
|
|
|
|
dk |
|
k =k0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
dω |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
sin |
dk |
t − z ∆k |
|
|
|
|||||||||
|
|
S(z,t) = |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dω |
t |
|
|
|
∆k |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
− z |
|
|
|
|
|
||||||
|
|
|
|
dk |
|
|
|
|
|
|
|
|
|
|
|
|
||
(10)
(11)
есть огибающая гармонической волны, которая, можно сказать, оказалась модулированной.
Рассмотрим мгновенный снимок изучаемой группы волн (рис. 5). Находящаяся внутри огибающей модулированная косинусоида перемещается вдоль оси z с обычной фазовой скоростью v = ω/k.
Рис. 5. Распространение группы волн

Что касается огибающей, то условием поляризации ее максимума является равенство нулю аргумента
ddkωt − z = 0.
Для разных моментов времени t условие выполняется при различных z, т.е. огибающая смещается. Очевидно, что скорость смещения есть
v = |
dω |
. |
(12) |
гр dk
Она называется групповой скоростью.
Соотношение связывает групповую скорость vгр и фазовую скорость v. Отсюда также следует
vгр = v + k |
d ν |
|
d λ |
= v + k |
d ν |
|
d |
|
2π |
= v − λ |
d ν |
. |
(14) |
|
|
|
|
|
|
|
|||||||
d λ |
dk |
d λ |
|
d λ |
|||||||||
|
|
|
|
dk |
k |
|
|
|
|||||
В зависимости от знака производной dv/dk (или dv/dλ) групповая скорость может быть как больше, так и меньше фазовой. Скорость vгр, однако, не может превышать скорости света.
Во всех случаях, когда дисперсия еще не приводит к существенному искажению сигнала, групповая скорость рассматривается как скорость переноса сигнала.
Внося в (12) ω = vk, получаем
v = v + k |
dω |
. |
(13) |
гр dk
Соотношение связывает групповую скорость vгр и фазовую скорость v. Отсюда также следует
vгр = v + k |
d ν |
|
d λ |
= v + k |
d ν |
|
d |
|
2π |
= v − λ |
d ν |
. |
(14) |
|
|
|
|
|
|
|
|
|
|||||||
d λ |
dk |
d λ |
|
k |
d λ |
|||||||||
|
|
|
|
dk |
|
|
|
|
||||||
В зависимости от знака производной dv/dk (или dv/dλ) групповая скорость может быть как больше, так и меньше фазовой. Скорость vгр, однако, не может превышать скорости света.

Лекция № 10. Взаимодействие плоской электромагнитные волны
с границей раздела сред
На практике приходится встречаться с влиянием границ физических тел на распространяющиеся волны, которые испытывают отражение. Это значит, что от границы распространяется новая волна, налагающаяся на первичную. Внутри тела, играющего роль препятствия, также возникает волновой процесс.
Будем рассматривать гармонический волновой процесс в случае, когда все пространство разделено плоскостью на два однородных полупространства с
разными свойствами. Следует найти решения уравнений Максвелла при jст = 0
для каждого из полупространств, удовлетворяющие на указанной плоскости граничным условиям. Эти решения сформируем из плоских однородных волн. В первой среде зададим так называемую падающую волну Е0, Н0, которая распространяется из бесконечности к границе под некоторым углом, и предполо-
жим, что существует отраженная волна Е-, Н-, распространяющаяся от границы. Во второй среде допустим существование одной прошедшей волны Е+, Н+ (ее называют также преломленной волной), которая уходит от границы в бесконечность. Это схематически показано на рис.1.
Рис. 1. Падение волны на плоскую границу раздела
Задача состоит в том, чтобы при заданной падающей волне подобрать такие комплексные амплитуды и направление распространения двух других волн, при которых тангенциальные компоненты векторов Е и Н остаются непрерывными на границе раздела сред.
Запишем это в форме
E0m τ + Em− τ = E+m τ, |
(1) |
|||
H0m τ + Hm− |
τ = Hm+ |
τ. |
||
|
||||
Падающей, отраженной и преломленной волнам сопоставим волновые векторы, указывающие направление распространения плоских волн и по абсолютному значению равные соответствующим волнам числам
