Конспект лекций Электродинамика и РРВ

При использовании проекционных методов представления полей подчиняются системам интегральных соотношений. Производимые при этом опера-

ции называют проецированием.

Большой общностью обладает подход, называемый методом, или процессом Бубнова – Галеркина по имени двух выдающихся инженеров и ученых, наших соотечественников, пришедших к центральной идее в 1913–1915 гг. Непосредственным предметом были задачи технической механики.

Рассмотрим процесс Бубнова – Галеркина, т.е. построение основной проекционной схемы. Поставленную задачу сжато сформулируем в виде равенства:

Здесь – какой-либо оператор задачи, например, дифференциальный (с заданием граничных условий), интегральный или иной; будем полагать его линейным. В правой части – заданная функция f, выражающая обычно то или иное внешнее воздействие на объект. Символом u обозначено неизвестное решение задачи.

Рассмотрим тождественно равную нулю функцию: u − f = 0 . Разлагая ее в ряд Фурье по полной ортогональной системе {un}, мы должны положить

вать базисом процесса Бубнова – Галеркина. Для каждой базисной функции un должно иметь смысл выражение un , т.е. un . Тогда представление u N (4) можно подставить в (3) вместо u. Сохраняя N таких соотношений, имеем:

( uN − f ,uk )= 0 , k = 1, 2, …, N. (5)

Это и есть требование, налагаемое на приближенное решение. В сущности, со-

но, формированию приближенного решения u N (4).

Как видно из (5), при подстановке (4) возникает следующая система линейных алгебраических уравнений:

нородна, то обычно можно построить такую систему {En, Hn}, где каждая пара функций связана уравнениями Максвелла решаемой задачи. При этом неизвестное решение задачи ищем в форме (1); коэффициенты разложений E и H по {En} и {Hn}, соответственно, здесь принципиально одинаковы. Такая сумма удовлетворяет уравнениям задачи при любых коэффициентах cn. Чтобы получить решение некоторой рассматриваемой электродинамической задачи, остается наложить на представление (1) необходимые граничные условия, что приведет к определению коэффициентов cn. При конечном N это, вообще говоря, можно сделать лишь с некоторой точностью.

Процесс наложения граничных условий можно произвести в проекционной форме, т.е. аналогично тому, как в методе Бубнова – Галеркина удовлетворяются уравнения. Такой подход называется методом, или процессом Трефтца. Введенную выше систему решений уравнений Максвелла {En, Hn} будем называть базисом Трефтца, если {En} и {Hn} пригодны для разложения произвольного тангенциального поля на той поверхности, где требуется удовлетворить граничным условиям.

На рис.1 схематически представлено несколько электродинамических задач, для которых естественно применения метода Трефтца.

Все они характерны тем, что область существования поля разделяется на несколько подобластей, в каждой из которых базис Трефтца может быть найден методом разделения переменных.

Базисы Трефтца должны обладать свойством полноты на смежных границах подобластей, где производится проекционное наложение граничных условий непрерывности тангенциальных компонент EN и HN, или, как иногда говорят "проекционное сшивание" представлений поля типа (1). Такой подход называют методом частичных областей; он был впервые применен к задачам электродинамики более полувека назад, но, разумеется, в сколько-нибудь сложных случаях может быть реализован только с применением ЭВМ.

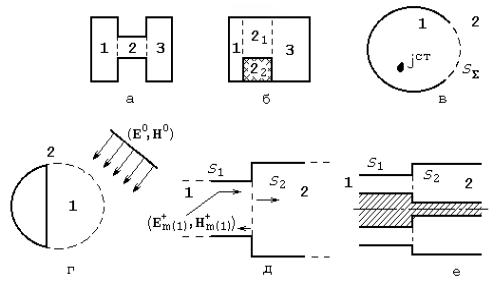
Рис.1

На рис.1 показаны: H-образный волновод (в поперечном сечении) (а); волновод (резонатор) с диэлектрическим включением (б); сферический резонатор, излучающий через отверстие в свободное пространство (в); сферическое зеркало, на которое падает волна (г); два варианта сочленения направляющих структур (д, е). Число таких примеров легко увеличить. Отметим, что в случаях (в) и (г) подобласти одинаковы – шаровая и дополнительная к ней.

Другой важный класс представляют дискретизационные методы. Область, в которой ищут решение, при этом подвергается дискретизации, разбиению. Можно, например, рассматривать решение только на некотором множестве точек, выделенных в области. Образуя разности соседних значений, формируют аналоги производных, так что дифференциальный оператор задачи (например, оператор Лапласа) приближенно заменяется разностным оператором. Такой подход, называемый разностным методом, также сводит задачу к системе линейных алгебраических уравнений. Существуют другие дискретизационные методы, базирующиеся на выделении системы подобластей, а не точек; обычно они имеют черты проекционных.

Реальные технические объекты очень сложны. Поэтому не только сейчас, но и в будущем для большого количества реальных задач прямая алгоритмизация окажется невозможной (или будет требовать неправомерно большого расхода машинного времени), как бы ни был эффективен применяемый проекционный или дискретизационный методы. Выход из положения дает принцип декомпозиции: сложный (протяженный) объект можно расчленить на относительно простые (малые) части. Математические модели строятся для этих частей, причем предусматриваются все мыслимые режимы их взаимодействия. Затем математическая модель исходного сложного объекта получается посредством рекомпозиции, т.е. восстановления из частей при наложении конкретных связей.

Всякой электродинамической структуре можно сопоставить некоторую краевую задачу для уравнений Максвелла, затем в результате алгоритмизации (посредством применения одного из обсуждавшихся выше методов) мыслимо получить математическую модель, реализуемую на ЭВМ. Однако конфигура-

ционная сложность, а также протяженность реальных технических объектов очень быстро ставят предел такому прямому подходу: Не только существующие ЭВМ, но и те, которые ожидаются в обозримом будущем, оказываются недостаточно мощными. Но и относительно простым объектам часто невыгодно сопоставлять краевую задачу, формулируемую для структуры как единого целого. Это ведет к слишком большому расходу машинного времени. Выходом из положения является расчленение структуры на независимо моделируемые час-

ти, автономные блоки. Такой подход называется декомпозиционным.

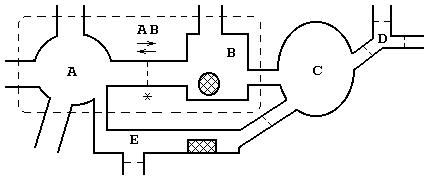
Начнем с рассмотрения простого примера. Чтобы построить математическую модель сложной волноводной структуры, было бы нерационально формулировать краевую задачу для всей области существования поля (рис.2).

Рис.2

Рассечем соединительные волноводы поперечными плоскостями (они показаны штриховыми линиями), в результате чего оказываются выделенными частичные объекты A, B, C, … Алгоритмизировать краевую задачу для каждого такого отдельного объекта гораздо легче. Сосредоточим внимание на объектах A и B. Рассматривая каждый из них с присоединением полубесконечных волноводов, мы можем в результате решения краевых задач определить их матрицы

A B

рассеяния S и S . Таким образом, имеем соотношения:

в которые входят векторы падающих и отраженных волн для объектов A и B.

A B

Порядки матриц S и S вообще различны (nA ≠ nB ); они равны количествам учтенных типов волн. Отмечая, что объекты A и B соединены волноводом (*), в котором учтено k волн, перепишем равенства (8) следующим образом:

Смысл состоит в том, что найдено соотношение между векторами падающих и отраженных волн для того фрагмента волноводной структуры AB, который на

A B

рис.2 заключен в штриховую рамку. Действительно, подвекторы c2± , c2± охва-

тывают падающие и отраженные волны именно для тех волноводов, которые пересекают рамку. Мы получили матрицу рассеяния для фрагмента, представляющего собой объединение объектов A и B и названного AB. Краткая форма записи соотношения (13) имеет вид:

Теперь ясно, как получит матрицу рассеяния всей структуры, которую можно обозначить символом AB…E. Надо принять фрагмент AB за новый объект A, а C за новый объект B и по формулам (14) найти матрицу рассеяния расширенного фрагмента ABC. Затем аналогично присоединяются объекты D и E.

Итак, на первом этапе производится декомпозиция сложной структуры, и находятся матрицы рассеяния полученных ее частей, автономных блоков (они анализируются независимо от того, куда присоединены). На втором этапе выполняется рекомпозиция математической модели полной структуры, т.е. получение ее матрицы рассеяния, по матрицам рассеяния автономных блоков.

Описание автономных блоков при помощи матриц рассеяния охватывает все мыслимые режимы этих блоков, а объединение этих матриц на втором этапе восстанавливает именно те связи, которые реализуются в полной структуре.

Лекция № 31. Общие вопросы распространения радиоволн

1.Классификация радиоволн по диапазонам частот

испособу распространения

Передача сигналов в естественных условиях от передающего устройства к приемному происходит в пространстве, образующем довольно сложную по своим параметрам среду. При распространении радиоволн по таким естественным радиотрассам (радиолиниям) средой служат поверхность и атмосфера Земли или космическое пространство.

Всвободном пространстве радиоволны распространяются прямолинейно со скоростью света с = 3 108 м/с и не испытывают поглощения. Влияние среды на распространение радиоволн проявляется в изменении амплитуды поля волны (большей частью уменьшении), изменении скорости и направления распространения радиоволны, в повороте плоскости поляризации волны, в искажении передаваемых сигналов. Для учета влияния среды на характеристики распространяющихся в ней радиоволн необходимо изучить электрические свойства земной поверхности и атмосферы, а также физические процессы, происходящие при распространении радиоволн.

Условия распространения радиоволн по естественным трассам определяются многими факторами, полный анализ которых оказывается слишком сложным. Поэтому в каждом конкретном случае строят модель трассы распространения радиоволн, выделяя те факторы, которые оказывают основное воздействие, и пренебрегая второстепенными, малосущественными факторами.

Земная поверхность оказывает существенное влияние на распространение радиоволн: в полупроводящей поверхности Земли радиоволны поглощаются; при падении на земную поверхность они отражаются; радиоволны дифрагируют на сферической поверхности земного шара. Радиоволны, распространяющиеся в непосредственной близости (в масштабе длины волны) от поверхности Земли, называют земными радиоволнами. При теоретическом рассмотрении условий распространения земных радиоволн атмосферу обычно, считают сначала непоглощающей средой с относительными диэлектрической и магнитной проницаемостями, равными единице, а затем вносят необходимые поправки.

Вокружающей земной шар атмосфере различают две большие области, отличающиеся своими электрическими свойствами: нейтросферу и ионосферу. Нейтросфера занимает нижний наиболее плотный слой атмосферы толщиной около 60 км. Она состоит из нейтральных молекул атмосферных газов и делится в свою очередь на тропосферу и стратосферу. Тропосфера — приземный слой нейтросферы, простирающийся до высоты примерно 10…15 км. Тропосфера неоднородна как в вертикальном направлении, так и вдоль земной поверхности, кроме того, ее электрические параметры меняются при изменении метеорологических условий. В тропосфере происходит рефракция радиоволн, и поэтому в действительности распространение земных волн зависит от состояния тропосферы. Кроме того, тропосфера обусловливает распространение так

называемых тропосферных волн, которые связаны с явлениями рассеяния и отражения радиоволн от неоднородностей тропосферы.

Стратосфера представляет собой более однородную и менее изменчивую среду. Поскольку плотность газа в атмосфере уменьшается с высотой, относительная диэлектрическая проницаемость в стратосфере близка к единице и эта область оказывает меньшее влияние на распространение радиоволн, чем тропосфера:

Ионосферой называется область атмосферы на высоте 60…20000 км над земной поверхностью. На этих высотах плотность газа весьма мала и газ частично или полностью ионизирован. В этой области число свободных электронов меняется с высотой и составляет 103…106 эл./см2. Присутствие свободных электронов существенно влияет на электрические свойства газа и обусловливает рефракцию и отражение радиоволн в ионосфере. Вследствие рефракции и отражения в ионосфере радиоволны распространяются на очень большие расстояния. Ионосфера является статистически неоднородной средой, и радиоволны рассеиваются в ней, что также обусловливает возможность распространения радиоволн на большие расстояния. Радиоволны, распространяющиеся путем отражения от ионосферы или рассеяния в ней, называют ионосферными волнами. На условия распространения ионосферных волн свойства земной поверхности и тропосферы влияют мало.

На расстояниях в 3…4 радиуса земного шара атмосфера Земли переходит в межпланетную плазму. Газ в межпланетной плазме полностью ионизирован, плотность электронов равна плотности положительно заряженных частиц и составляет 10…100 эл./см3.

Таким образом, оказывается возможным рассмотреть раздельно влияние на распространение радиоволн земной поверхности, тропосферы, ионосферы и межпланетной плазмы.

В связи с полетами космических кораблей к Луне и к ближайшим планетам Солнечной системы (Венере, Марсу) изучаются условия распространения радиоволн в атмосферах и вблизи поверхностей этих планет. Получены данные об электрических параметрах поверхностей планет, строении их атмосфер, что дает основание для построения моделей радиотрасс, проходящих вблизи планет, с использованием опыта работы, наземных радиолиний.

К радиоволнам относят электромагнитные колебания, длина волны ко-

торых лежит в пределах от 2 10-9 до 105 м, что соответствует частотам колебаний от 15 1010 до 3 10-3 МГц.

В зависимости от длины рабочей волны влияние одной и той же среды на распространение радиоволн проявляется по-разному. Радиоволны в зависимости от частоты их колебаний используются на радиолиниях различного назначения. В связи с этим и для удобства выбора модели трассы радиоволны делят на диапазоны (табл.1). Радиоволны каждого диапазона имеют свои особенности распространения, но на границах диапазонов не существует резких изменений этих особенностей.

Диапазон радиоволн ограничен и представляет собой естественный ресурс, который при современном интенсивном развитии радиосредств требует рационального использования. Применение новых путей и средств распространения радиоволн (ретрансляция через искусственные спутники Земли, рассеяние на неоднородностях атмосферы) позволило расширить области использования метровых и более коротких волн. Расширились границы используемых радиоволн как в сторону мириаметровых, так и в сторону миллиметровых волн.

2. Распространение радиоволн в свободном пространстве

Свободное пространство представляет собой неограниченную непоглощающую среду, относительные диэлектрическая и магнитная проницаемости которой равны единице. В действительности таких сред не существует, однако выражения, описывающие условия распространения радиоволн в свободном пространстве, являются фундаментальными. В более сложных случаях обычно пользуются теми же выражениями с внесением в них множителей, учитывающих влияние конкретных условий распространения.

Для проектирования радиосистем различного назначения необходимо уметь рассчитывать напряженность поля вблизи приемной антенны или мощ-

ность сигнала на входе приемного устройства. Протяженность естественных радиотрасс обычно велика (километры - тысячи километров), поэтому всегда рассматривается поле в дальней зоне излучателя. Принято рассчитывать и измерять напряженность электрического поля.

Простейшим излучателем является элементарный электрический вибратор, напряженность электрического поля которого в дальней зоне на расстоянии R от излучателя запишем в виде (индекс θ здесь и далее опускается, индекс 0 указывает, что определяется поле в свободном пространстве):

В ряде случаев напряженность поля удобнее выражать не через ток в антенне, а через мощность, излучаемую антенной. Мощность, излучаемая элементарным вибратором в свободном пространстве, определяется формулой

PΣ = 40 π2 | I0Э | (L/λ)2 [Вт].

Сопоставляя полученные ранее выражения для полей элементарного вибратора в дальней зоне и мощности излучения

получаем формулу для амплитуды напряженности электрического поля элементарного вибратора:

Коэффициент направленного действия — это число, показывающее во сколько раз пришлось бы увеличить мощность излучения антенны при переходе от направленной антенны к ненаправленной при условии сохранения одинаковой напряженности поля в месте приема (при прочих равных условиях): D = PΣнен / PΣ, где PΣнен — мощность излучения ненаправленной антенны.

Элементарный вибратор представляет собой слабонаправленную антенну, его характеристика направленности описывается формулой F (θ)= sin θ и вы-

ражение (1) можно переписать в более общем виде:

Принимая ψЭ = 0, с учетом (1) получаем

Формула (2) справедлива для антенны любого типа, если подставить в нее соответствующие значения D и |F(θ,ϕ)|. На радиолиниях стремятся ориентировать передающие антенны таким образом, чтобы максимум характеристики направленности совпадал с направлением распространения волны на данной радиотрассе (на простейших радиотрассах — это направление на приемную антенну). Поэтому часто принимают |F(θ, ϕ)| = l.

В некоторых случаях определяют не напряженность поля, а мощность в приемной антенне Pпр, которая равна произведению плотности потока энергии П вблизи антенны на эффективную поверхность антенны Аэфф, т. е. площадь