
Конспект лекций Электродинамика и РРВ
.pdf
Проанализируем поле, возбуждаемое элементарным электрическим вибратором.
Расположим начало сферической системы координат в середине вибратора и направим ось z вдоль его оси (рис.2)
Линейный ток на вибраторе по условию представляется выражением
I Э(z) = I0Э = I0Э exp(iψ0 ),
где амплитуда I0Э и фаза ψ0 тока не зависят от z.
Линейное значение объемной плотности тока |
|
jzэст( p,t) = I э(z,t)δ(x −0)δ( y − 0). |
(1) |
Вычислим векторный потенциал |
|
A |
э |
|
|
z |
0 |
|
|
|
э |
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
′ |
|
|
e−ikRpq |
|
′ ′ |
|
′ |
|
|
|
|
|||||||||
|
= |
|
|
|
|
|
I |
|
(z )δ(x |
|
−0)δ( y |
|
|
− |
0) |
|
|
|
|
|
|
dx dy dz |
, |
|
|
(2) |
|||||||||||||||||||
|
|
4πV∫ |
|
|
|
|
|
Rpq |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rpq = |
|
|
|
|
|
′ |
2 |
|
|
|
|
|
|
|
|
|
′ |
|
2 |
|
|
|
|
|
′ |
2 |
= R |
2 |
− 2zz |
′ |
+ z |
′2 |
. |
(3) |
|||||||||||
(x − x ) |
|
|
+ ( y − y ) |
|
+ (z − z ) |
|
|
|
|
||||||||||||||||||||||||||||||||||||
(R - расстояние от начала координат до точки наблюдения). |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Интеграл (2) принимает вид |
Э L 2 |
|
exp(−ikRpq ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
э |
|
|
|
|
|
z |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−L∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
A = 4π I0 |
|
|
|
|
|
Rpq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
dz |
. |
|
|
|
|
|
|
|
(4) |
|||||||||||||||||||||
Магнитное поле диполя H = ×Aэ |
|
определяется в сферической системе |
|||||||||||||||||||||||||||||||||||||||||||
координат с учетом того, что Аэz не зависит от угла ϕ. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r0 |
|
|
|
|
|
|
|
ϑ0 |
|
|
|
|
|
|
ϕ0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
×Aэ |
|
|
|
|
R2 sin θ |
|
|
Rsin θ |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
= |
|
|
|
∂/ ∂R |
|
|
|
|
|
∂/ ∂ϑ |
|
|
∂/ ∂ϕ |
|
|
. |
|
|
|
|
|
|
(5) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aэ |
|
|
|
|
|
|
RAэ |
|
|
|
Rsin ϑAэ |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
ϑ |
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|||
Учтем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aэ |
|
= Aэ r = Aэ(z |
0 |
r ) = Aэ cosϑ, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
z |
|
|
0 |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Aэ |
= Aэ ϑ |
0 |
= Aэ(z |
0 |
ϑ |
|
) = −Aэ sin ϑ, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
0 |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Aэ |
= Aэ ϕ |
0 |
= Aэ(z |
0 |
ϕ |
0 |
) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
HR = 0; |
|
|
Hϑ = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
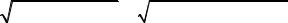
Hϕ = − |
1 ∂ |
(Rsin ϑAzэ )− |
1 ∂ |
(cosϑAzэ ). |
(6) |
|||||
|
|
|
|
|
|
|||||
R ∂R |
R ∂ϑ |
|||||||||
|
|
|
|
|||||||
Вектор напряженности линейного поля имеет только одну составляющую Нϕ, поэтому силовые линии магнитного поля лежат в плоскостях, перпендикулярных прямолинейному излучателю.
Подставив значение Аэz из (4) в (6) и объединив интегралы, получим
|
|
|
|
|
|
|
I э |
|
L / 2 |
|
|
|
|
|
∂ |
|
|
|
|
e−ikRpq |
|
|
∂ |
|
|
|
e−ikRpq |
|||||||||||||||
Hϕ = − |
|
|
|
|
0 |
|
|
|
|
sin ϑ |
|
|
R |
|
|
|
|
+ |
|
|
|
|
|
cosϑ |
|
|
dz′. |
|||||||||||||||
4πR −L∫/ 2 |
∂R |
|
Rpq |
|
∂ϑ |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rpq |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дифференцируя под интегралом, учитывая, что |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
Rpq = |
|
|
|
R2 − 2zz′+ z′2 |
= |
|
|
R2 − 2Rcosϑ+ z′2 ; |
|
|
|
|
|
||||||||||||||||||||||||||||
|
∂Rpq |
= |
|
R − z′cosϑ |
; |
|
|
∂Rpq |
= |
Rz′sin ϑ |
; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
∂R |
|
|
|
|
Rpq |
|
|
|
|
∂ϑ |
|
|
|
Rpq |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂ |
|
|
e−ikRpq |
|
|
|
e−ikRpq |
|
|
|
|
|
|
|
|
|
|
1 |
|
dRpq |
|
|
|
|
|
|
|||||||||||||||
|
|
|
R |
|
|
|
|
|
|
|
= |
|
|
|
|
1 |
− R |
ik + |
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||||
|
|
|
|
|
Rpq |
|
|
|
|
Rpq |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
∂R |
|
|
|
|
|
|
|
|
Rpq |
|
|
|
|
|
|
|
|
|
dR |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d |
|
|
|
|
|
|
e−ikRpq |
|
|
e−ikRpq |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
dRpq |
|
||||||||||||||
|
|
|
cosϑ |
|
|
|
|
|
= |
|
|
|
|
|
−sin ϑ− cosθ ik |
+ |
|
|
|
|
, |
|||||||||||||||||||||
|
|
|
|
Rpq |
|
Rpq |
|
|
Rpq |
|
||||||||||||||||||||||||||||||||
|
dϑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dθ |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
ikR |
|
э |
|
|
L/ 2 e−ikRpq |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
H |
|
|
= |
|
|
|
I |
|
sinϑ |
∫ |
|
R2 |
|
1+ |
|
|
|
|
|
dz′. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
4π |
|
|
|
ikR |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
ϕ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−L/ 2 |
|
|
pq |
|
|
|
pq |
|
|
|
|
|
|
|
|||||||||||
Вектор Е можно найти из соотношения |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
E = −iωµaAэ + |
1 |
|
( Aэ ), |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
iωεа |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
(7)
(8)
но, поскольку магнитное поле представлено всего одной компонентой, проще использовать первое уравнение Максвелла. Если точка наблюдения р находится вне источников ( p V ), то уравнения Максвелла являются однородными, по-
этому
E = |
1 |
×H, p V . |
(9) |
|
|||
|
iωεа |
|
|
Составляющими вектора Е в сферической системе координат являются
ER = |
|
1 |
|
1 |
|
|
∂ |
|
(sin ϑHϕ ); |
|
|||||||
iωεа Rsin ϑ∂ϑ |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||
Eϑ = − |
1 |
|
|
|
1 ∂ |
|
|
RHϕ |
|
; |
(10) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
iωεа R ∂R |
( |
) |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||
Er = 0.

Из выражений (10) следует, что в общем случае вектор напряженности электрического поля прямолинейного излучателя имеет относительно радиальной координаты R продольную составляющую ЕR и поперечную составляющую Eϑ. Поэтому силовые линии электрического поля лежат в меридиональных плоскостях.
На практике особый интерес представляет знание поля на очень больших расстояниях от излучателя, таких, что R→∞(R L). Эту область простран-
ства называют дальней зоной или зоной излучателя.
Рассмотрим выражение для составляющей HR в дальней зоне. Расстояние Rpq между точкой интегрирования q и точкой наблюдения р в этом случае
|
|
′ |
|
′ |
|
2 |
|
|
||
Rpq = R |
|
z |
|
z |
′ |
(R →∞). |
|
|||
1−2 |
|
|
cosϑ+ |
|
|
|
(11) |
|||
R |
≈≈ R −z cosϑ |
|||||||||
|
|
R |
|
|
|
|
||||
Для множителя в подынтегральном выражении (7) получаем
R |
e−ikRpq |
|
1 |
|
|
e−ikR |
e |
ikz′cos ϑ |
|
. |
(12) |
||
|
|
|
|||||||||||
2 |
1 |
+ |
|
|
≈ |
|
|
|
|||||
|
|
|
|||||||||||
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
Rpq |
|
|
ikRpq |
|
|
|
|
k |
R→∞ |
|
||
|
|
|
|
|
|
|
|
||||||
Таким образом, в дальней зоне выражение (7) имеет вид
Hϕ = |
ik |
I0э sin ϑe−ikR |
L∫/ 2 |
eikz′cos ϑdz′ ≈ |
ik |
I0э |
e−ikR |
F (ϑ). |
(13) |
|
4π |
4π |
R |
||||||||
|
R |
−L / 2 |
|
|
|
|
где F(ϑ) - величина, характеризующая зависимость напряженности поля от угла
ϑ.
Теперь можно найти выражения составляющих вектора E. Подставив Hϕ из (13) в (10), получаем при k R → ∞
|
|
|
|
E = |
1 |
|
|
ik |
|
Iэ |
|
e−ikR |
|
|
1 |
|
|
∂ |
sinϑF |
ϑ |
; |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
Rsinϑ |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
R |
iωε |
|
4π 0 |
|
|
|
|
|
|
|
∂ϑ |
( |
|
|
) |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14) |
|||
|
|
|
|
|
1 |
|
|
|
|
|
ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
э |
|
|
|
|
−ikR |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
Eϑ =− |
|
|
|
|
|
|
|
|
|
I0 (−ik) e |
|
F(ϑ)= |
|
|
|
|
|
Hϕ =ZHϕ. |
|||||||||||||||||||||||
iωε |
|
|
4πR |
|
ωε |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|||||
|
|
|
|
Из этих выражений видно, что отношение модулей |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ER |
|
|
|
1 |
|
|
|
|
|
∂ sinϑF(ϑ) /∂ϑ |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
при |
|
|
|
|
|
|
|
|
|
Eϑ |
|
|
|
k |
|
R |
|
|
|
|
|
sinϑF(ϑ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
k |
|
R →∞убывает с ростом расстояния как 1 k R . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
Поэтому в дальней зоне |
|
|
|
Eϕ |
|
|
|
по сравнению с |
|
Eϑ |
|
является очень малой |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величиной. Обычно значением Eϕ пренебрегают.
Поперечные составляющие векторов поля от ϑ зависят по закону F(ϑ), который как видно из формулы (13), определяется функцией распределения линейного тока по излучателю, длиной излучателя и коэффициентом распростра-
нения. Функцию F(ϑ) называют характеристикой направленности излучателя.
В общем случае F(ϑ) - комплексная величина |
F (ϑ)= |
|
F (ϑ) |
|
exp iarg F (ϑ) . |
|
|
|
|||||
|
|
|
|
|
|
|
Функцию F(ϑ) и argF(ϑ) называют амплитудной и фазовой характеристиками направленности, а их графические изображения амплитудной и фазовой диаграммами направленности.
Чем меньше длина излучателя, тем меньше k L и тем меньше меняется в фиксированной точке наблюдаемая величина kRpq в (7) при изменении z’, а
значит и подынтегральная функция. Применяя при |
k |
L 1 теорему о среднем, |
||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
H ϕ ≈ |
ikI эL |
sin ϑ |
e−ikR |
|
+ |
|
|
1 |
|
|||
4 |
0 |
R |
|
1 |
|
|
|
. |
(15) |
|||
|
|
|
||||||||||
|
π |
|
|
|
|
|
ikR |
|
||||
Это выражение является точным в пределе, когда k L → 0. Но при этом электрический момент вибратора I0эL должен оставаться постоянным. Линейный вибратор при этом превращается в точечный вибратор, ток которого можно представить с помощью δ-функции: I э (z )= I0эLδ(z − 0). Для точечного вибратора выражение (15) является точным. В дальней зоне
H ϕ = |
ikI0э L |
|
e −ikR |
|
4π |
sin ϑ |
R , |
(16) |
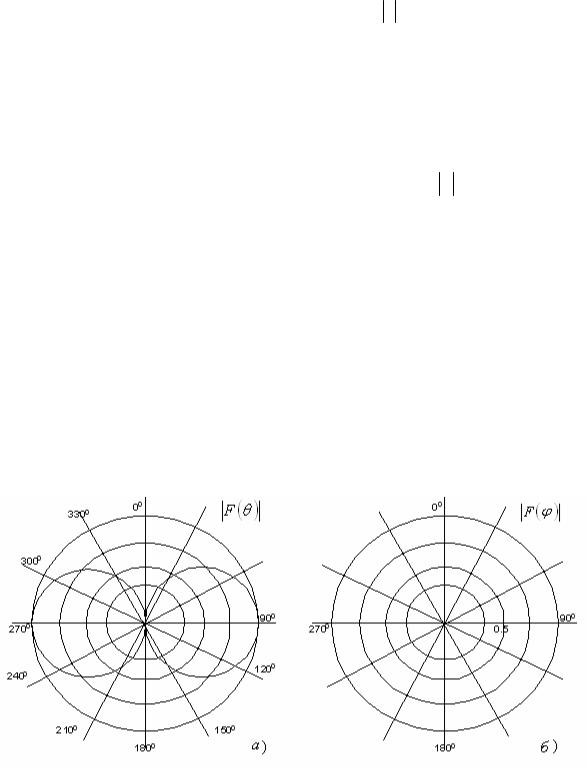
характеристикой направленности элементарного электрического вибратора является выражение F(ϑ) = sinϑ, показывающее, что вибратор вдоль своей оси не излучает.
Амплитудные диаграммы направленности вибратора представлены на
рис. 3
Рис. 3. Амплитудные диаграммы направленности вибратора
Для среднего значения вектора Пойнтинга в дальней зоне имеем
Пср = |
1 Re(E×H )=r0 |
|
1 Z |
|
Hϕ |
|
2 . |
(17) |
|
|
|||||||
|
2 |
|
2 |
|
|
|
|
|
Если вибратор расположен в свободном пространстве (εa = ε0, µa = µ0), то мощность стороннего источника, подведенная к вибратору, расходуется на соз-
дание поля излучения и называется мощностью излучения Р∑ =∫Пср dS. В каче-
s
стве поверхности S выбираем поверхность любой сферы с таким радиусом ρ, чтобы S проходила в зоне излучения. Тогда
π |
2π 1 |
|
|
Hϕ (ρ) |
|
2 2 |
π |
|
э |
|
2 |
|
L 2 |
|
||
|
|
|
|
|
|
|
||||||||||
Р∑ = ∫dϑ∫ |
|
Z |
|
|
ρ sinϑdr = |
|
|
I0 |
|
|
Z |
|
. |
(18) |
||
|
|
|
|
|
|
|
|
|||||||||
0 |
0 |
2 |
|
|
|
|
3 |
|
|
|
|
|
λ |
|
||
|
|
|
|
|
|
|
|
|
||||||||
Вибратор для стороннего источника представляет нагрузку, в которой расходуется мощность PΣ. Сопротивление нагрузки, называемое сопротивлением излучения элементарного электрического вибратора, определяем из соотношения
1 |
|
I |
э |
|
2 |
R |
= |
π |
|
I |
э |
|
2 |
Z |
L 2 |
, откуда R |
|
= |
2π |
Z |
|
L 2 |
. |
(19) |
|||
|
|
|
|
|
|||||||||||||||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
∑ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
∑ |
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
λ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При L λ 1 сопротивление излучателя является малой величиной.
λ 1 сопротивление излучателя является малой величиной.
Лекция № 27. Интегральные соотношения для полей при наличии
поверхности раздела сред
При наличии поверхности раздела сред возникают следующие процессы: сторонние источники возбуждают в пространстве электромагнитное поле, которое, распространяясь по всем направлениям, достигает поверхности, ограничивающей заданный объем, и отражаются (рассеиваются) ею. При этом возникают волны, распространяющиеся в направлениях, обратных направлениям волн, бегущих от источников. В результате переотражений от поверхности раздела в объеме устанавливается некоторое результирующие поле. Физический процесс можно трактовать следующим образом. На поверхности раздела сред под воздействием первичного поля источников могут протекать вторичные поверхностные токи, которые, в свою очередь, возбуждают вторичное поле в объеме. Значения вторичных поверхностных токов должно зависеть от сторонних источников, от параметров среды, формы и граничных условий на самой поверхности раздела.
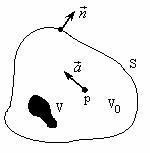
Пусть в объеме V0, ограниченном поверхностью S, задан в области V сторонний ток jст частоты ω, возбуждающей электромагнитное поле напряженности которого Е(p), H(p) надо определить, причем p V0 (рис.1). На поверхно-
сти S удовлетворяются заданные граничные условия. Для решения задачи используем лемму Лоренца
∫(E1 ×H2 − E2 ×H1 ) dS = ∫j1ст (q)E2 (q)dVq − ∫jст2 (q)E1 (q)dVq . |
(1) |
||
S |
V1 |
V2 |
|
|
|
|
|
Рис. 1. К постановке внутренней электродинамической задачи
Примем j1ст = jст. Тогда Е1 = Е(р), Н1 = Н(р). Для того чтобы выразить напряженность электрического поля, введем в рассмотрение в точке р вспомогательный электрический диполь с единичным моментом (IL = 1), ток которого изменяется с той же частотой ω; диполь ориентируем вдоль единичного вектора а. Вспомогательный ток
jст2 = aδ(q − p). |
(2) |
тогда Е2 = Еэ(р,q), Н2 = Нэ(р,q), где q – произвольная точка, |
q V0 ; Еэ(р,q), |
Нэ(р,q) - возбуждаемые в точке q напряженности электрического и магнитного полей вспомогательного электрического диполя, расположенного в точке p.
Подставим значения токов и полей в выражение (1). Точка q является точкой наблюдения тока j2ст, поэтому при подставлении этого тока в интеграл по области V2 по координатам этой точки производится интегрирование. Используя основное свойство δ-функции во втором интеграле правой части и перенеся скалярное произведение аЕ в левую часть равенства, а поверхностный интеграл – в правую, получаем
a E(p) = ∫j |
(q)E |
(p,q)dVq + ∫ E |
(p,q)×H(q)−E(q)×H |
|
(p,q) dSq . (3) |
|
ст |
Э |
|
э |
|
э |
|
V |
|
S |
|
|
|
|
Скалярное произведение аЕ позволяет определить любую составляющую вектора Е. Полагая, например, в сферической системе координат а равным, одному из ортов r0, ϑ0 или ϕ0, найдем составляющие Er, Eϑ или Eϕ. Естественно, что при этом электрический диполь в каждом случае ориентирован или вдоль орта r0, или ϑ0, или ϕ0. Поэтому каждому значению a соответствует свое вспомогательное поле Еэ, Нэ.
Будем считать, что Еэ, Нэ - поле вспомогательного диполя в неограниченном пространстве. Для однородного изотропного пространства это поле определенно на предыдущей лекции. Для неоднородного неограниченного пространства задача определения вспомогательных полей не всегда разрешима.
В выражении (3) интегрирование по объему при известных вспомогательных полях всегда может быть выполнено, так как сторонние токи являются заданными функциями координат. При этом в результате интегрирования получаем некоторую функцию от р. Переставив множители в смешанных произведениях векторов, поверхностный интеграл в последнем равенстве целесообразно представить в следующем виде
|
э |
|
э |
|
|
э |
|
э |
(4) |
∫ E |
(p,q)×H(q)−E(q)×H |
(q, p) |
ndSq = ∫ (H×n) E |
−(n×E) H dSq . |
|||||
S |
|
|
|
|
S |
|
|
|
|
|
Поскольку |
выражения |
(H ×n) и (n ×E) |
определяют |
касательные |
со- |
|||
ставляющие векторов искомых полей на поверхности, то из выражения (3) следует, что касательные составляющие векторов искомого поля входят под знаки поверхностных интегралов и для того, чтобы найти искомое поле в произвольной точке p V0 , надо знать касательные составляющие векторов того же ис-
комого поля на ограничивающей поверхности S. В некоторых важных задачах электродинамики касательные составляющие векторов напряженности искомых полей на поверхностях S могут быть заданы с помощью приближенных представлений: на основе опытных данных, (на основе измерений) или вычислении путем приближенного решения задачи. Тогда в результате интегрирования по поверхности S получим некоторую функцию от р. Значит, вектор Е становится известной функцией. Другой вектор (Н) находится из уравнений Максвелла.
Если точку наблюдения р расположить надлежащим образом на поверхности S и определить составляющую вектора Е, касательную к поверхности, то из выражения (3) найдем, что искомая касательная составляющая вектора входит и под интеграл в правой части равенства. Таким образом получается инте-
гральное уравнение относительно неизвестной касательной составляющей вектора поля.
Введем в рассмотренные эквивалентные поверхностные токи.
H ×n = jэ, |
n ×E = jм . |
(5) |
При этом из выражения (3) получаем |
|
|
a E(p) = ∫jст EэdVq + ∫(jэ Eэ − jм Hэ )dSq , p V0 . |
(6) |
|
V |
S |
|
Из этого выражения видно, что эквивалентные поверхностные токи в возбуждении поля играют ту же роль, что и сторонний ток. Но существенно то, что сторонние токи являются заданными функциями, а эквивалентные поверхностные токи появляются под воздействием полей сторонних токов.
Очень часто при решении практически важных задач электродинамики применяют теорему эквивалентных поверхностных токов. Для того чтобы по-
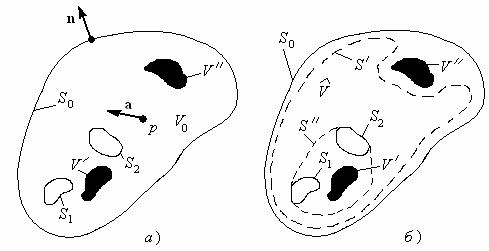
лучить исходные выражения, применяемые при этом для расчета векторов напряженности поля, и сформулировать теорему, предположим, что необходимо решить такую электродинамическую задачу, в которой заданы изолированные замкнутые поверхности S0, S1, S2 (может быть и ряд других поверхностей). Источники поля заданны в объемах V’ и V”, расположенных в общем случае на разных расстояниях от начала координат (рис.2, начало координат находится внутри объема V0).
Рис. 2. К доказательству теоремы эквивалентности
В формуле (6) интеграл распространяется по поверхности S0, S1, S2, обычно имеющим в реальных условиях сложную форму. Чем сложнее поверхности, тем сложнее процедура вычисления поля. Поэтому с целью упрощения вычислений применим следующий прием. Введем в рассмотрение некоторые
фиктивные поверхности S’ и S” так, чтобы в объеме ˆ , ограниченном поверх-
V
ностями S’ и S”, не оказалось сторонних источников поля (рис. 2б). Поверхности S’ и S” могут совпадать с S0, S1, S2, выбор их формы определяется стремлением возможно больше упростить решение поставленной задачи. Считаем,
ˆ |
ˆ |
что точка наблюдения находится в объеме V |
(p V ), в котором сторонних ис- |
ˆ
точников нет. Значит, уравнения Максвелла в области V являются однородными, поэтому в исходном выражении (6) объемный интеграл отсутствует, а поверхностный интеграл берется по S’ и S”. С учетом этого получаем
э |
E |
э |
м |
э |
)dSq , |
ˆ |
(7) |
a E(p) = ∫ (j |
|
− j |
H |
p V . |
S '+S ''
Из выражения (7) следует, что электромагнитное поле в объеме, в котором отсутствуют сторонние токи, возбуждаются распределенными на ограничивающих объем поверхностях эквивалентными поверхностными токами. Если
ˆ
электромагнитное поле вне объема V можно каким либо методом найти, то тем самым определяется и касательные к поверхности составляющие векторов поля. По касательным составляющим с помощью выражений (5) вычисляют эквивалентные поверхностные токи.
Теорема эквивалентных поверхностных токов гласит: поле в свободной от источников области может быть создано электрическими и магнитными токами, распределенными по ограничивающей область поверхности, а в этом смысле действительные источники поля можно заменить «эквивалентными» поверхностными токами.
При вычислении составляющих векторов напряженности электрического и магнитного полей иногда используется интеграл Кирхгофа, количественно выражающий принцип Гюйгенса.
ˆ
Рассмотрим свободную от сторонних источников область V , ограниченную поверхностями S’ и S” (рис. 2б). Найдем интегральные выражения состав-
ˆ
ляющих векторов поля Е и Н в области V .
ˆ
Уравнения Максвелла в области V являются однородными, следовательно, уравнения Гельмгольца тоже являются однородными и для любой декартовой составляющей векторов поля (Еi и Hi) имеем
|
2 |
2 |
Ei =0, |
2 |
2 |
Hi =0, |
ˆ |
, |
(8) |
|
где i = x, y, z. |
Ei +k |
|
Hi +k |
p V |
||||||
ˆ |
|
|
|
|
|
|
|
|
||
Пусть в точке |
расположен точечный источник. |
Скалярное поле |
||||||||
q V |
||||||||||
этого источника является функцией Грина G(p,q), удовлетворяющей уравнению
2G + k2G = −δ( p − q). |
(9) |
Умножим последнее уравнение, например, на Еi, а предыдущее (для Еi) – на G и вычтем первый результат из второго. Интегрируя полученное равенство
ˆ |
|
|
|
|
|
по области V и применяя основное свойство δ-функции, получаем |
|
||||
|
|
|
ˆ |
, |
|
|
|
Ei (q),q V1 |
(10) |
||
∫(G 2 Ei − Ei 2G)dV = ∫Eiδ(p − q)dV = |
ˆ |
|
|||
ˆ |
ˆ |
0, |
|
|
|
V |
V |
q V . |
|
||
|
|
|
1 |
|
|

2 |
2 |
G)dV = |
∫ |
|
∂E |
∂G |
∫(G |
Ei − Ei |
G |
i − Ei |
i dS , |
||
ˆ |
|
|
S '+S '' |
|
∂n |
∂n |
V |
|
|
|
|
|
и меняя местами координаты точек р и q, имеем
Ei (p)= ∫ |
|
∂Ei (q) |
G (p,q)− E (q) |
∂G (p,q) |
ˆ |
|
|
∂n |
∂n |
dSq , |
p V . |
||
S '+S '' |
|
|
|
|||
Если поверхность S” отодвинута на бесконечность, то применяя условия изменения, имеем
Ei (p)= |
∂Ei |
G − Ei |
∂G |
ˆ |
(11) |
|
|
∂n |
dSq , |
p V . |
|||
|
S∫' |
|
∂n |
|
|
|
В качестве функции G здесь может быть использована функция Грина неограниченного однородного трехмерного пространства
1 e−ikRpq
G(p,q)= 4π Rpq .
Выражение (11) позволяет по известным значениям Еi, и дЕi/дп на граничной поверхности определить функцию Еi во всех точках объема.
Следует иметь в виду, что задавать произвольно, не связанные друг с другом значения составляющих векторов поля и их нормальных производных производных на границе нельзя, так как эти значения строго связаны интегральным равенством, получающимся из (11), если точку р расположить на поверхности S’. Поэтому при приближенных вычислениях необходимо задавать составляющие поля и их нормальные производные, наиболее удовлетворяющие интегральному равенству при p S'.
Выражение (11) называют интегралом Кирхгофа. Оно дает количественную формулировку принципа Гюйгенса, согласно которому функция Еi, характеризующая интенсивность волнового процесса (удовлетворяющая скалярному уравнению Гельмгольца), в любой точке наблюдения является суперпозицией сферических волн, излучаемых элементарными источниками, распределенными на заданной поверхности (в частном случае являющейся поверхностью волнового фронта).
Если сравнивать интеграл Кирхгофа с выражением (7), учитывающим векторный характер поля, то можно сделать такой качественный вывод: составляющая вектора напряженности поля и ее нормальная производная на границе играют роль эквивалентных поверхностных токов; вспомогательные поля Еэ, Нэ играют роль функции Грина и ее нормальной производной. С помощью поверхностного интеграла в (7) или в (11) производится суммирование излучения элементарных источников, распределенных на ограничивающей объем поверхности. Функция Грина, описывающая излучение точечного источника, количественно характеризует поле распределенных на поверхности элементарных излучателей.
