1.Федоров Н.Н. Основы электродинамики. – М.: Высш. шк., 1980.

2.Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.

3.Гольдштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны. – М.: Сов. радио, 1971.

Лекция № 1. Введение. Исходные математические понятия

Воснове теории электродинамики лежит представление об электромагнитном (ЭМ) поле. Формально об ЭМ поле можно говорить как о поле сил, т.е. Если в пространство, где существует ЭМ поле, поместить единичный положительный точечный заряд, то на него будут действовать силы.

Вфизическом смысле ЭМ поле следует рассматривать как одну из форм существования материи.

Хотя проявление ЭМ сил в природе люди наблюдали с древних времен, научные понятия в этой области сложились приблизительно недавно.

Вформировании теории ЭМ полей вклад внесли такие ученые, как Шарль Кулон, Майкл Фарадей, Генрих Герц, Александр Степанович Попов, Петр Николаевич Лебедев (измерил световое давление).

Исключительный вклад в науку было суждено внести Максвеллу. В современной физике уравнения Максвелла являются фундаментальными законами теории электромагнетизма. Максвеллу принадлежит теоретический вывод о существовании электромагнитных волн вместе с гипотезой об электромаг-

нитной природе света. Этот вклад является результатом анализа, отправной точкой которого были физические идеи Фарадея (принцип близкодействия – взаимодействие, осуществляющееся через среду, являющуюся «вместилищем» электромагнитного процесса).

Широчайшей опытной базой теории электромагнетизма, основывающейся на уравнениях Максвелла, а так же стимулятором ее дальнейшего развития стала радиотехника. Вместе с радиотехникой появилось понятие радиоволны, т.е. электромагнитных волн в радиосистемах.

Важным научным направлением стало исследование распространения радиоволн в природных условиях – над Землей и в космосе. Проблема излучения и приема электромагнитной энергии, переносимой радиоволнами, привела

ктеории антенн.

Под классической (неквантовой) электродинамикой понимают теорию поведения электромагнитного поля, осуществляющего взаимодействие между электрическими зарядами.

Исходные математические понятия

Формально поле определяют заданием в каждой точке рассматриваемой части пространства некоторой скалярной или векторной величины (скалярные и векторные поля).

Скалярное поле, характеризуемое функцией ψ(x,y,z), можно наглядно отобразить при помощи семейства поверхностей уровня

ψ(x,y,z) = Сi

где Сi – константа

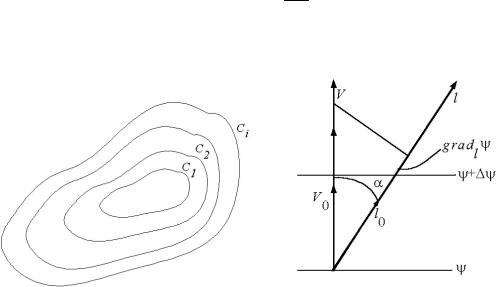
Введем вектор grad ψ, называемый градиентом, который направлен в сторону максимального возрастания ψ и равный скорости изменения ψ в данном направлении. Очевидно, что

grad ψ = ν0 ∂∂νψ ,

где ν – линия, ортогональная к поверхности уровня, а ν0 - касательный к ней орт.

Рис. 1. К определению градиента функции

Проекция вектора grad ψ на некоторое направление l, есть l0 grad ψ = l0 ν0 ∂∂νψ = cosα ∂ψ∂ν = gradl ψ = ∂ψ∂l .

Определяя по этой формуле проекции градиента ψ в декартовой системе координат, получаем

grad ψ = ψ = x0 ∂∂ψx + y0 ∂∂ψy + z0 ∂∂ψz .

Мы видим, что скалярное поле ψ порождает векторное поле F = ψ. Такое векторное поле называется потенциальным, а скалярная функция ψ - по-

тенциалом.

Поверхности уровня, на которой ψ = const являются эквипотенциальными поверхностями.

Для наглядного отображения векторных полей обычно строят картины т.н. векторных, или силовых линий. Это линии, касательные к которым в каждой точке указывают направление вектора. Густота силовых линий может соответствовать интенсивности поля. При этом количество векторных линий, проходящих через ортогональную площадку, должно быть пропорционально абсолютному значению вектора, практически постоянному в пределах площадки.

Векторный дифференциал длины вдоль некоторой линии l – это вектор, направленный по касательной к их абсолютному значению, равный скалярному дифференциалу dl.

Рис. 2. К определению векторного дифференциала длины

В декартовых координатах

dl = τ0dl = x0dx + y0dy + z0dz .

Пусть дано векторное поле ν(x,y,z), которое надо описать посредством векторных линий.

ν = x0νx + y0νy + z0νz .

Попробуем, чтобы выполнялось условие пропорциональности dl = kν,

где k – любая константа.

Приравнивая компоненты векторов ν и dl , получим

Это – система двух дифференциальных уравнений, интегрирование которых приводит к уравнению векторных линий.

Рис. 3. Примеры картин силовых линий

Рассмотрим несколько характерных типов картин силовых линий, которые могут встретиться при исследовании векторного поля F в области V с граничной поверхностью S.

Область V может содержать точку, из которой расходятся силовые линии (исток) или в которую сходятся все силовые линии (сток). Силовые линии могут также проходить область насквозь или совсем не пересекать поверхность

S.

Потоком вектора F через поверхность S (не обязательно замкнутую) называется интеграл:

Ф = ∫F ds,

s

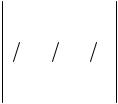
x0 y0 z0

rot F = ∂ ∂x ∂ ∂y ∂ ∂z = ×F.

Fx Fy Fz

Таким образом, ротор – векторная дифференциальная операция над компонентами вектора F, приводящая к получению новой векторной величины rot

F.

Для всякого потенциального поля F = ψ имеем ×F = ×( ψ)≡ 0.

т.е. всегда rotgrad(ψ) = 0. Поэтому потенциальные поля называют также безвих-

ревыми.

Поля, для которых div F = 0, называются соленоидальными. Поскольку всегда ( ×V)≡ 0 , то соленоидальные поля F = rotV.

Если в некоторой области поле не является соленоидальным, причем в каждой точке F ≠ 0 , то все точки области – это источники или стоки.

Потенциальные поля F (для которых ×F = 0 ) могут быть одновременно и соленоидальными F = 0 , тогда они называются гармоническими.

Следующие тождества векторного анализа имеют смысл правил дифференцирования произведения функций.

(ϕψ)= ϕ ψ +ψ ϕ;

(ψF)= ψ F + F ψ;

(F ×V)= V ×F − F ×V;

×(ψF)= ψ ×F + ( ψ×F).

Часто в теории ЭМ используются следующие формулы:

f (ξ)= f ′(ξ) ξ (дифференцирование сложной функции)× ×F = ( F)− 2F (ротор от ротора)

В декартовых координатах:

2F = F = x0∆Fx + y0∆Fy + z0∆Fz - оператор Лапласа. Наиболее важными для теории ЭМ поля являются следующие инте-

гральные соотношения векторного анализа:

Теорема Гаусса – Остроградского

∫ FdV = ∫F ds;

V S

Теорема Стокса

∫( ×F) ds = ∫F dl.

S L

Лекция № 2. Основные объекты электродинамики

Заряды, токи и векторы поля

Классическая теория электромагнетизма является макроскопической. Это значит, что в рассматриваемых процессах проявляется действие огромных

– «практически бесконечных» - количеств элементарных частиц. Структура материи при этом обычно игнорируется. Среда представляется сплошной, а заряды и токи – распределенными в объеме (иногда на поверхности).

Под плотностью заряда ρ понимается величина

где ∆q - заряд, содержащийся в элементарном объеме ∆V. Поскольку заряд дискретен (наименьший по абсолютной величине отрицательный заряд e ≈1.602 10−19 Êë ), то содержащийся в (1) предельный переход следует пони-

мать как условный. Как бы на ни уменьшался объем ∆V, он все же должен содержать достаточно большое число элементарных частиц. Но при переходе к идеализированной сплошной заряженной среде из (1), можно сделать вывод,

что ρ = dqdV .

Плотность тока проводимости j - это вектор

где ∆S - элементарная площадка, ориентированная перпендикулярно движению зарядов, а i0 - орт нормали, указывающий направление движения; ∆I - ток, проходящий через ∆S

В современной физике остается незыблемым закон сохранения зарядов: заряд не уничтожается и не создается из ничего. Если в объеме V, ограниченном поверхностью S, содержится заряд q, который не остается постоянным (т.е. уменьшается или увеличивается), то объяснить это следует тем, что границу пересекают носители заряда. Другими словами, через поверхность S проходит ток, и его величина должна быть связана с зарядом соотношением:

(ток, выходящий через S наружу, считается положительным, а входящий внутрь - отрицательным).

Из (3) получается также дифференциальная формулировка сохранения заряда:

т.к. равенство должно быть справедливым для произвольного объема. Электромагнитное поле описывают при помощи следующих векторных

функций координат и времени

E = E (r, t) - напряженность электрического поля; H = H (r, t) - напряженность магнитного поля; D = D (r, t) - электрическая индукция;

B = B (r, t) - магнитная индукция;

В электромагнитном поле на заряды и токи действуют силы. На точечный заряд, который обычно рассматривают как «пробное» тело для обнаружения и измерения поля, действует сила:

F = q(E +[v,B]),

где q – величина данного заряда, а v- скорость его движения. Под точечным зарядом понимают некоторое заряженное тело, считающееся достаточно малым в условиях эксперимента.

В случае неподвижного заряда (v = 0) сила зависит только от напряженности электрического поля:

F′ = qE.

Это равенство рассматривают в качестве определения E. На движущийся точечный заряд, кроме того, действует сила:

F′′ = q(v ×B),

называемая лоренцовой силой. С появлением этой силы связывают определение вектора магнитной индукции В.

Вектора D и Н в вакууме связаны с Е и В соотношениями:

где ε0 и µ0 - константы, зависящие только от выбора единиц измерения; первая называется электрической постоянной, а вторая – магнитной.

В системе СИ единицы измерения рассмотренных физических величин следующие:

Заряд q [Кл] (Кулон);

Плотность заряда ρ [Кл/м3] (Кулон на кубический метр); Напряженность электрического поля Е [В/м] (Вольт на метр); Напряженность магнитного поля Н [А/м] (Ампер на метр); Электрическая индукция D [Кл/м2] (Кулон на квадратный метр); Магнитная индукция В [Т] (Тесла);

Электрическая постоянная ε0 [Ф/м] (Фарада на метр);

Магнитная постоянная µ0 [Г/м] (Генри на метр).