§2.5. Распределение энергии в спектре периодического сигнала

Положим, что сигнал представляет собой периодическую функцию параметра t с периодом T. Средней за период мощностью сигнала назовем величину

, (2.30)

аналогично тому, как определяется в физике мощность на активном сопротивлении величиной 1 Ом. Представим сигнал в виде ряда Фурье в тригонометрической форме, тогда выражение (2.30) предстанет в виде:

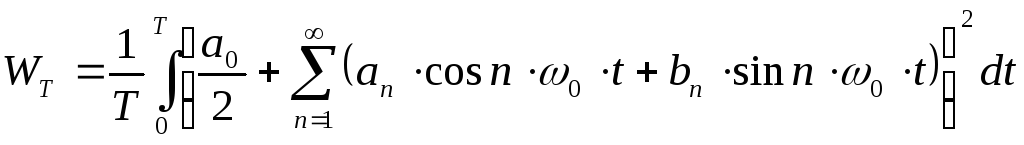. (2.31)

При возведении в квадрат правой части выражения (2.31) появятся слагаемые следующих видов:

1. ;

2. и;

3. произведения синусов и косинусов с аргументами различной кратности.

Постоянная составляющая после интегрирования даст.

Слагаемые второго вида после приведения к форме:

и

и интегрирования в пределах дают

и .

Последний вид слагаемых при интегрировании за период Т обращаются в нуль, как ортогональные функции.

Таким образом, средняя мощность сигнала за период Т выразится следующим соотношением:

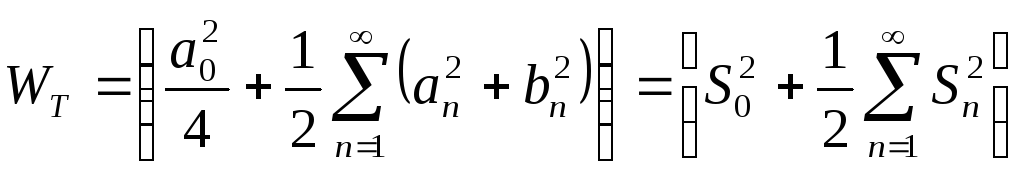, (2.32)

где - постоянная составляющая;

- амплитуда n-й гармоники сигнала.

При использовании ряда Фурье в комплексной форме и с учетом (2.28) получим:

. (2.33)

Итак, средняя мощность сигнала за период T равна сумме средних мощностей постоянной составляющей и гармоник. С энергетической точки зрения отдельные спектральные составляющие сложного периодического сигнала аддитивны, что является результатом ортогональности гармонических функций с кратными частотами.

Важно отметить, что мощность сигнала не зависит от величин фаз отдельных гармоник. Таким образом, изменение формы сигнала из-за изменений фазовых соотношений между отдельными гармониками, входящими в спектр сигнала, не влияет на среднюю мощность сигнала.

По виду функции можно делать выводы о распределенной мощности в спектре периодического сигнала и, следовательно, определять полосу пропускания, обеспечивающую достаточно полное использование мощности сигнала.

§2.6. Преобразование Фурье.

Любой физически реализуемый сигнал является ограниченным по частоте, по времени и обладает конечной энергией. Ограничение по частоте и энергии следует из инерционности и ограничения мощности реально реализуемых источников сигналов и если сигнал обладает конечной энергией, то он должен быть ограничен и во времени.

С математической точки зрения это означает, что функции , отображающие реальные сигналы, удовлетворяют условиям Дирихле и требованию абсолютной сходимости интеграла от модуля функции , то есть

(2.34)

где М - конечная величина.

Очевидно, что непериодический сигнал можно рассматривать как периодический с периодом (Т), стремящимся к бесконечности. Количество гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно возрастать, так как при основная частота

(2.35)

будет стремиться к нулю, а их амплитуды также будут стремиться к нулю.

Следовательно, расстояние между спектральными линиями, равное основной частоте , становится бесконечно малым, а спектр - непрерывным (сплошным).

Таким образом, выражения для спектрального представления непериодического сигнала можно получить предельным переходом (при ) спектра периодического сигнала, выраженного рядом Фурье.

Прямое и обратное преобразование Фурье для периодической функции запишем в форме, аналогичной (2.24):

(2.36)

Периодический сигнал преобразуется в непериодический сигналпутем предельного перехода при. При этом основная частотауменьшается до,превращается в текущую частоту , а операция суммирования заменяется операцией интегрирования. Таким образом, ряд Фурье преобразуется в интеграл Фурье:

. (2.37)

Внутренний интеграл, являющийся функцией ,

(2.38)

называется прямым преобразованием Фурье, а результат этого преобразования называется комплексной спектральной плотностью или спектральной характеристикой функции. Внешний интеграл, являющейся функцией t,

, (2.39)

называется обратным преобразованием Фурье. Эти соотношения безусловно справедливы только для абсолютно интегрируемой функции .Как видно из выражения (2.38), на каждой конкретной частоте значение соответствующей спектральной плотности, а следовательно, и амплитуды равно нулю. Из сравнения выражения (2.39) с рядом Фурье (2.24) видно, что бесконечно малому интервалу частоты соответствует составляющая с бесконечно малой комплексной амплитудой, то есть

. (2.40)

Сравнение выражений (2.38) и (2.25) позволяет пояснить физический смысл понятия «спектральная плотность». Для этого выделив какую-либо дискретную частоту , соответствующую в случае периодической функцииn-й гармонике, найдем амплитуду этой гармоники:

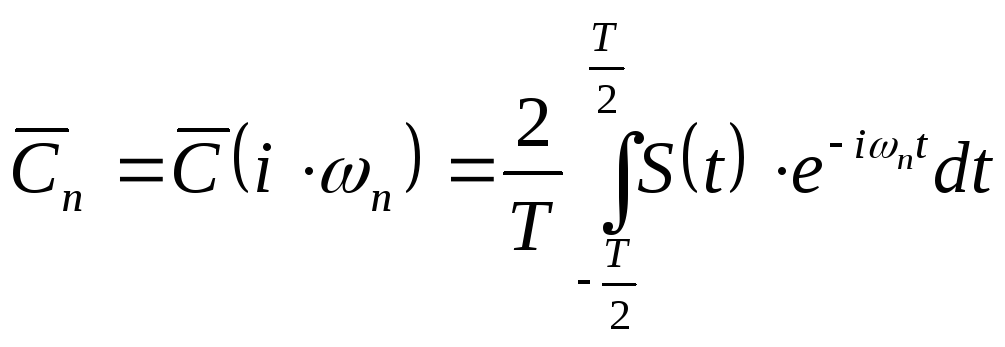. (2.41)

Для непериодической функции, совпадающей с периодической на интервале ее спектральная плотность, соответствующая той же частоте,определяется выражением :

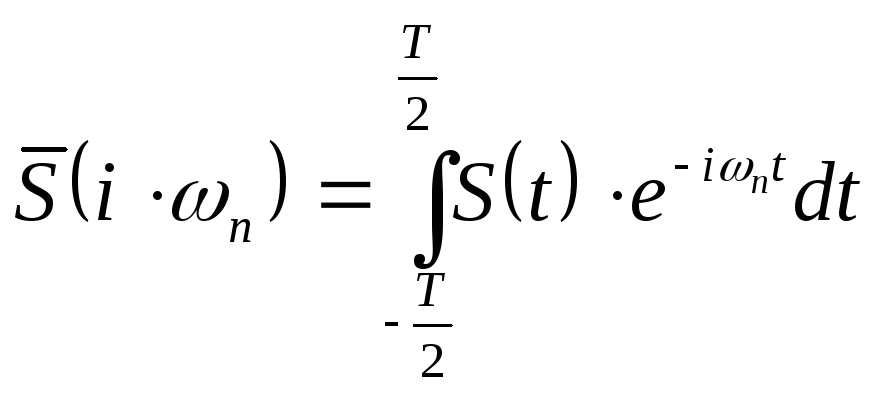, (2.42)

где T - конечно.

Так как интегралы в правых частях выражений (2.41) и (2.42) полностью совпадают, то

. (2.43)

Учитывая, что

,

где - циклическая частота, соответствующая круговой частоте, получим:

. (2.44)

Множитель знаменателя 2 в правой части этого выражения учитывает то, что при использовании экспоненциальной формы ряда Фурье, в которой фигурируют отрицательные частоты, амплитуды гармоник равны половине амплитуд получаемых при одностороннем разложении.

Таким образом, значение спектральной плотности на частоте равно отношению половины амплитуды гармоникик основной частоте периодического сигнала, выраженной в герцах, которая равна полосе частот, отделяющей соседние линии дискретного спектра. Таким образом, физическая суть спектральной плотности – это плотность амплитуд и ее размерность. Из анализа соотношения (2.44) вытекает важное положение: непрерывный спектр (модуль спектральной плотности) непериодической функции и огибающая линейчатого спектра периодической функции совпадают по форме и отличаются только масштабом:

.

Из выражения (2.38) с учетом формулы Эйлера можно получить выражение для спектральной плотности а, следовательно, и прямое преобразование Фурье, в тригонометрической форме:

. (2.45)

Спектральная плотность величина комплексная, поэтому для нее справедливо следующее представление

, (2.46)

где - действительная часть ;

- мнимая часть ;

- модуль или спектр непериодического сигнала;

- фаза .

Так как - четная функция частоты, а- нечетная относительно частоты, то, как и в случае ряда Фурье, модуль спектральной плотности- есть функция четная, а фаза- нечетная относительно частоты.

Обратное преобразование Фурье так же легко привести к тригонометрической форме. Действительно в соответствии с (2.30) и учетом (2.43) имеем:

(2.47)

Второе слагаемое из-за нечетности подинтегрального выражения равно нулю, следовательно:

. (2.48)

Преимуществом тригонометрической формы записи преобразования Фурье является его более простое и удобное физическое толкование.