§2.2. Математические модели представления детерминированных одномерных сигналов
Для удобства в
дальнейшем рассматриваются одномерные
сигналы, зависящие от одного параметра,
например, времени или пространственной
координаты. Предположим также, что
информационные системы являются
инвариантными во времени и линейными.
В связи с тем, что большинство применяемых
моделей информационных систем и каналов
обладают свойствами суперпозиции, то
при прохождении через такие системы
сложного сигнала
его
удобно представить в виде взвешенной
суммы более простых базисных функций
.
, 
,
(2.1)
где
- постоянные коэффициенты;
- интервал
существования сигнала;
- начало
сигнала;
- окончание
сигнала.
Таким
образом, при заданном наборе базисных
функций, сигнал
однозначно определяется совокупностью
безразмерных коэффициентов
,
которая называется дискретным спектром
сигнала, а сами
- спектральными коэффициентами. Избрав
такой вид представления сигнала, следует
помнить, что сигналы конечной длительности
за пределами интервала
,
не равны нулю, а условно считаются
периодически продолжающимися, так как
они представляются выражением (2.1). Если
же необходимо, чтобы ограниченный по
времени сигнал вне интервала
был равен 0, то для его представления
используют выражение:
,
(2.2)
где
- спектральная плотность;
- базисная
функция с непрерывно изменяющимся
параметром ω.
Размерность
обратна
размерности параметра
ω,
а произведение
является аналогом безразмерного
коэффициента
.
С практической
точки зрения базисные функции
следует
выбирать так, чтобы они имели простой
аналитический вид, простую техническую
реализацию, обеспечивали быструю
сходимость ряда (2.1) и позволяли легко
определять коэффициенты
.
Вычисление
спектральных коэффициентов
упрощается, если в качестве совокупности
базовых функций (
)
использовать системы ортогональных
функций.
Систему функций
называют
ортогональной на интервале
,
если для всех
и
,
за исключением
случая
,
справедливо равенство
.
(2.3)
Эта система
ортогональных функций называется
ортонормированной, если для всех
справедливо
выражение
.
(2.4)
Если выражение (2.4) не выполняется и
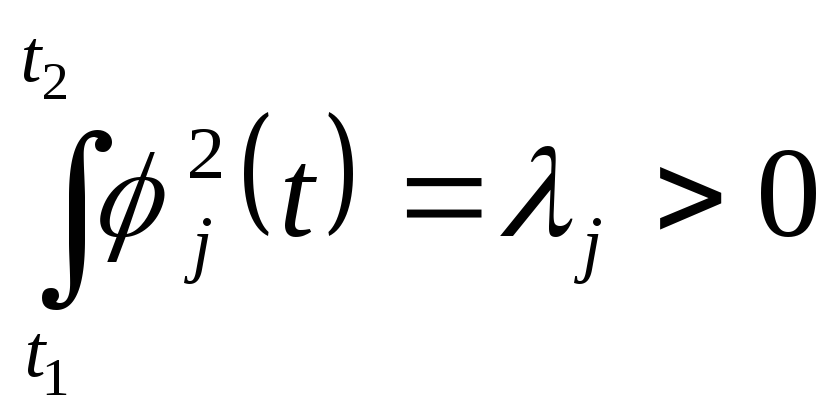, при
,
(2.5)
то систему
ортогональных функций легко отнормировать,
умножив каждую функцию
на свой
коэффициент
.
При использовании
в представлении сигналов в качестве
базисных функций систем ортонормированных
функций, определение спектральных
коэффициентов
не представляет сложности. Действительно,
если сигнал U(t)
представлен совокупностью ортонормированных
функций
в виде:
, 
,
(2.6)
то, полагая, что
интервал
принадлежит интервалу ортогональности,
умножая обе части равенства на
и интегрируя их на интервале
получим
.
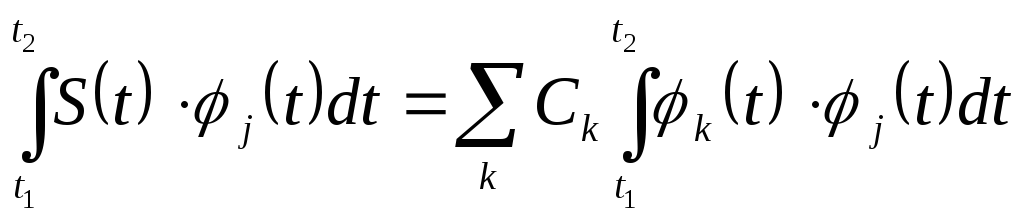(2.7)
В силу
свойства ортогональности все интегралы
в правой части выражения (2.7) при
будут равны
нулю, кроме одного, при
,
который будет равен 1, следовательно
.
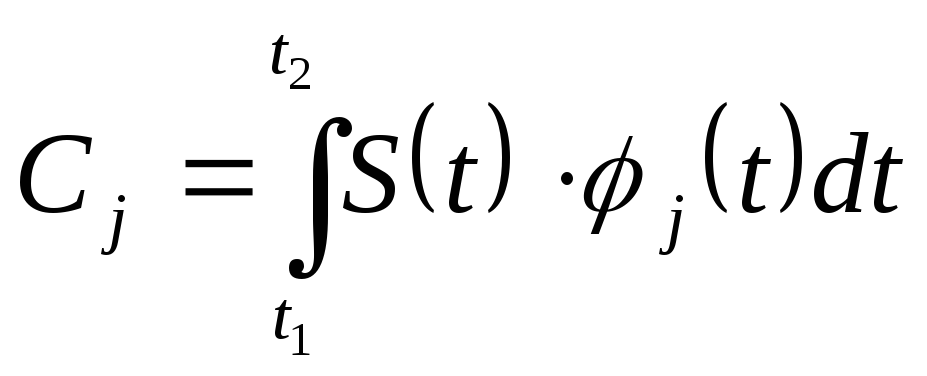(2.8)
Таким образом, могут быть определены все спектральные коэффициенты, входящие в рассмотренную формулу представления сигнала. На практике для представления сигналов наиболее часто используют системы ортогональных функций
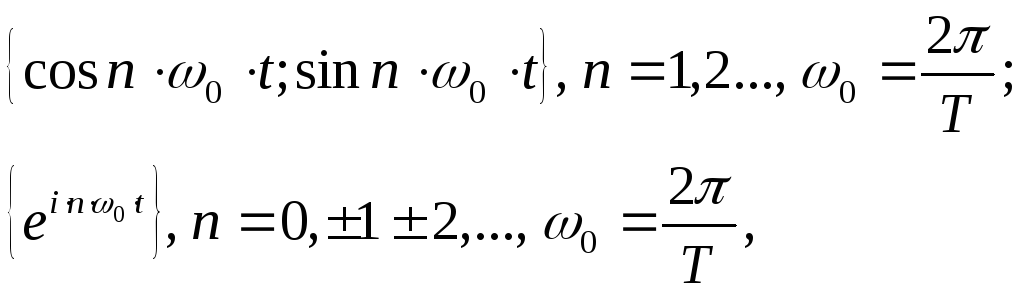(2.9)
где Т - период сигнала.
Для этих целей могут быть использованы системы функций Хаара, системы функций Уолша, ортогональные базисные многочлены Котельникова, Чебышева, Лежандра.
На практике часто используют в качестве системы ортогональных базисных функций совокупность дельта-функций (δ-функция), иногда ее называют функцией Дирака.
Математическое
описание дельта-функции
задается
соотношением:
(2.10)
Такая
математическая модель соответствует
идеальному (абстрактному) импульсу
бесконечно малой длительности и
бесконечно большой амплитуды, имеющего
координату
.
Очевидно,
что спомощью δ-функции
можно выразить значение любого реального
сигнала
при конкретном значении координаты
:
.
(2.11)
Это равенство
справедливо для любого текущего значения
координаты t.
Заменив
наt
и приняв
в качестве переменной интегрирования
ξ,
получим
.
(2.12)
Такая модель
представляет функцию
в виде последовательности примыкающих
друг к другу δ-функций.
Совокупность таких δ-функций
ортогональна, так как они не перекрываются.
Представление сигналов в виде совокупности δ-функций очень полезно при анализе линейных систем, так как установив реакцию системы на единичную δ-функцию (импульсную переходную функцию), можно определить реакцию системы на произвольный входной сигнал, которая соответствует суперпозиции реакций на последовательность смещенных δ-функций с соответствующими весами.