§2.7. Основные свойства преобразования Фурье

1.Свойство линейности.

Если - спектральная плотность сигнала, а- сигнала, то при любых произвольных постоянныхиспектральная плотность сигнала

будет равна

(2.49)

что следует из линейности операции интегрирования.

2.Свойство симметрии.

Если сигнал имеет спектральную плотность , то спектральная плотность сигнала будет.

Действительно, как следует из (2.39) при

. (2.50)

Приведем в этом равенстве последовательно ряд замен переменных:

;

;

.

Следовательно, спектральная плотность сигнала равна 2. Если - четная функция, тои спектральная плотность сигнала равна .

3. Свойство изменения масштаба.

Если сигнал имеет спектральную плотность, то при изменении масштаба исходного сигнала, то есть для сигнала (-любая действительная постоянная) спектральная плотность равна

.

Действительно:

.

Произведем замену переменных , тогда

а) при

; (2.51)

б) при

. (2.52)

Следовательно, спектральная плотность сигнала равна.

4. Свойство частотного сдвига. Если спектральная плотность сигнала, то сигналусоответствует спектральная плотность, то есть умножение сигналанасдвигает весь спектрна частоту.

Для доказательства этого свойства применим обратное преобразование Фурье к спектру и произведем замену переменных, тогда

. (2.53)

Таким образом, сигналу соответствует спектральная плотность.

5. Свойство временного сдвига.

Если есть спектральная плотность сигнала , то сигналу соответствует спектральная плотность. Для доказательства этого свойства применим прямое преобразование Фурье к сигналуи сделаем в нем замену переменных, тогда

. (2.54)

Таким образом, сигналу соответствует спектральная плотность. Другими словами, при сдвиге сигнала на, его амплитудный спектр не меняется, а изменяется только фазовый спектр на величину -.

6. Если сигнал имеет спектральную плотность, а сигнал, то

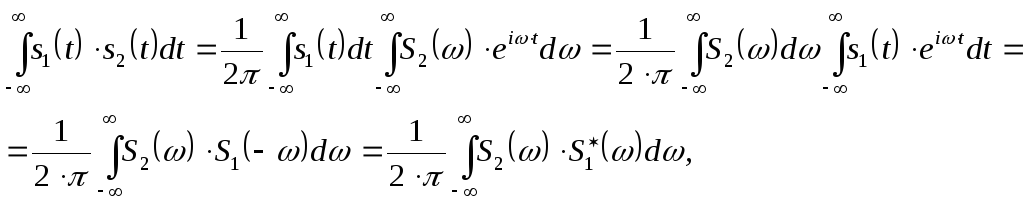(2.55)

где – комплексно сопряженная с функция.

7. Если сигнал со спектральной плотностью проходит через некоторое звено с предаточной функцией , то спектральная плотность выходного сигналаравна

. (2.56)

§2.8. Распределение энергии в спектре непериодического сигнала

Если задан непериодический сигнал , физическим представлением которого может быть электрическое напряжение на активном сопротивлении в 1 Ом, то можно найти количество энергии, выделяемое на этом сопротивлении за время действия сигнала:

. (2.57)

Понятие энергии сигнала имеет смысл только в том случае, если интеграл (2.57) конечен.

Сигналы с конечной энергией называют энергетическими. Если сигналу соответствует спектральная плотность , то используя обратное преобразование Фурье и, меняя порядок интегрирования, можно записать:

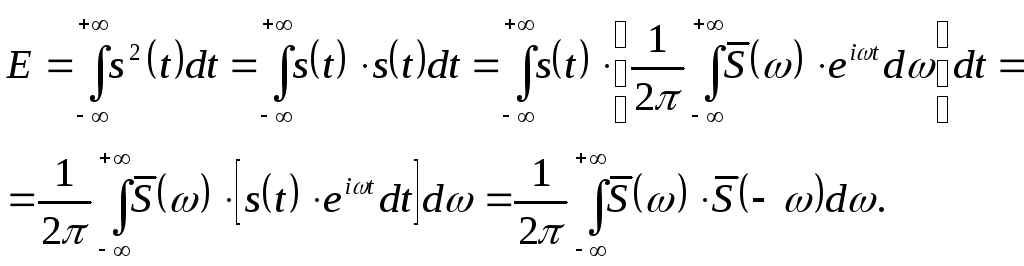(2.58)

Для действительной функции

,

где - комплексно-сопряженна функция, и поэтому

,

причем, как указывалось ранее (§2.4), -четная функция.

Таким образом,

. (2.59)

- называют спектром плотности энергии или спектральной плотностью энергии сигнала, физический смысл которого - энергия, приходящаяся на единицу полосы частот при текущей частоте ω (размерность: ). Соотношение (2.59), известное как равенство Парсеваля, показывает, что энергию, выделяемую непериодическим сигналом за время его действия, можно найти, интегрируя квадрат модуля его спектральной характеристики во всем интервале частот.

В отличие от формулы (2.33) формула (2.59) определяет не среднюю мощность, которая для любого непериодического абсолютно интегрируемого сигнала равна 0 (так как ), а полную энергию, выделяемую сигналом за все время его действия.

Спектральная плотность энергии, характеризующая распределение энергии по спектру сигнала, существует лишь для энергетически ограниченных сигналов (для которых выражение (2.57) конечно), к которым применимо преобразование Фурье. Если же значение интеграла (2.57) бесконечно, то понятие энергии сигнала теряет смысл. В этом случае рассматривают среднюю мощность сигнала. Сигналы с ограниченной мощностью называют мощностными.

Определим среднюю мощность непериодического сигнала как среднюю мощность W, рассеиваемую на активном сопротивлении величиной 1 Ом в течение времени (Т) действия сигнала, тогда:

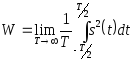. (2.60)

Непериодический сигнал представим конечным по времени сигналом :

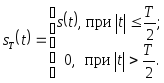(2.61)

При конечном Т сигнал имеет конечную энергию, и тогда, в соответствии (2.59), энергия сигналаопределится из выражения:

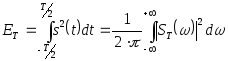, (2.62)

где - спектральная плотность сигнала . Следовательно,

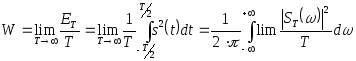. (2.63)

Если предел под знаком интеграла существует, то эта функция называется спектральной плотностью мощности , то есть

. (2.64)

Можно доказать, что и среднюю мощность сигналаW, с учетом четности функции , можно представить в виде:

. (2.65)