§2.9. Корреляционные функции детерминированных сигналов

С физической точки зрения корреляционная функция характеризует взаимосвязь или взаимозависимость двух мгновенных значений одного или двух различных сигналов в моменты времени и. В первом случае корреляционную функцию часто называютавтокорреляционной, а во втором - взаимнокорреляционной. Корреляционные функции детерминированных процессов зависят только от .

Если заданы сигналы и, то корреляционные функции определяют следующимивыражениями:

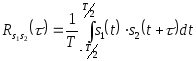- взаимнокорреляционная функция; (2.66)

- автокорреляционная функция. (2.67)

Если и- два периодических сигнала с одинаковым периодом T, то очевидно, что их корреляционная функция тоже является периодической с периодомТ и, следовательно, она может быть разложена в ряд Фурье.

Действительно, если в выражении (2.66) разложим в ряд Фурье сигнал , то получим

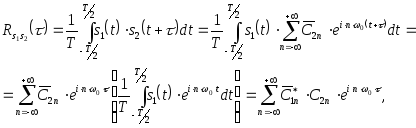(2.68)

где и- комплексные амплитудыn-й гармоники сигналов исоответственно,- комплексно-сопряженный с коэффициент. Коэффициенты разложения взаимнокорреляционной функции можно найти как коэффициенты ряда Фурье

. (2.69)

Частотное разложение автокорреляционной функции легко получить из формул (2.68) и (2.69), положив , тогда

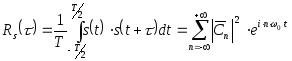. (2.70)

А так как и, следовательно,

, (2.71)

то автокорреляционная функция - четная и поэтому

. (2.72)

Четность автокорреляционной функции позволяет ее разложить в тригонометрический ряд Фурье по косинусам

. (2.73)

В частном случае, при , получим:

.

Таким образом, автокорреляционная функция при представляет собой полную среднюю мощность периодического сигнала , равную сумме средних мощностей всех гармоник.

§2.10. Частотное представление импульсных сигналов

В предыдущем рассмотрении предполагалось, что сигналы непрерывны, однако при автоматической обработке информации часто используются и импульсные сигналы, а также преобразование непрерывных сигналов в импульсные. Это требует рассмотрения вопросов частотного представления импульсных сигналов.

Рассмотрим модель преобразования непрерывного сигнала в импульсную форму, представленную на рис.2.6а.

Пусть на вход импульсного модулятора поступает непрерывный сигнал (рис.2.6б).Импульсный модулятор формирует последовательность единичных импульсов (рис.2.6в) с периодом Т и длительностью импульсов , причем . Математическую модель такойпоследовательности импульсов можно описать в виде функции :

(2.74)

где k - номер импульса в последовательности.

Выходной сигнал импульсного модулятора (рис.2.6г) можно представить в виде:

.

На практике желательно иметь частотное представление последовательности импульсов. Для этого функцию , как периодическую, можно представить в виде ряда Фурье:

, (2.75)

где

- спектральные коэффициенты разложения в ряд Фурье; (2.76)

- частота следования импульсов;

n - номер гармоники.

Подставляя в выражение (2.76) соотношение (2.74), найдем :

, (2.77)

при ;

.

Подставляя (2.76) в (2.74), получим:

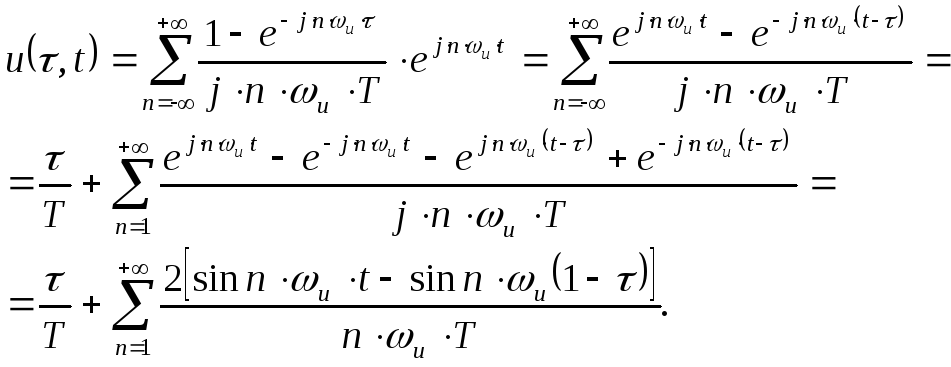(2.78)

Преобразуем разность синусов, тогда

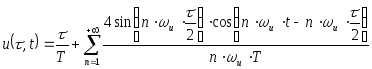. (2.79)

Введем обозначение фазы n-ой гармоники

. (2.80)

Тогда

. (2.81)

Таким образом, последовательность единичных импульсов содержит наряду с постоянной составляющей бесконечное число гармоник с уменьшающейся амплитудой. Амплитуда k-ой гармоники определяется из выражения:

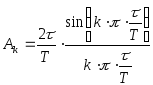. (2.82)

При цифровой обработке сигналов проводится дискретизация (квантование) по времени, то есть преобразование непрерывного сигнала в последовательность коротких импульсов. Как показано выше, любая последовательность импульсов имеет довольно сложный спектр, поэтому возникает естественный вопрос, каким образом процесс дискретизации по времени влияет на частотный спектр исходного непрерывного сигнала.

Для исследования этого вопроса рассмотрим математическую модель процесса дискретизации по времени, представленную на рис.2.7а.

Импульсный модулятор (ИМ) представляется в виде модулятора с несущей в виде идеальной последовательности очень коротких импульсов (последовательности -функций) , период следования которых равенТ (рис.2.7б).

На вход импульсного модулятора поступает непрерывный сигнал (рис.2.7в), а на выходе образуется импульсный сигнал (рис.2.7г).

Тогда модель идеальной последовательности -функций можно описать следующим выражением

, (2.83)

а выходной сигнал , который представляет собой последовательность идеальных импульсов, амплитуды которых соответствуют последовательности мгновенных значений входного сигнала (,,и т.д.) может быть записан в следующем виде:

. (2.84)

Последовательность дискретных значений сигнала , как показано ранее, может бытьпредставлена следующим выражением:

. (2.85)

Так как функция последовательности идеальных импульсов периодическая, то она может быть разложена в ряд Фурье

, (2.86)

где , (2.87)

.

Так как

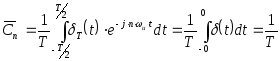, (2.88)

то можно написать

. (2.89)

Таким образом, спектр идеальной последовательности -функции состоит из бесконечного числа гармоник с одинаковой амплитудой . И сигнал на выходе импульсного модулятораможнонайти из соотношения:

. (2.90)