§2.3. Частотная форма представления детерминированных сигналов

Современные системы обработки информации и, в частности, системы обработки изображений являются сложными комплексами взаимодействующих технических устройств, для описания которых часто используют их математические модели. При этом вся система представляется в виде совокупности отдельных инвариантных во времени линейных звеньев, работа каждого из которых описывается либо линейными дифференциальными уравнениями, либо уравнениями в конечных разностях.

При исследовании таких систем решения всегда содержат экспоненциальные функции времени, так как этот класс функций инвариантен по отношению к операциям дифференцирования и интегрирования.

Поэтому для представления детерминированных сигналов широко используются системы базисных функций вида , как при(преобразование Фурье), так и при(преобразование Лапласа). При этих преобразованиях параметром базисных функций является частота (ω).

Причем важно отметить, что использование экспоненциальных базисных функций в преобразовании Фурье попарно (с положительным и отрицательным параметром ω) позволяет, в соответствии с формулами Эйлера, представить сигнал в виде гармонических составляющих, то есть перейти к системе базисных функций вида , которые тоже содержат в качестве параметра частоту (ω).

Поэтому эти методы представления детерминированных сигналов называют частотной формой представления сигнала. Причем первый вид представления (на основе базисных функций вида ) носит название экспоненциального или комплексного, а второй (на основе гармонических базисных функций) - тригонометрического.

Важно отметить, что экспоненциальный и тригонометрический виды представления детерминированного сигнала не являются двумя различными видами представления, а представляют собой лишь различные выражения частотной формы представления сигнала. Анализ работы как отдельных звеньев, так и всей информационной системы в целом, как правило, проводится с помощью частотных методов (основанных на частотном представлении сигнала), теория которых широко разработана и которые позволяют применять широко распространенную измерительную технику. Поэтому представляет большой интерес математическое описание различного вида сигналов и процессов их обработки в частотной области.

§2.4. Математическое описание одномерных сигналов

Одномерные сигналы, как указывалось ранее, представляются функциями одного аргумента, например: . Для представления одномерных сигналов в частной области удобно разделить их на три вида: гармонические, периодические и непериодические.

а) Гармонический сигнал традиционно записывается в следующем виде:

, (2.13)

где - амплитуда гармонического сигнала;

- частота гармонического сигнала;

φ - фаза;

и представляет собой простейший вид одномерных сигналов.

Выражение (2.13) представляет собой тригонометрический вид представления, который может иметь и иную запись, соответствующую разложению по базисным функциям:

, (2.14)

где ,

.

Справедливость этого соотношения легко проиллюстрирует рис.2.1

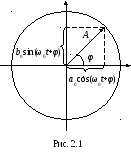
Спектр гармонического сигнала состоит только из одной частоты .

Под спектром сигнала понимается совокупность гармонических сигналов с заданными частотами, амплитудами и фазами, сумма которых даст исходный сигнал.

Наряду с тригонометрической формой представления гармонического сигнала широко используетсся комплексная форма представления. Идея перехода от тригонометрической формы представления к комплексной заключается в следующем. Гармонический сигнал можно представить как проекцию радиуса единичной окружности в комплексной области на действительную ось (рис.2.2). Поэтому имеет место следующее соотношение

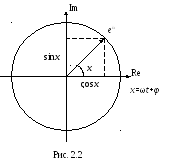. (2.15)

Еще одну форму комплексного представления гармонического сигнала можно получить исходя из формул Эйлера:

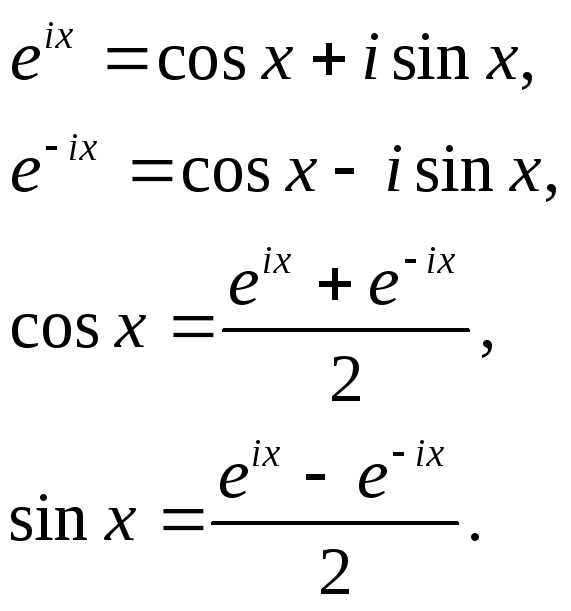
В этом случае получаем следующее соотношение

. (2.16)

Первой из этих форм соответствует векторное представление, изображенное на рис.2.3а.

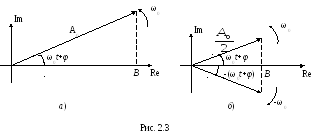
Действительная функция получается в первом случае как проекция OB векторана горизонтальную ось, а во втором –как сумма проекций OB на ту же ось двух векторов с амплитудами, вращающимися с угловой частотойво взаимнопротивоположных направлениях.

В соответствии с этим второе слагаемое в правой части выражения (2.16) можно трактировать как колебание с «отрицательной» частотой, что приводит к следующей записи:

. (2.17)

Нетрудно видеть, что в данном случае «отрицательные» частоты имеют формальный характер и связаны с применением комплексной формы для представления действительной функции времени. Хотя, если рассматривать частоту как скорость изменения фазы гармонического сигнала , то отрицательные частоты приобретают физический смысл и они равноправны с положительным.

Графически амплитудный спектр гармонического сигнала (рис.2.4а), может быть представлен как в виде, показанном на рис.2.4б, так и в виде, показанном на рис.2.4в.

Пусть -периодическая функция, заданная на интервале и удовлетворяющая условию Дирихле (то есть –непрерывна на этом интервале или имеет конечное число точек разрыва первого рода). Таким образом,

,

где -период функции .

В этом случае сигнал может быть представлен в виде ряда Фурье, то есть может рассматриваться как сумма гармонических колебаний с угловыми частотами (представлен в тригонометрической форме):

, , (2.18)

;

причем называется основной частотой, а- соответствующими гармониками или обертонами.

Разложение производится по следующей формуле (тригонометрическая форма):

, (2.19)

где

; (2.20)

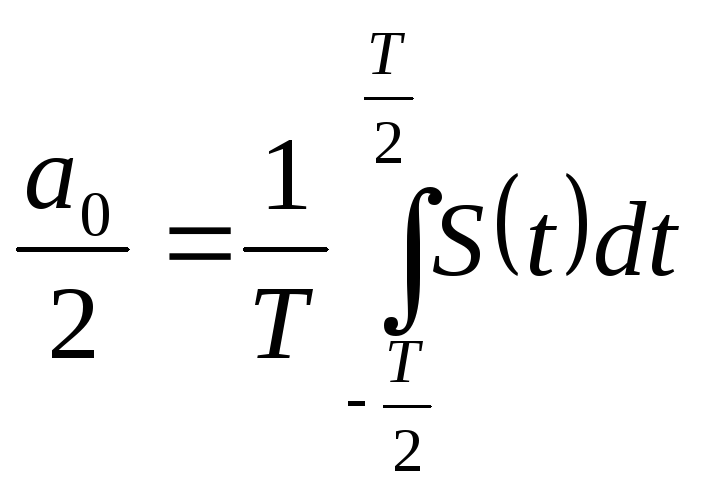- постоянная составляющая; (2.21)

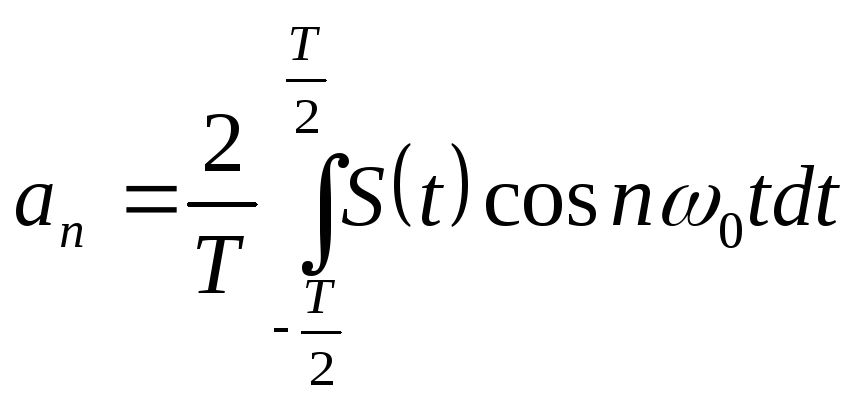; (2.22)

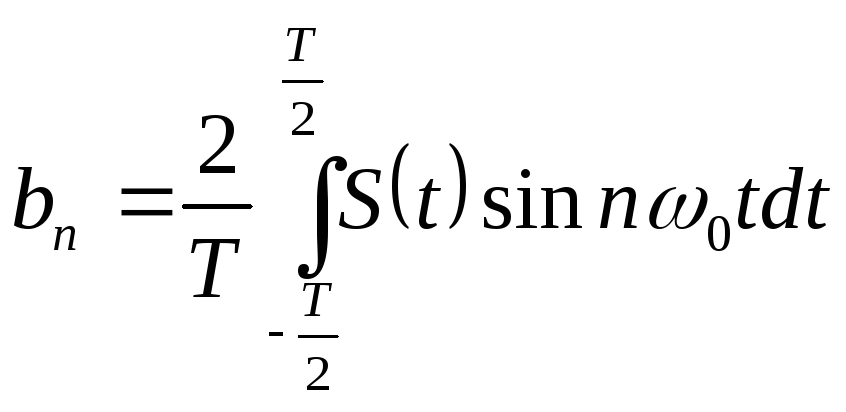. (2.23)

Ряд Фурье может быть записан и в комплексной форме:

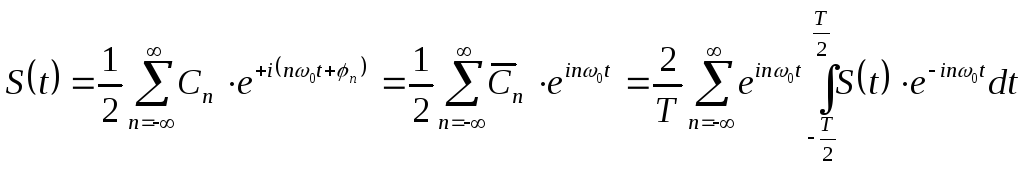, (2.24)

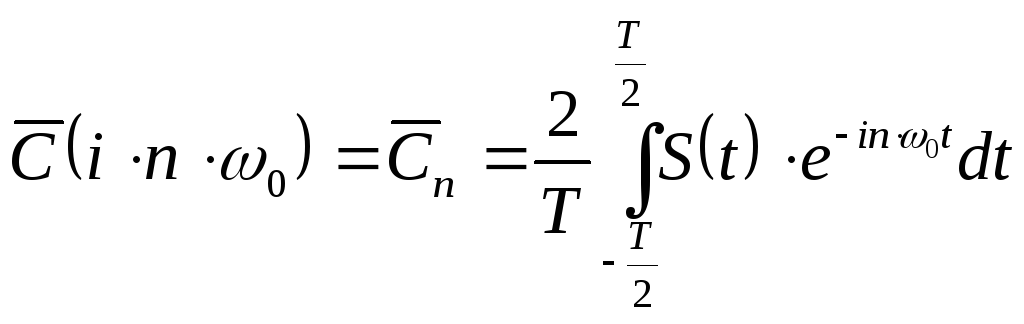, (2.25)

где ; (2.26)

.

Следует еще раз подчеркнуть, что полученные тригонометрический и экспоненциальные разложения в ряд Фурье не являются двумя различными типами рядов, а выражают одно разложение двумя различными способами. Как видно из выше приведенных выражений, коэффициенты одного разложения можно выразить через коэффициенты другого:

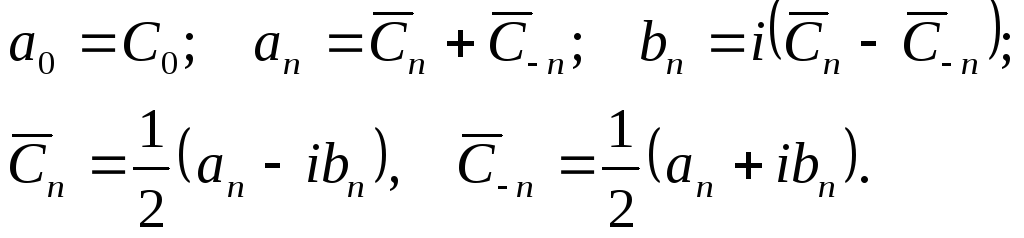(2.27)

Амплитуды и являются взаимосопряженными комплексными величинами и отвечают условию

. (2.28)

При тригонометрическом виде представления функцию называют односторонним (не имеющим отрицательных частот) спектром амплитуд, а функцию - называют спектром фаз (односторонним).

В случае экспоненциального вида представления ряда Фурье функцию принято называть комплексным спектром периодического сигнала, если эту функцию (2.14) представить в виде

; , (2.29)

то функции иназывают соответственно спектром амплитуд и спектром фаз.

Таким образом, если известны спектры амплитуд и спектры фаз сигнала , то в соответствии с (2.19) и (2.24), он может быть однозначно восстановлен.

Как легко заметить из приведенных соотношений, спектры периодических сигналов определены только в дискретных точках , поэтому спектры периодических сигналов называют линейчатыми или дискретными. Такие спектры принято изображать графически в виде вертикальных линий на частотах, причем высота каждой линии пропорциональна амплитуде или фазе соответствующей гармоники, что дает наглядное представление о «ширине спектра» и относительной величине отдельных ее составляющих.

На рис.2.5а показаны примеры амплитуды и фазы одностороннего частотного спектра периодического сигнала, представленного в комплексной форме.

Таким образом, две характеристики: амплитудная и фазовая каждой гармоники определяют частотный спектр периодического сигнала и однозначно его описывают.

Как видно из рис.2.5б двухсторонние спектры периодических сигналов обладают интересной особенностью: спектры амплитуд симметричны относительно оси , а спектры фаз симметричны относительно начала координат. Это легко доказать для общего случая. Действительно, исходя из выражений 2.14, 2.15, 2.16иявляются комплексно-сопряженными величинами, следовательното есть- четная функцияn и график функции - симметричен относительно оси .

Если - действительная величина, то- так же действительная величина и, а если- комплексная величина, то

и .

Следовательно - нечетная функцияn и ее график симметричен относительно начала координат.