§1.4. Цифровая модуляция

Цифровая модуляция широко используется при цифровой обработке сигналов с помощью ЭЦВМ.

Сущность цифровой модуляции заключается в том, что сигнал, соответствующий передаваемому сообщению, подвергается дискретной модуляции по амплитуде и (или) текущему параметру, а полученные отсчеты представляются в виде цифр в какой-либо системе счисления. Цифровые виды модуляции относятся к классам G1-G4 классификации различных видов модуляции (Таблица 1.1).

Цифровые виды модуляции находят широкое применение при передаче и обработке сигналов и сообщений, так как обладают важными достоинствами:

• слабое влияние неидеальности и нестабильности аппаратуры на качество передачи информации;

• высокая помехоустойчивость;

• универсальная форма представления сигналов;

• простое согласование с ЦВМ;

• возможность унификации и стандартизации элементов и устройств обработки и передачи сигналов.

Из недостатков цифровых видов модуляции следует отметить значительное расширение полосы частот, которое требуется для их передачи, и необходимость точной синхронизации сигналов.

Из различного вид цифровых модуляций при обработке сигналов с помощью ЦВМ наиболее широко применяется так называемое аналого-цифровое преобразование, включающее в себя следующие необходимые преобразования непрерывного сигнала:

• дискредитацию (квантование) по уровню;

• дискредитацию (квантование) по времени или по пространственной координате;

• представление полученных отсчетов в какой-либо системе счисления и кодирование.

Очередность выполнения операций дискредитации по уровню и дискредитации по времени не существенна. Однако обе эти операции имеют свои специфические особенности, которые влияют на точность и достоверность аналого-цифрового преобразования, что требует их детального рассмотрения.

§1.5. Дискретизация по уровню (квантование по уровню)

Сущность дискретизации (квантовании) по уровню, как нелинейного преобразования, заключается в том, что все отсчеты непрерывного сигнала , попадающие в интервал дискретизации, представляются одним значением, которое называется квантованным. Таким образом, происходит преобразование непрерывного сигнала в дискретный. Процесс дискретизации по уровню определен, если задана характеристика дискретизации или квантования (рис.1.3), которая связывает интервалы дискретизации и квантованные значения, то есть каждому интервалу дискретизации ставится в соответствие квантованное значение. Часто интервалы квантования выбирают одинаковыми и тогда говорят, что квантование происходит с постоянным шагом.

Характерной особенностью операции квантования по уровню является то, что квантованный сигнал отличается от оригинала даже при полном отсутствии шумов. Действительно, если на вход устройства квантования подается сигнал , а на выходе получаем квантованный сигнал , то они будут отличаться друг от друга на величину  (рис.1.4а).

.

Величину называют шумом квантования, так как искажения, вызываемые квантованием по уровню равносильны искажениям, вызванные источником шума, то есть искажения рассматриваются как шум, вводимый в систему при квантовании. Частота этого шума зависит от частоты квантуемого сигнала и превышает его.

Максимальная амплитуда шума равна шагу квантования, и поэтому для уменьшения шума необходимо уменьшать шаг квантования.

Для определения среднеквадратического значения ошибки квантования по уровню предположим, что непрерывный сигнал имеет равномерную плотность распределения, интервалы дискретизации одинаковы по величине и в качестве квантованных значений выбираются середины соответствующих интервалов дискретизации. В этом случае, при достаточно большом числе интервалов дискретизации, ошибка квантования может быть приближенно представлена в виде графика, состоящего из отрезков прямых линий с различными наклонами (рис.1.4б). Эти отрезки ограничены снизу и сверху половиной шага квантования, исключения составляют шаги, в которых сигнал либо минимален, либо максимален.

Если шаги квантования малы, то среднеквадратическая ошибка приближенно определяется среднеквадратическим значением типичного линейного отрезка.

Для интервалов времени, заключенных между и, то есть

, (1.12)

можно записать уравнение, определяющее типичный линейный отрезок ошибки

, (1.13)

где -наклон отрезка;

t - время отсчитывается от точки пересечения отрезком оси t.

Тогда среднеквадратическая ошибка квантования может быть определена следующим выражением:

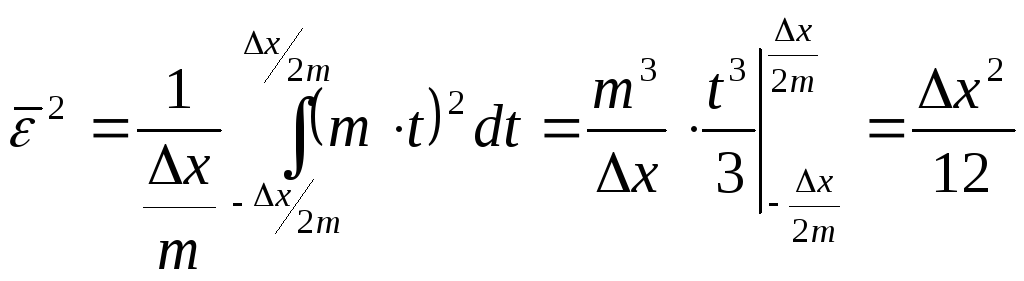. (1.14)

Таким образом, процесс квантования по уровню вносит в сигнал шум квантования, причем среднеквадратическая ошибка квантования по уровню зависит от шага квантования и определяется равенством:

. (1.15)

Следует отметить, что полученное выражение справедливо только в случае выполнения ограничений, указанных выше и которые описывают наиболее типичные условия при выполнении операции дискретизации по уровню.

В случае если плотность распределения сигнала не постоянна или интервалы дискретизации () имеют различную величину или квантованное значениене равно середине интервала дискретизации, выражение для определения среднеквадратической ошибки может иметь иной вид.

Следует также отметить, что, как известно из теории информации, среднее количество информации (I), содержащееся в сообщении x, которую можно выделить из смеси полезного сигнала и шума определяется выражением:

, (1.16)

где – энтропия принятого сообщения;

–энтропия шума.

Таким образом, квантование по уровню снижает среднее количество информации, содержащееся в сообщении.