§1.3. Непрерывные и импульсные модуляции
Если в качестве сигнала-переносчика используются детерминированные непрерывные сигналы, у которых под воздействием передаваемого сообщения информационные параметры изменяются непрерывно, то такие виды модуляции называются непрерывными и по привиденной классификации (Таблица 1.1) они относятся к классу 1.
Наиболее распространенными непрерывными модуляциями являются гармонические модуляции, в которых в качестве переносчика выступает гармоническое колебание
,
(1.4)
где A – амплитуда гармонического колебания;
– частота;
– фаза;
t – время или текущая пространственная координата;
Сигнал-переносчик для такого вида модуляций называют несущим и, как видно из выражения (1.4), он является функцией трех параметров A, , , каждый из которых может быть выбран в качестве информационного.
Если в качестве
информационного параметра используется
амплитуда А,
то говорят об амплитудной модуляции,
при которой модулированный по амплитуде
сигнал
можно описать выражением:
,
(1.5)
где
– модулирующий сигнал, соответствующий
передаваемому сообщению.
Если в качестве
информационного параметра используют
частоту ,
то такой вид гармонической модуляции
называют частотным. При этом виде
модуляции частота несущей является
функцией модулирующего сигнала
и
модулированный по частоте сигнал
может быть
представлен выражением:
.
(1.6)
В качестве
информационного параметра может быть
выбрана фаза сигнала-переносчика ().
В этом случае говорят о фазовой модуляции
и сигнал, модулированный по фазе
представляется в виде:
(1.7)
Применяют и комбинированные виды гармонической модуляции, при которых в соответствии с изменением передаваемого сигнала одновременно меняются два параметра сигнала-переносчика, например, амплитуда и частота. Однако во всех случаях один из параметров не должен изменяться, чтобы играть роль параметра селекции, иначе модулированный сигнал нельзя будет выделить на фоне помех и множества иных подобных сигналов.
Часто в качестве сигнала-переносчика используют детерминированную последовательность импульсов, параметры которой меняются в зависимости от передаваемого сообщения. Такие виды модуляции называют импульсными, и они могут быть отнесены к классам 2, приведенной классификации (Таблица 1.1).
Детерминированная последовательность импульсов может быть описана выражением:
(1.8)
где A – амплитуда импульсов;
T – период следования импульсов;
τ – длительность импульсов;
t – текущее время или текущая пространственная координата;
График детерминированной последовательности импульсов представлен на рис.1.2
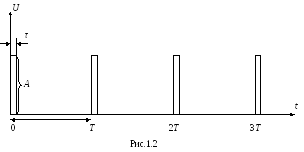
Любой из параметров последовательности импульсов (A, T, τ) может быть использован в качестве информационного.
Если в качестве информационного параметра используют амплитуду А, то такая модуляция называется амплитудно-импульсной, при этом модулированный сигнал можно описать выражением:
(1.9)
где
– модулирующий сигнал, соответствующий
передаваемому сообщению.
Если же в качестве
информационного параметра выбран период
следования импульсов Т,
то такой вид импульсной модуляции
называют частотно-импульсной. При этом
виде модуляции период следования
импульсов (Т)
является функцией модулирующего сигнала
,
и
модулированный сигнал может быть
представлен выражением:
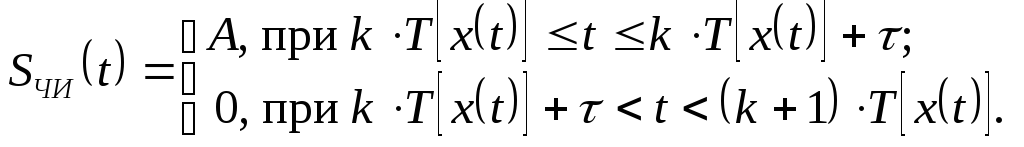(1.10)
В качестве информационного параметра может быть выбрана длительность импульса (). В этом случае говорят о широтно-импульсной модуляции и сигнал, полученный в результате этого вида модуляции может быть представлен в виде:
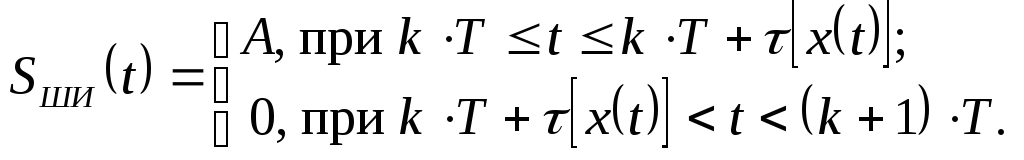(1.11)
Могут использоваться и комбинированные виды импульсной модуляции, при которых в качестве информационных параметров используют сразу два параметра последовательности импульсов, например, амплитуда и частота. В этом случае один сигнал-переносчик может служить для передачи сразу двух сообщений, каждое из которых будет управлять своим информационным параметром.