Преобразование сигналов из временной в частотную область. Описание лабораторной работы выполнено с использованием программного

продукта Mathcad.

Цель работы: Изучение методов получения Фурье-спектров (с помощью стандартных встроенных функций и аналитическим методом) и методов частотной фильтрации.

1. Использование стандартных встроенных функций.

В этом случае преобразование осуществляется над сигналами в виде массива отсчетов сигнала (), число которых (i) равно (m-целое число). Прямое преобразование Фурье для векторавыполняется с помощью стандартной встроенной функции. Результат преобразования представляется в виде векторас количеством комплексных элементов равным. Данное преобразование переводит векториз временной или пространственной области в частотную.

Обратное преобразование осуществляется с помощью стандартной встроенной функции , которая в качестве аргумента использует векторс комплексными

элементами , число которых , а результат представляется в виде вектора с числом элементов.

Задание по п.1. Рассчитать частотный спектр прямоугольного импульса единичной амплитуды, представленного 32 равноотстоящими отсчетами (Т=32) с длительностью импульса равной , где- номер по списку. Представить частотный спектр как в комплексной форме, так и в виде амплитудно-частотной характеристики (АЧХ) и фаза-частотной характеристики (ФЧХ).

С помощью обратного преобразования Фурье восстановить сигнал по его частотному спектру и сравнить с исходным сигналом.

Выполнение п.1:

1. 1. Задать исходный сигнал : i:=0..31 V_i:=if(10+k,1,0)

2. Построить график сигнала V_i.

3. Провести прямое преобразование Фурье сигнала V_i: А:=fft(V)

4. Вычислить АЧХ (М_j) и ФЧХ (Q_j) сигнала (V_i):

j:=0…16

M_j:=

Q_j:=

5. Построить графики АЧХ и ФЧХ.

6. Восстановить сигнал по его частотному спектру V:=ifft(A), нарисовать его график и сравнить его с исходным сигналом.

2. Аналитический метод преобразования сигналов в частотную область.

В этом случае частотный спектр сигнала получают путем разложения его в ряд Фурье по следующим формулам:

,

где

;

;

или

где ; ;

амплитуда и фаза n-ой гармоники соответственно.

Задание по п.2. Разложить в ряд Фурье (20 гармоник) периодический сигнал с периодом Т=1 сек. И длительностью единичного импульса =(0,2+0,01) сек.,где-номер по списку. Построить АЧХи ФЧХ. Синтезировать исходный сигнал по формулам (1) и (2)с использованием с использованием различного числа гармоник (n=3,9,20).

Выполнение п.2.

1. Задать исходный сигнал и построить его график:

Т=1 t=0,0.001…T

.

2. Найти коэффициенты разложения а₀, а_n и b_n по формуле (1) для 20 гармоник.

3. Найти модуль амплитуды () и фазы (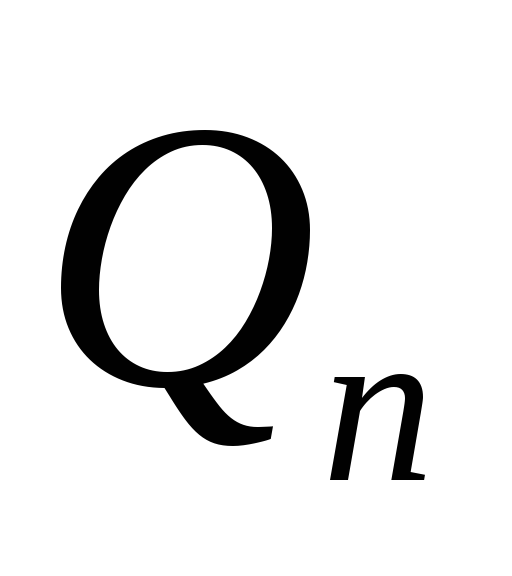) двадцати первых гармоник (n=1…20)и построить АЧХ и ФЧХ.

4. Синтезировать сигнал по формулам (1) и (2) для различного числа гармоник (n=3,9,20), построить соответствующие графики и сравнить их с графиком исходного сигнала.

3. Частотная фильтрация сигналов с целью уменьшения влияния шумов.

Частотная фильтрация шумов основана на том, что шумы, как правило, имеют более высокочастотный спектр, чем полезный сигнал и, кроме того, их мощность, а следовательно и амплитуды их гармоник, значительно меньше по сравнению с амплитудами гармоник полезного сигнала. Исходя из этого частотную фильтрацию можно проводить путем нахождения спектра зашумленного сигнала и исключения из него гармоник с малой амплитудой (частотная фильтрация по уровню) или исключением из него высоко частотных гармоник (высокочастотная фильтрация). В дальнейшем по преобразованному таким образом спектру можно восстановить исходный полезный сигнал.

Задание по п.3. Произвести частотную фильтрацию по уровню и высокочастотную фильтрацию исходного сигнала, заданного своими 128-ю отсчетами вида:

,

зашумленного случайным шумом с максимальной амплитудой равной 1.

Фильтрацию провести при различных уровнях амплитуд исключаемых гармоник (не менее 3) и различных границах исключаемых высокочастотных гармоник (не менее 3). Полученные результаты сравнить с исходным полезным сигналом.

Выполнение п.3.

1. Задать полезный сигнал , аддитивный шуми зашумленный сигнал (),i:=0,1..127 и построить их графики.

2. Найти комплексный частотный спектр с помощью стандартной встроенной функции F:=fft(S), j=0,1..64.

3. Построить график АЧХ сигнала (модулей амплитуд гармоник) .

4. Произвести частотную фильтрацию по уровню исключая из спектра сигнала гармоники с амплитудами менее заданного уровня р (р=0.3,0.5,0.9).

и восстановить сигнал по преобразованному спектру S1:=ifft(g).

5. Построить графики восстановленных сигналов и сравнить их с исходным сигналом.

6. Произвести высокочастотную фильтрацию при различных границах исключаемых высокочастотных гармоник n (n=15,30,50).

и восстановить сигнал по преобразованному спектру: .

7. Построить графики восстановленных сигналов и сравнить их с исходным сигналом.