kotrolnaya_teoreticheskaya_mekhanika_dinamika

Вопросы и задания для самоконтроля

1.Записать формулу для определения модуля силы упругости пружины.

2.Записать дифференциальное уравнение свободных колебаний точки.

3.Записать уравнения свободных колебаний точки.

4.Сформулировать определение понятия «амплитуда сво-

бодных колебаний точки».

5.Сформулировать определение понятия «период свобод-

ных колебаний точки».

6.Сформулировать определение понятия «циклическая частота свободных колебаний точки».

7.Записать дифференциальное уравнение затухающих колебаний точки.

8.Записать уравнения затухающих колебаний точки.

9.Сформулировать определение понятия «период зату-

хающих колебаний точки».

10.Сформулировать определение понятия «амплитуда за-

тухающих колебаний точки».

11.Какие колебания называют колебаниями с малым со-

противлением внешней среды?

12.Записать уравнения апериодического движения точки.

13.Под действием каких сил происходят вынужденные колебания материальной точки?

14.Записать формулу для определения периода возму-

щающей силы.

15.Записать дифференциальное уравнение движения точки под действием восстанавливающей и возмущающей сил.

16.Записать уравнение вынужденных колебаний малой частоты.

17.Записать уравнение вынужденных колебаний большой частоты.

18.Записать условие, при котором происходит явление резо-

нанса.

19.Записать дифференциальное уравнение движения точки, происходящее под действием восстанавливающей силы, возмущающей силы, изменяющейся по периодическому закону, и силы сопротивления движению, пропорциональной первой степени скорости.

71

3.ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ ТОЧКИ

3.1.Дифференциальные уравнения относительного

движения материальной точки. Переносная и кориолисова силы инерции

Два первых закона классической механики и полученные на их основе уравнения справедливы при движении точки в инерциальной системе отсчета (ИСО). Существует ряд технических задач, в которых рассматривают движение материальной точки в подвижной системе отсчета (ПСО), которая в общем случае не является инерциальной.

Инерциальная система отсчета – система отсчета, по отношению к которой изолированная материальная точка находится в покое или движется равномерно и прямолинейно.

Система отсчета, не обладающая этим свойством, называется

неинерциальной системой отсчета

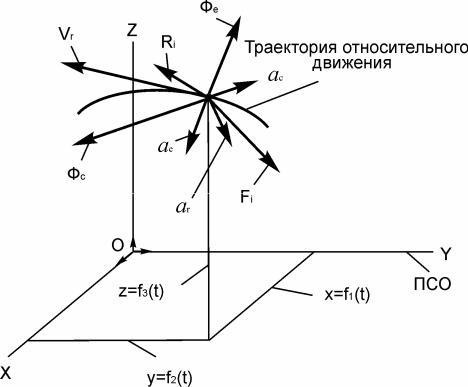
Рассмотрим движение материальной точки под действием активных сил Fi и реакций Ri относительно неинерциальной системы отсчета (рис. 3.1).

Напомним некоторые понятия кинематики, используемые в данном разделе динамики точки.

Движение точки по отношению к неподвижной системе отсчета O1X1Y1Z1 называется абсолютным и характеризуется абсолют-

ной скоростью V и абсолютным ускорением a. Положение точ-

ки на траектории абсолютного движения определяется тремя зависящими от времени координатами, которые называются уравне-

ниями абсолютного движения:

x1 = f1(t); y1 = f2(t); z1 = f3(t).

Неподвижная система отсчета O1X1Y1Z1 является инерциальной. В этой системе отсчета основное уравнение динамики имеет вид

ma = ΣFi + ΣRi,

где Fi – активная сила; Ri – реакция внешней связи.

Движение точки по отношению к подвижной системе отсчета OXYZ называется относительным и характеризуется относи-

тельной скоростью Vr и относительным ускорением ar. По-

ложение точки на траектории относительного движения определяется тремя зависящими от времени координатами, которые назы-

ваются уравнениями относительного движения:

72

х = f4(t); y = f5(t); z = f6(t).

Рис. 3.1

Подвижная система отсчета OXYZ не является инерциальной. Применение в чистом виде первого и второго законов классической механики в ИСО неправомерно.

Рассмотрим переносное движение точки (рис. 3.2) и напомним суть некоторых понятий кинематики, используемых в этом разделе динамики.

Если координаты точки в ПСО постоянны (x = C1 = const; y = C2 = const; z = C3 = const), то движение этой точки вместе с ПСО по отношению к неподвижной системе отсчета называют переносным движением. Это движение характеризуется переносной ско-

ростью Ve и переносным ускорением ae. Положение точки на траектории переносного движения определяется тремя зависящими от времени координатами, которые называют уравнениями пере-

носного движения:

Из курса кинематики известно, что абсолютное ускорение a точки определяют по формуле

73

a = ar + ae + ac,

где ar – относительное ускорение; ae – переносное ускорение; ac – ускорение Кориолиса.

Рис. 3.2

Ускорение Кориолиса определяют по формуле

ac = 2(ωе × Vr),

где ωе – вектор угловой скорости переносного вращения.

Модуль кориолисова ускорения находят по формуле

ac = 2ωe·Vr·sin(ωе,Vr).

Кориолисово ускорение равно нулю в трех случаях:

1)если ωe = 0, т. е. в случае поступательного переносного движения или в момент обращения в нуль угловой скорости непоступательного переносного движения;

2)если Vr = 0, т. е. в случае относительного покоя точки или в момент равенства нулю относительной скорости движущейся точки;

3)если sin(ωе,Vr) = 0, т. е. в случае, когда вектор относительной скорости Vr и вектор переносной угловой скорости ωе

параллельны.

Направление кориолисова ускорения определяется по правилу векторного произведения. Согласно этому правилу вектор ac одно-

74

временно перпендикулярен векторам ωе и Vr. При этом ac направлено в сторону, откуда поворот вектора ωе к вектору Vr для совмещения их направлений виден происходящим против хода часовой стрелки. Поворот осуществляется на угол меньше 180о.

Для определения направления ускорения Кориолиса исполь-

зуют также правило Жуковского: для определения направления ускорения Кориолиса необходимо относительную скорость Vr точки спроецировать на плоскость, перпендикулярную оси вращения, и повернуть эту проекцию в той же плоскости на угол 90о в сторону переносного вращения.

Если подставим абсолютное ускорение a = ar + ae + ac в основное уравнение динамики точки ma = ΣFi + ΣRi, то получим

m(ar + ae + ac) = ΣFi + ΣRi.

Разрешим это уравнение относительно mar: mar = ΣFi + ΣRi – mae – mac.

Введем два вектора: Фе = – mae; Фс = – mac. Эти векторы назо-

вем переносной и кориолисовой силами инерции.

При исследовании движения механических систем в теоретической механике используют следующие понятия.

Сила инерции – величина, равная произведению массы материальной точки на ее ускорение и направленная противоположно этому ускорению.

Переносная сила инерции при рассмотрении движения материальной точки в неинерциальной системе отсчета – величина, равная произведению массы точки на ее переносное ускорение и направленная противоположно этому ускорению.

Кориолисова сила инерции при рассмотрении движения точки в неинерциальной системе отсчета – величина, равная произведению массы точки на ее кориолисово ускорение и направленная противоположно этому ускорению.

Используя понятия переносной и кориолисовой сил инерции, получим

mar = ΣFi + ΣRi + Фе + Фс.

Последнее выражение называют дифференциальным уравнением относительного движения точки в векторной форме или ос-

новным уравнением динамики относительного движения.

75

Произведение массы m точки на ее относительное ускорение ar равно геометрической сумме активных сил Fi, реакций внешних связей Ri, переносной силы инерции Фе и кориолисовой силы инерции Фс.

Проецируя последнее векторное равенство на координатные оси ПСО, получим дифференциальные уравнения относительного движения точки:

mx = ΣFiоx + ΣRiоx + Феоx + Фсоx; my = ΣFiоy + ΣRiоy + Феоy + Фсоy;

mz = ΣFiоz + ΣRiоz + Феоz + Фсоz.

Произведение массы точки на проекцию ее относительного ускорения на координатную ось ПСО равно сумме проекций активных сил, реакций внешних связей и переносной и кориолисовой сил инерции на ту же ось.

Силы инерции Фе, Фс направлены противоположно ускорениям ae, ac (рис. 3.3).

Рис. 3.3

Дифференциальные уравнения относительного движения точ-

ки (mx = ΣFiоx + ΣRiоx + Феоx + Фсоx; my = ΣFiоy + ΣRiоy + Феоy + Фсоy; mz = ΣFiоz + ΣRiоz + Феоz + Фсоz) отличаются от дифференциальных

76

правой части этих уравнений проекций на соответствующие координатные оси переносной и кориолисовой сил инерции.

3.2. Частные случаи относительного движения материальной точки

Случай 1.

Переносное движение – неравномерное вращение тела вокруг неподвижной оси, относительное движение – прямолинейное (рис. 3.4).

Рис. 3.4

В этом случае переносное ускорение ae равно геометрической сумме центростремительного и вращательного ускорений:

ae = aeω +aeε ,

где aeω, aeε – соответственно центростремительное и враща-

тельное переносные ускорения.

В соответствии с этим имеем

77

Фе = – mae = – m(aeω +aeε ) = – maeω – maeε = Фωе + Фεе ,

где Фωе = – maeω – центробежная переносная сила инерции;

Фεе = – maeε – вращательная переносная сила инерции.

Для рассматриваемого случая модули переносных центробежной и вращательной сил инерции находят по формулам:

Фωе = m(ωe)2x; Фεе = mεx.

Основное уравнение динамики и дифференциальные уравнения относительного движения точки в этом случае описываются следующими выражениями:

mar = ΣFi + ΣRi + Фωе + Фεе + Фс; mx = ΣFiоx + ΣRiоx + Фωеох + Фεеох + Фсоx; my = ΣFiоy + ΣRiоy + Фωеоу + Фεеоу + Фсоy; mz = ΣFiоz + ΣRiоz + Фωeoz + Фεeoz + Фсоz.

Случай 2.

Переносное движение – равномерное вращение (ωe = const) вокруг неподвижной оси, относительное движение – прямолинейное

(рис. 3.5).

Рис. 3.5

78

В этом случае угловое ускорение переносного вращения εе = 0 и, следовательно, переносная вращательная сила инерции Фе = 0. Тогда основное уравнение динамики и дифференциальные уравнения относительного движения точки описываются выражениями:

mar = ΣFi + ΣRi + Фωе + Фс; mx = ΣFiоx + ΣRiоx + Фωеох + Фсоx; my = ΣFiоy + ΣRiоy + Фωеоу + Фсоy; mz = ΣFiоz + ΣRiоz + Фωeoz + Фсоz.

Случай 3.

Переносное движение – поступательное неравномерное криволинейное движение, относительное движение – прямолинейное

(рис. 3.6).

Рис. 3.6

Согласно рис. 3.6 механизм содержит кривошипы 1, 2 и прямоугольную пластину 3, по которой перемещается материальная точка по закону x = f(t). Кривошипы 1, 2 совершают вращательные движения, а пластина 3 – поступательное движение.

79

В рассматриваемом случае имеем ωе = 0 и Фс = 0, поэтому основное уравнение динамики относительного движения принимает вид

mar = ΣFi + ΣRi + Фе,

где Фе = – mae – переносная сила инерции.

Так как переносное движение является поступательным, то его ускорение ae равно ускорению точки А тела D. С другой стороны, точка А принадлежит кривошипу О1А, совершающему вращательное неравномерное движение (ωе ≠ 0; εе ≠ 0). Тогда

ae = aА = aAω +aAε = aen +aeτ ,

где aAω, aAε – соответственно центростремительное и вращательное ускорения точки А кривошипа О1А; aen, aeτ – соответственно нормальное и касательное переносные ускорения.

Отсюда вытекает очевидные равенства:

aen =aAω = ω2·r; aeτ = aAε = ε·r; Фen = – maen ; Феτ = – maeτ ,

где Фen , Феτ – переносные нормальная и касательная силы инерции.

С учетом того, что Фе = Фen +Феτ , имеем:

mar = ΣFi + ΣRi + Фen + Феτ ; mx = ΣFiоx + ΣRiоx + Фneox + Фeox ; my = ΣFiоy + ΣRiоy + Фneoy + Фeoy ; mz = ΣFiоz + ΣRiоz + Фneoz + Фeoz .

Случай 4.

Переносное движение – поступательное прямолинейное и равномерное. В этом случае имеем: ωе = 0; ae = 0 и, следовательно, Фс = 0, Фе = 0. Тогда основное уравнение динамики относительного движения принимает вид

mar = ΣFi + ΣRi.

Это уравнение не отличается от основного уравнения динамики материальной точки в инерциальной системе отсчета, которое имеет вид

ma = ΣFi + ΣRi.

80