kotrolnaya_teoreticheskaya_mekhanika_dinamika

4. ГЕОМЕТРИЯ МАСС МЕХАНИЧЕСКОЙ СИСТЕМЫ

4.1. Центр масс механической системы

Напомним некоторые понятия, которые широко применяются в этом учебно-методическом пособии.

Механической системой называют такую совокупность материальных точек, в которой положение или движение каждой точки зависит от положения и движения всех остальных.

Механическую систему, движение которой не ограничено связями, а определяется только действующими на нее силами, назы-

вают свободной механической системой.

Механическая система, движение которой ограничивается наложенными на ее точки внешними связями, называется несвобод-

ной механической системой.

Все силы, действующие на точки механической системы, делят на внешние и внутренние силы.

Внешними называют силы, действующие на точки данной механической системы со стороны материальных тел, не входящих в данную механическую систему.

К внешним силам относятся активные (задаваемые) силы и реакции внешних связей. Активные силы условимся обозначать

FiE , реакции внешних связей – REi .

Внутренними силами называют силы взаимодействия между точками данной механической системы. Внутренние силы условим-

ся обозначать RiJ .

Неизменяемая механическая система – механическая сис-

тема, в которой материальные точки имеют постоянные массы, а связи между точками не деформируются.

Следует отметить, что в данном учебно-методическом пособии рассматриваются только неизменяемые механические системы.

Движение точек механической системы зависит от активных сил FiE , реакций внешних связей REi и внутренних сил RiJ .

Рассмотрим движение несвободной механической системы в инерциальной системе отсчета OXYZ (рис. 4.1).

На рис. 4.1 использованы следующие обозначения: Vi, ai – скорость и ускорение центра сi тяжести i-й точки механической системы; FiE , REi , RiJ – соответственно активная сила, реакция внешней

связи, внутренняя сила, приложенные к i-й точке механической системы; xci, yci, zci – координаты конца радиус-вектора rci центра тяже-

101

сти i-й точки механической системы; Vс, aс – скорость, ускорение центра масс механической системы; FE= ΣFiE , RE = ΣREi , RJ = ΣRiJ – соответственно главные векторы активных сил, реакций внешних связей, внутренних сил; xc, yc, zc – координаты конца радиус-вектора

Рис. 4.1

rc центра масс механической системы.

Необходимо отметить, что для неизменяемых механических систем главный вектор внутренних сил RJ = ΣRiJ всегда равен нулю

(RJ = 0).

Каждая i-я точка механической системы имеет определенную массу mi , а ее положение в системе отсчета OXYZ в любой момент времени определяется радиус-вектором rci или тремя координатами:

xci, yci, zci.

За центр масс механической системы принимают геомет-

рическую точку С, радиус-вектор которой равен rc = Σmirci/m,

где m – масса механической системы.

Центр масс механической системы – геометрическая точка, для которой сумма произведений масс всех матери-

102

альных точек, образующих механическую систему, на их ра- диус-векторы, проведенные из этой точки, равна нулю.

Проецируя последнее векторное равенство на координатные оси системы отсчета OXYZ, получим формулы, определяющие ко-

ординаты центра масс механической системы: xc = Σmixci/m; yc = Σmiyci/m; zc = Σmizci/m.

Эти формулы называют уравнениями движения центра масс механической системы.

Как видно из последних формул, положение центра масс механической системы в любой момент времени зависит только от положения и массы каждой точки этой системы.

Центр тяжести системы тел совпадает с их центром масс. По-

нятие «центр масс механической системы» более широкое по сравнению с понятием «центр тяжести», так как последнее понятие применяется только для твердого тела или системы твердых тел, находящихся в однородном поле сил тяжести.

Дифференцируя по времени векторное равенство rc=Σmirci/m, несложно определить векторы скорости Vc и ускорения aс центра масс механической системы, их проекции на координатные оси, модули и направляющие косинусы:

Vc = drc/dt = ΣmiVci/m; aс = d2rc/dt2 = Σmiaci/m; xc = Σmixci/m;

yc = Σmiyci/m; zc = Σmizci/m;

хс = Σmiхсi/m; yс = Σmiyсi/m; zс = Σmizсi/m;xс = Σmixci /m;yс = Σmiyci /m;zс = Σmizci/m;

Vc = (xc )2 +(yc )2 +(zc )2 ; aс = (xc )2 +(yc )2 +(zc )2 ;

cos(Vc, i) = хс / Vc; cos(Vc, j) = yс / Vc; cos(Vc, k) = zс / Vc; cos(aс, i) = xс /aс;

103

cos(aс, j) = yс /aс; cos(aс, k) = zс /aс.

4.2. Алгоритм определения кинематических характеристик центра масс механической системы

Решение задач, в которых требуется определить уравнение траектории движения центра масс, его скорость и ускорение, проводят по алгоритму, представляющему собой заданную последова-

мы по формулам: xc = Σmixci/m; yc = Σmiyci/m; zc = Σmizci/m. По-

лученные координаты xc, yc, zc окажутся функциями времени, т. е. эти координаты окажутся параметрическими уравнениями движения центра масс.

5.Для нахождения явных уравнений траектории движения центра масс системы материальных точек надо из последних уравнений исключить время t.

6.Определить проекции хс , yс , zс скорости центра масс и

7. Для ориентации вектора скорости Vc центра масс в пространстве определить направляющие косинусы по формулам:

рактеристики центра масс. Результаты вычислений свести в таблицу и при необходимости проиллюстрировать рисунком.

104

4.3. Моменты инерции твердого тела. Радиус инерции

При поступательном движении твердого тела, так же как и при движении материальной точки, мерой инертности является масса. При вращательном движении твердого тела мерой его инертно-

сти является момент инерции относительно оси вращения.

Напомним, что в теоретической механике твердое тело рассматривается как механическая система, образованная непрерывной совокупностью взаимосвязанных материальных точек.

Момент инерции механической системы относительно оси – величина, равная сумме произведений масс всех материальных точек, образующих механическую систему, на квадраты их расстояний от данной оси.

Рассмотрим твердое тело как множество материальных точек Mi с координатами xi, yi, zi (рис. 4.2).

Рис. 4.2

Согласно определению моменты инерции Jox, Joy, Joz относительно соответствующих координатных осей OX, OY, OZ вычисляют

по формулам:

Jox = Σmi((yi)2+(zi)2); Joy = Σmi((xi)2 + (zi)2); Joz = Σmi((xi)2+(yi)2).

105

Момент инерции относительно оси характеризует распре-

деление масс материальных точек относительно этой оси.

Момент инерции всегда положителен и имеет размерность кг/м2.

Момент инерции твердого тела относительно оси, проходящей через его центр масс, всегда имеет минимальное значение.

Формулы для определения моментов инерции некоторых однородных твердых тел приведены в табл. 4.1.

При выполнении курсовых заданий довольно часто требуется определить момент инерции относительно оси, которая через центр

106

масс тела не проходит. Для этой цели используют теорему Штейнера о зависимости между моментом инерции твердого тела относительно параллельных осей.

Момент инерции твердого тела относительно оси ра-

вен сумме его момента относительно параллельной оси, проходящей через центр масс С, и произведения массы твердого тела на квадрат расстояния между параллельными осями.

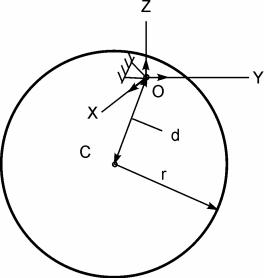
Согласно этой теореме определим момент инерции круглой однородной пластины относительно оси ОХ (рис. 4.3).

Рис. 4.3

Jox = Jcx +m(ОС)2 = Jcx + md2 = mR2/2 + md2.

Для твердого тела в случае неоднородного распределения масс в его поперечном сечении, перпендикулярном оси вращения,

момент инерции вычисляют по формуле

Jox = m(iох)2,

где iох – радиус инерции тела относительно оси вращения ОХ, м.

Радиус инерции твердого тела относительно оси вра-

щения – величина, произведение квадрата которой на массу тела равно моменту инерции тела относительно этой оси.

Таким образом, если поперечное сечение твердого тела по отношению к оси его вращения имеет сложную конфигурацию, то массу тела располагают равномерно на окружности, радиус которой равен радиусу инерции i.

107

Радиус инерции определяют экспериментальным путем по специальной методике.

Если надо вычислить момент инерции механической сис-

темы, состоящей из нескольких твердых тел, причем момент инерции каждого из порознь взятых твердых тел известен, то момент инерции системы определяют как сумму моментов инерции всех твердых тел, входящих в систему, относительно той же оси.

Jox = ΣJiox,

где Jiox – момент инерции i-го тела механической системы относительно оси вращения ОХ.

Для механических систем в теоретической механике исполь-

зуют понятие «радиус инерции механической системы относительно оси вращения».

Радиус инерции механической системы относительно оси вращения – величина, квадрат которой равен отношению момента инерции механической системы относительно данной оси к массе этой системы.

iox = Jox /m.

Вопросы и задания для самоконтроля

1.Сформулировать определение понятия «механическая система».

2.Сформулировать определение понятия «свободная меха-

ническая система».

3.Сформулировать определение понятия «несвободная ме-

ханическая система».

4.Сформулировать определение понятия «внешние силы».

5.Сформулировать определение понятия «внутренние си-

лы».

6.Сформулировать определение понятия «неизменяемая механическая система».

7.Сформулировать определение понятия «центр масс ме-

ханической системы».

8.Записать формулу для определения радиус-вектора цен-

тра масс механической системы.

9.Записать формулу для определения главного вектора активных сил.

10.Записать формулу для определения главного вектора реакций внешних связей.

11.Записать формулу для определения главного вектора реакций внутренних связей.

108

12.Записать формулу для определения вектора скорости центра масс механической системы.

13.Записать формулу для определения вектора ускорения центра масс механической системы.

14.Записать формулы для определения проекций вектора

скорости центра масс механической системы на координатные оси.

15.Записать формулы для определения проекций вектора

ускорения центра масс механической системы на координатные оси.

16.Записать формулу для определения модуля скорости центра масс механической системы.

17.Записать формулу для определения модуля ускорения центра масс механической системы.

18.Что является мерой инертности при поступательном движении твердого тела?

19.Что является мерой инертности при вращательном движении твердого тела?

20.Сформулировать определение понятия «момент инер-

ции тела относительно оси вращения».

21.Что характеризует момент инерции тела относительно оси вращения?

22.Сформулировать теорему Штейнера.

23.Записать формулу для определения момента инерции тела относительно вертикальной оси вращения.

24.Сформулировать определение «радиус инерции твер-

дого тела относительно оси вращения».

25.Записать формулу для определения момента инерции механической системы.

109

5.ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

5.1.Теорема о движении центра масс механической системы

Рассмотрим движение неизменяемой механической системы, находящейся под действием активных сил FiE , реакций REi внешних связей и внутренних сил RiJ в инерциальной системе отсчета OXYZ (рис. 5.1).

Рис. 5.1

Поскольку главный вектор внутренних сил RJ = ΣRiJ = 0, то

теорема о движении центра масс неизменяемой механической системы выражается векторным равенством:

mac = ΣFiE + ΣREi = FE + RE,

где FE = ΣFiE – главный вектор активных сил; RE = ΣREi – главный вектор реакций внешних связей.

Произведение массы механической системы на ускорение ее центра масс равно геометрической сумме приложенных к ней активных сил и реакций внешних связей.

110