Задачи для самостоятельного решения

Задача 1. Найти методом моментов оценку параметра рас­пределения Пуассона.

Задача 2. Найти методом моментов оценку параметра р (веро­ятности «успеха») для геометрического распределения.

Задача 3. Найти методом моментов оценку параметра для геометрического распределения с вероятностью «успеха» ,.

Задача 4. В случае сдвинутого показательного распреде-ления с помощью метода моментов найти оценки и параметров исоответственно.

Задача 5. Найти методом моментов оценку параметра гам­ма-распределения

Задача 6. Пусть случайная величина Х равномерно распреде­лена на отрезке [а, b]. Найти методом моментов оценки для а и b.

Задача 7. Пусть случайная величина Х равномерно распре­делена на []. Найти методом моментов оценки дляc и d.

Задача 8. Найти оценку методом моментов для параметра распределения Лапласа, заданного функцией плотности.

Задача 9. Случайная величина Х (число семян сорняков в пробе зерна) распределена по закону Пуассона .

Ниже приведено распределение семян сорняков в n = 1000 пробах зерна (в первой строке указано количество сорняков в одной пробе; во второй строке указана частота – число проб, содержащих семян сорняков):

	0	1	2	3	4	5	6
	405	366	175	40	8	4	2

Найти методом моментов точечную оценку параметра . Оце­нить вероятность того, что в пробе зерна не будет сорняков.

Задача 10. Случайная величина Х (срок службы изделия) име­ет показательное распределение . В таблице при­ведены сгруппированные данные по срокам службы (в часах) дляn = 200 изделий.

	2,5	7,5	12,5	17,5	22,5	27,5
	133	45	15	4	2	1

Найти методом моментов точечную оценку неизвестного па­раметра показательного распределения. Оценить время, кото­рое изделие прослужит с вероятностью 90 %.

Задача 11. Случайная величина Х (уровень воды в реке по срав­нению с номиналом) подчинена гамма-распределению, плотность которого определяется параметрами и: . В таблице приведены сгруппированные данные по уровням воды (в см) для паводков.

	37,5	62,5	87,5	112,5	137,5	162,5	187,5	250	350
	1	3	6	7	7	5	4	8	4

Найти методом моментов точечные оценки неизвестных па­раметров ирассматриваемого гамма-распределения.

Задача 12. Проведено исследование посещаемости популяр-но­го интернет-сайта. В течение многих часов регистрируется число посетителей, посетивших сайт в течение данного часа. Результа­ты исследования представлены в таблице.

Число посетителей	Количество часов	Число посетителей	Количество часов
0	57	7	139
1	203	8	45
2	383	9	27
3	525	10	10
4	532	11	4
5	408	12	1
6	273	14	1

В предположении, что случайное число посетителей описы­вается распределением Пуассона, оценить параметр методом моментов. Оценить вероятность того, что в течение часа на сайте не будет ни одного посетителя.

Задача 13. Проведено исследование посещаемости популяр­ного интернет-сайта. В течение многих часов регистрируется число посетителей, посетивших сайт в течение данного часа. Результаты исследования представлены в таблице.

Число посетителей	Количество часов	Число посетителей	Количество часов
0	12	7	103
1	108	8	24
2	316	9	13
3	551	10	2
4	632	11	0
5	492	12	0
6	273	14	0

В предположении, что случайное число посетителей опи­сывается биномиальным распределением с числом испытаний , оценить параметр р методом моментов. Оценить вероятность того, что в течение часа на сайте будет не более одного по­сетителя.

Задача 14. В поселке Червонцево все жители имеют доход не менее 10 тыс. руб. в месяц. Выборочное обследование доходов 10 человек дало средний доход 20 тыс. руб. В предположении, что случайная величина дохода имеет распределение Парето вида

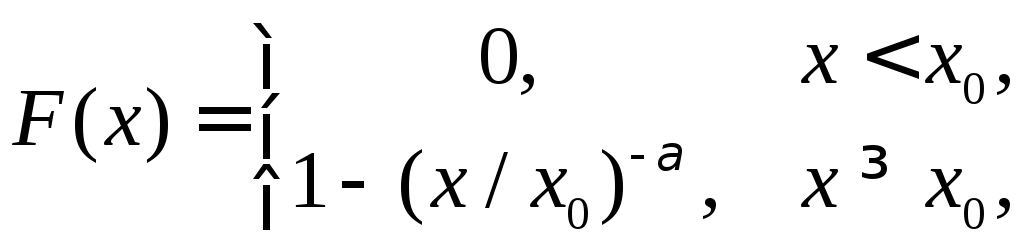
где (тыс. руб.), оценить параметр и средний доход жите­лей методом моментов. Оценить долю жителей с доходами свыше 50 тыс. руб. с использованием метода моментов.

Задача 15. Известно, что некоторая работа занимает время, состоящее из обязательного периода и случайной задержки, распределенной показательно со средним. Хронометраж рабо­чего времени в 10 испытаниях показал среднее время 37 мин. при исправленной выборочной дисперсии 49 мин². Оценить парамет­ры иметодом моментов. Оценить срок, за который работа бу­дет выполнена с вероятностью 99 %, на основе оценки методом моментов.

Задача 16. Прибор состоит из двух блоков – основного и резервного. Если основной блок выходит из строя, включается ре­зервный. Времена службы блоков показательно распределены со средними и. Выборочные испытания для 10 приборов пока­зали средний срок службы 35 часов и среднее квадратическое от­клонение 25 часов. Оценить средние времена службы основного и резервного блоков методом моментов в предположении, что.

Задача 17. В группе людей, имеющих доходы с логнормаль­ным распределением, проведено выборочное обследование. По выборке из 10 человек получен средний доход 9000 руб. при среднем квадратическом отклонении 300 руб. Найти оценки па­раметров а и методом моментов. Оценить долю людей с доходами от 8500 до 9500 руб. с использованием метода моментов.

Задача 18. В таблице приведены сгруппированные данные о коэффициентах соотношения заемных и собственных средств на 100 малых предприятиях региона.

Номер интервала	Интервал	Середина интервала
1	5,05 – 5,15	5,1	5
2	5,15 – 5,25	5,2	8
3	5,25 – 5,35	5,3	12
4	5,35 – 5,45	5,4	20
5	5,45 – 5,55	5,5	26
6	5,55 – 5,65	5,6	15
7	5,65 – 5,75	5,7	10
8	5,75 – 5,85	5,8	4

Оценить долю малых предприятий с коэффициентом не бо­лее 5,5 с применением метода моментов (используя нормальное приближение) и непосредственно по таблице.

Задача 19. В ОТК были измерены диаметры 300 валиков из партии, изготовленной одним станком-автоматом. Отклонения измеренных диаметров от номинала (в мм) даны в таблице.

Границы отклонений	Середина интервала	Число валиков	Границы отклонений	Середина интервала	Число валиков
–30 ... –25	–27,5	3	0 – 5	2,5	55
–25 ... –20	–22,5	8	5 – 10	7,5	30
–20 ... –15	–17,5	15	10 – 15	12,5	25
–15 ... –10	–12,5	35	15 – 20	17,5	14
–10 ... –5	–7,5	40	20 – 25	22,5	8
–5 ... 0	–2,5	60	25 – 30	27,5	7

Оценить долю изделий, для которых отклонение не превосходит 15мм по абсолютной величине, с применением метода мо­ментов (используя нормальное приближение) и непосредственно по таблице.

Задача 20. В таблице представлены данные о числе сделок на фондовой бирже за квартал для 400 инвесторов.

	0	1	2	3	4	5	6	7	8	9	10
	146	97	73	34	23	10	6	3	4	2	2

В предположении, что случайное число сделок описывается распределением Пуассона, оценить параметр методом момен­тов. Оценить вероятность того, что число сделок за квартал будет не менее двух, применяя метод моментов, и непосредственно по таблице.

Задача 21. Для изучения распределения заработной платы работников определенной отрасли обследовано 100 человек. Результаты представлены в таблице.

Зарплата (в долларах)	Число человек	Зарплата (в долларах)	Число человек
190 – 192	1	200 – 202	19
192 – 194	5	202 – 204	11
194 – 196	9	204 – 206	4
196 – 198	22	206 – 208	1
198 – 200	28	208 – 210	0

Оценить долю работников с зарплатой менее 200 долл. на ос­нове оценок методом моментов (используя нормальное прибли­жение) и непосредственно по таблице.

Задача 22. При измерении веса 20 шоколадных батончиков (с номинальным весом 50 г) получены следующие значения (в граммах): 49,1; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51,6; 49,8; 50,1; 49,7; 48,8; 51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.

Оценить долю батончиков с весом менее 49 г на основе оце­нок методом моментов (используя нормальное приближение) и непосредственно по их доле в выборке.

Задача 23. Пассажир, приходящий в случайные моменты вре­мени на автобусную остановку, в течение пяти поездок фиксировал свое время ожидания автобуса: 5,1; 3,7; 1,2; 9,2; 4,8 (мин). Известно, что автобус ходит с интервалами по минут. Оценитьметодом моментов.

Задача 24. В июне ежедневный спрос на мороженое в киоске составляет в среднем 700 порций со средним квадратическим от­клонением 50 порций. Оценить с вероятностью 95% (используя нормальное приближение) количество порций, удовлетворяю­щее потребность в мороженом на 1 день.

Задача 25. Ежедневный спрос на некоторый товар имеет рас­пределение Симпсона на отрезке [а, b]. За 25 рабочих дней спрос составлял в среднем 100 кг с исправленной выборочной диспер­сией 108 кг. Оценить параметры а и b методом моментов. Оце­нить, сколько требуется товара, чтобы удовлетворить ежеднев­ный спрос с вероятностью 90 %.

Задача 26. Рукопись проверяют независимо друг от друга два редактора. Один нашел 70 ошибок, другой – 50, причем 25 най­денных ошибок были одни и те же (т.е. обнаружены обоими ре­дакторами). Оценить число ошибок, которых они еще не нашли.

Задача 27. Найти методом максимального правдоподобия по выборке точечную оценку параметрар геометрическо­го распределения: , где – число испытаний, произведенных до появления события; р – вероятность появле­ния события в одном испытании.

Задача 28. Найти методом максимального правдоподобия оценку параметра для геометрического распределения с вероят­ностью «успеха» , . Доказать ее несмещенность.

Задача 29.   По выборке в случае бино-миального рас­пределения при известном N методом макси­мального правдоподобия найти оценку параметра р. Совпадает ли эта оценка с полученной методом моментов?

Задача 30. Случайная величина равномерно распределена на ,. Найти оценку параметраметодом максимального правдоподобия.

Задача 31. Найти методом максимального правдоподобия оценку параметра а распределения, задаваемого функцией плотности:

Построить несмещенную оценку на основе оценки макси­мального правдоподобия.

Задача 32. Оценить с помощью метода максимального правдоподобия параметр сдвига в сдвинутом экспоненциальном распределении, задаваемом плотностью

Задача 33. Случайная величина подчинена гамма-распре­делению, плотность которого определяется параметрами , и функцией плотности. Найти мето­дом максимального правдоподобия оценкуb (при известном а).

Задача 34. По результатам независимых наблюдений за случайной величинойХ, распределение которой задано плот­ностью , где, найти методом макси­мального правдоподобия оценку параметра.

Задaча 35. Функция распределения случайной величины Х имеет вид . Найти оценку параметраметодом максимального правдоподобия.

Задача 36. В случае сдвинутого показательного распределения ,методом максимального правдоподобия найти оценкиипараметровисоответственно.

Задача 37. По наблюдениям случайной величины с распреде­лением Парето вида

оценить параметр а методом максимального правдоподобия.

Задача 38. По наблюдениям случайной величины с распреде­лением ,оценить параметрметодом максималь­ного правдоподобия.

Задача 39. По наблюдениям случайной величины, равно-мерно распределенной на отрезке , найти оценки пара­метрова и b методом максимального правдоподобия. Найти их математическое ожидание и построить несмещенные оценки.

Задача 40. Случайная величина Х (число появлений события А в n независимых испытаниях) подчинена бино-миальному за­кону распределения с неизвестным параметром р. Ниже приве­дено эмпирическое распределение числа появлений события А в 100 наблюдениях (в первой строке указано число появлений события в одном опыте из n = 10 испытаний; во второй строке приведена частота – число опытов, в которых наблюдалось появлений события А):

	0	1	2	3	4	5	6	7
	2	3	10	22	26	20	12	5

Найти методом максимального правдоподобия точечную оценку неизвестного параметра р биномиального распределе­ния.

Задача 41. Случайная величина Х (время безотказной работы изделия) имеет показательное распределение , где. В таблице приведены сгруппированные данные по времени работы (в часах) для 1000 изделий.

	5	15	25	35	45	55	65
	365	245	150	100	70	45	25

Найти методом максимального правдоподобия точечную оценку неизвестного параметра показательного распределения. Какова вероятность того, что изделие может прослужить более 60 часов?

Задача 42. В поселке Полтинниково все жители имеют доход не менее 5 тыс. руб. в месяц. Выборочное обследование доходов 10 человек дало следующие результаты: 5,4; 6; 5,9; 7,9; 7,1; 9,2; 5,3; 5,4; 7,8; 5,6 (тыс. руб.). В предположении, что случайная величина дохода имеет рас­пределение Парето вида

,

где (тыс. руб.), оценить параметра и средний доход жителей методом максимального правдоподобия. Оценить долю жителей с доходами свыше 10 тыс. руб. на основе оценки максимального правдоподобия.

Задача 43. Известно, что некоторая работа занимает время, состоящее из обязательного периода и случайной задержки, распределенной показательно со средним. Хронометраж рабо­чего времени в 10 случаях дал следующие результаты: 32; 30; 37; 35; 42; 39; 34; 32; 31; 35 (мин). Оценить параметрыиметодом максимального правдоподобия. Оценить срок, за который работа будет выполнена с вероятностью 99 %, на основе оценки макси­мального правдоподобия.

Задача 44. Пассажир, приходящий в случайные моменты вре­мени на автобусную остановку, в течение пяти поездок фикси­ровал свое время ожидания автобуса: 5,1; 3,7; 1,2; 9,2; 4,8 (мин.). Известно, что автобус ходит с интервалами по минут. Оценитьметодом максимального правдоподобия. Вычислить несмещен­ную оценку.

Задача 45. Ежедневный спрос на некоторый товар равномерно распределен на отрезке . За 6 рабочих дней спрос составлял: 104; 80; 96; 120; 113; 82 (кг). Оценитьа и b, используя несмещен­ные оценки на основе оценки максимального правдоподобия. Оценить, сколько товара требуется для удовлетворения ежеднев­ного спроса с вероятностью 90 %.