Задачи для самостоятельного решения
1. Найти значение коэффициента C и плотность распределения f(x) случайной величины X, функция распределения которой имеет вид:
Ответ:
C = 1;
2.
Найти вероятность того, что значение
случайной величины X
принадлежит интервалу (2; 3), если плотность
распределения величины X
задана функцией:
Ответ:0,2.
3. Найти плотность распределения f(x) случайной величины Х, функция распределения которой имеет вид:
Какова вероятность того, что значение случайной величины X принадлежит интервалу (0,5; 1)?
Ответ: P = 0,5.
4.
Найти интегральную
функцию распределения F(x)
и оценить вероятность попадания
непрерывной
случайной величины
X
в интервал (0,5; 1,5), если
плотность распределения величины
X
имеет
вид:
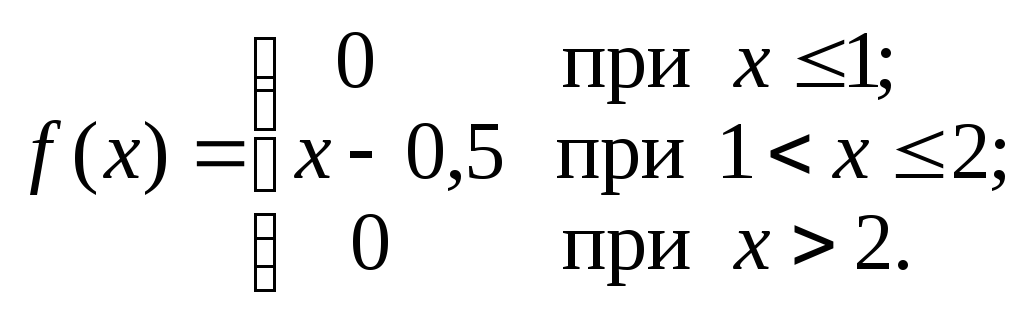
Построить графики функций f(x) и F(x).
Ответ:
P(0,5 <
Х <
1,5) = 0,375.
2.5. Числовые характеристики непрерывных случайных величин
Математическое ожидание непрерывной случайной величины X определяется по следующей формуле:
, (57)
где
.
Дисперсия непрерывной случайной величины X:
, (58)
где
.
Все свойства M(X) и D(X), указанные выше в п. 2.3 для дискретных величин, сохраняются и для непрерывных величин.
Начальный момент порядка k непрерывной случайной величины X вычисляется по формуле
. (59)
Центральный момент порядка k непрерывной случайной величины X, определяется равенством:
. (60)
Если все возможные значения X принадлежат интервалу (a; b), то
;
(61)
. (62)
Пример 2.15. Найти математическое ожидание и дисперсию случайной величины X, которая задана дифференцированной функцией f(x) = 2x в интервале (0; 1), вне его f(x) = 0.
Решение.
.
Пример
2.16. Найти
математическое
ожидание и начальный момент второго
порядка случайной величины X,
заданной интегральной
функцией:
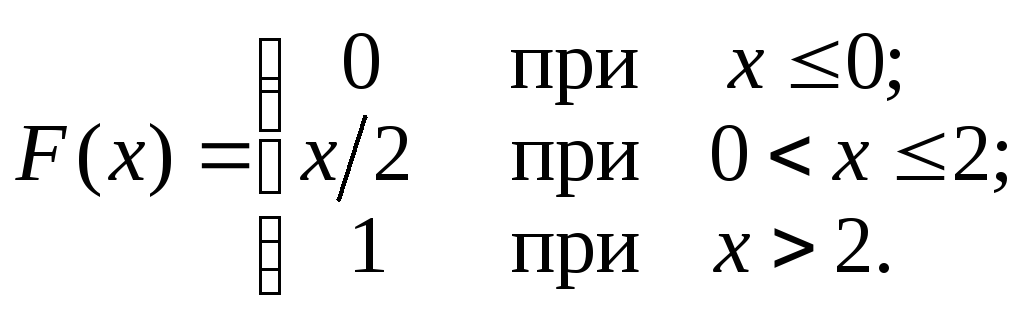
Решение. Найдем дифференциальную функцию X:
Используя
формулу (61) рассчитаем математическое
ожидание:
.
По
формуле (60) найдем начальный момент
второго порядка:
Пример
2.17. Случайная
величина X
задана интегральной функцией распределения:
Необходимо выполнить следующее:
1. Найти плотность вероятности (дифференциальную функцию).
2. Вычислить математическое ожидание и дисперсию X.
3. Найти вероятность того, что X примет значение, принадлежащее интервалу (0,25; 0,5).
4. Построить графики функций F(x) и f(x).
Решение.
1. Найдем функцию плотности вероятности случайной величины X. Согласно формуле (51) плотность вероятности f(x) равна
2. Вычислим математическое ожидание используя формулу (61):
.
Дисперсию величины X рассчитаем по формуле (58):
3.
Согласно формуле (55) вероятность того,
что случайная величина X
примет значение, принадлежащее интервалу
(0,25; 0,5) будет равна:
.
4. Построим графики функций F(x) и f(x). Графики функций F(x) и f(x) отражены на рис. 2.5 и 2.6.
|
Рис. 2.5. График интегральной функции |
Рис. 2.6. График дифференциальной функции |
Задачи для самостоятельного решения
1. Найти дисперсию случайной величины X, заданной следующей интегральной функцией:
Ответ:
.
2.
Найти дисперсию и среднее квадратическое
отклонение случайной величины Х,
которая задана дифференциальной функцией
в интервале (0; 5) и вне его f(x)
= 0.
Ответ:
D(X)
= 110, (X)
=
.
3. Найти начальные и центральные моменты первых трех порядков случайной величины X, которая задана следующей функцией распределения:
Ответ:
;
;
;
;
;
.