2. Случайные величины

2.1. Понятие случайной величины

Случайной величиной называется величина, которая в результате испытания из множества возможных значений принимает одно значение, заранее неизвестное и зависящее от случая.

Случайная величина характеризуется значениями, которыми она может принимать, и вероятностями, с которыми эти значения принимаются.

В отличие от случайного события, которое является качественной характеристикой результата испытания, случайная величина характеризует результат испытания количественно.

Случайные величины могут быть дискретными и непрерывными.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным либо бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Случайные величины будем обозначать заглавными буквами латинского алфавита (X, Y, Z), а их значения – строчными буквами с индексами (например, x₁, x₂, x₃).

Дискретная случайная величина считается заданной, если известны все возможные ее значения и их вероятности.

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих вероятностей.

Закон распределения дискретной случайной величины X может быть задан в виде таблицы, первая строка которой содержит все возможные значения x_i, а вторая – вероятности p_i:

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

.

Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки (x_i, p_i) и соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения.

Закон распределения дискретной случайной величины может быть задан аналитически или с помощью функции распределения.

Распределение дискретной случайной величины идет согласно формуле

P(X=x_i) = φ(x_i). (38)

Пример 2.1. Построить многоугольник распределения, если дискретная случайная величина X имеет следующий закон распределения:

X	0,2	0,4	0,6	0,8	1
P	0,1	0,2	0,4	0,2	0,1

Решение. В прямоугольной системе координат строим точки M₁(0,2;0,1), M₂(0,4;0,2), M₃(0,6;0,4), M₄(0,8;0,2), M₅(1;0,1). Соединяем эти точки отрезками прямых (рис. 2.1). Ломаная M₁M₂M₃M₄M₅ является многоугольником распределения.

Рис. 2.1

Пример 2.2. В коробке 7 карандашей, из которых 4 красных. Из этой коробки наудачу извлекаются 3 карандаша. Найти закон распределения случайной величины X, равной числу красных карандашей в выборке.

Решение. В выборке из трех карандашей может не оказаться ни одного красного карандаша, может появиться 1, 2 или 3 красных карандаша. Поэтому, случайная величина X может принимать только четыре значения: x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3.

Найдем вероятность этих значений:

; ;

; .

Следовательно, случайная величина X имеет следующий закон распределения:

X	0	1	2	3
P

.

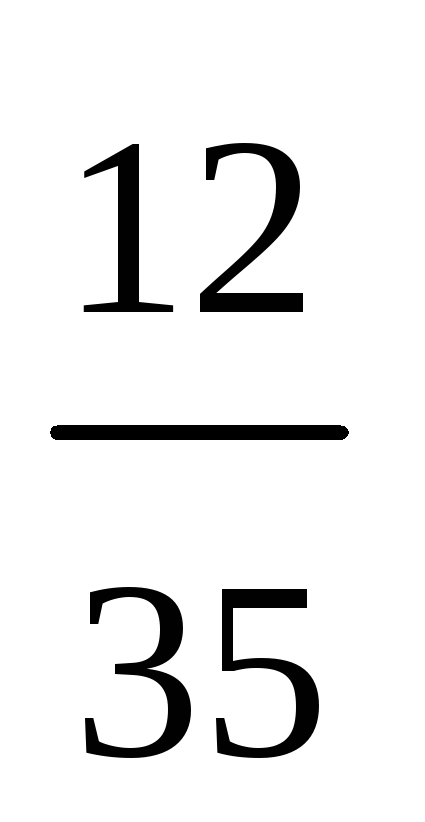
Пример 2.3. В партии товаров 10 % бракованных изделий. Наудачу отобрано 4 изделия. Найти закон распределения случайной величины X – числа бракованных изделий среди 4 отобранных.

Решение. Случайная величина X имеет следующие возможные значения: x₁ = 0 (ни одно из изделий не браковано), x₂ = 1 (одно изделие из 4 браковано), x₃ = 2 (два изделия из 4 бракованы), x₄ = 3 (три изделия из 4 бракованы), x₅ = 4 (все изделия из 4 отобранных бракованы).

Вероятности этих значений рассчитаем по формуле Бернулли (28):

при n = 4: p = 0,1; q = 0,9; k = 0, 1, 2, 3, 4.

P₄(0) = 0,94 = 0,6561; ;

; ;

.

Ряд распределения будет иметь следующий вид:

X	0	1	2	3	4
P	0,6561	0,2916	0,0486	0,0036	0,0001

Аналитический закон распределения в данном примере представлен формулой Бернулли и назван биномиальным.

Если число испытаний n велико и вероятность p появления события A в одном испытании мала, то вероятность P_n(k) того, что событие A появится ровно в k испытаниях, находится по приближенной формуле Пуассона:

, (39)

где λ = np.