
ЭКОНОМЕТРИКА и математическая экономика / Эконометрика. Учебник продвинутый (2005)
.pdf
524 |
|
|
Модели с авторегрессионной условной . . . |
|||
15 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
–5 |
|
|
|
|
|
|
–10 |
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
–15 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
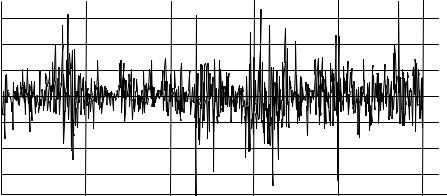
1995–09–21 |
1996–08–26 |
1997–07–22 |
1998–06–18 |
1999–05–14 |
2000–04–07 |
|
Рис. 16.1. Темпы прироста индекса РТС с 21 сентября 1995 г. по 7 апреля 2000 г., в процентах. |
||||||
16.1. Модель ARCH
Модель ARCH, т.е. модель с авторегрессионной условной гетероскедастичностью (autoregressive conditional heteroskedasticity), предложена Р. Энглом в 1982 г. для моделирования кластеризации волатильности. Процесс ARCH q-го порядка, {εt}+t=∞−∞, задается следующими соотношениями:
εt|Ωt−1 N (0, σt2 ), |
|
|
||
σ2 |
= ω + γ1ε2 |
+ . . . + γq ε2 |
. |
(16.1) |
t |
t−1 |
t−q |
|
|
Здесь Ωt−1 = (εt−1 , εt−2, . . . ) — предыстория процесса {εt}, а σt2 |
— услов- |
|||
ная по предыстории дисперсия εt , т.е. σt2 = var(εt|Ωt−1) = E(ε2t |Ωt−1). Условную дисперсию часто называют волатильностью процесса. Для того чтобы условная дисперсия оставалась положительной, требуется выполнение соотношений ω > 0
и γ1, . . . , γq 0. |
|
|
|
Данный процесс можно записать несколько иначе: |
|
||
ξt NID (0, 1), |
|
|
|
εt = ξtσt, |
|
|
|
σ2 = ω + γ1 |
ε2 |
+ . . . + γq ε2 |
. |
t |
t−1 |
t−q |
|
Аббревиатура NID означает, что ξt нормально распределены и независимы. Такая запись удобна тем, что нормированный случайный процесс ξt не зависит от предыстории.
Смысл модели ARCH состоит в том, что если абсолютная величина εt оказывается большой, то это приводит к повышению условной дисперсии в последующие
16.1. Модель ARCH |
525 |
периоды. В свою очередь, при высокой условной дисперсии более вероятно появление больших (по абсолютной величине) значений εt . Наоборот, если значения εt в течение нескольких периодов близки к 0, то это приводит к понижению условной дисперсии в последующие периоды практически до уровня ω. В свою очередь, при низкой условной дисперсии более вероятно появление малых (по абсолютной величине) значений εt . Таким образом, ARCH-процесс характеризуется инерционностью условной дисперсии (кластеризацией волатильности).
Несложно показать, что процесс ARCH не автокоррелирован:
E(εtεt−j ) = E (E(εtεt−j |Ωt−1)) = E (εt−j E(εt|Ωt−1)) = 0.
Поскольку процесс имеет постоянное (нулевое) математическое ожидание и не автокоррелирован, то он является слабо стационарным в случае, если у него есть дисперсия.
Если обозначить разницу между величиной ε2t и ее условным математическим ожиданием, σt2 , через ηt, то получится следующая эквивалентная запись процесса
ARCH:
ε2 |
= ω + γ1 |
ε2 |
+ . . . + γq ε2 |
+ ηt. |
(16.2) |
t |
|
t−1 |
t−q |
|
|
Поскольку условное математическое ожидание ηt равно 0, то безусловное математическое ожидание также равно 0. Кроме того, как можно показать, {ηt} не автокоррелирован. Следовательно, квадраты процесса ARCH(q) следуют авторегрессионному процессу q-го порядка.
Если все корни характеристического уравнения
1 − γ1z − . . . − γq zq = 0
лежат за пределами единичного круга, то у процесса ARCH(q) существует безусловная дисперсия, и он является слабо стационарным. Поскольку коэффициенты γj
неотрицательны, то это условие эквивалентно условию |
q |
γj < 1. |
j=1 |
Действительно, вычислим безусловную дисперсию стационарного ARCHпроцесса, которую мы обозначим через σ2 . Для этого возьмем математическое ожидание от обеих частей уравнения условной дисперсии (16.1):
E(σ2) = ω + γ1E(ε2 |
) + . . . + γq E(ε2 |
). |
||
t |
t−1 |
|
t−q |
|
Заметим, что E σt2 |
= E E(εt2|Ωt−1) = E εt2 |
= var(εt2) = σ2 , т.е. мате- |
||
матическое ожидание условной дисперсии равно безусловной дисперсии. Следовательно,
σ2 = ω + γ1σ2 + . . . + γq σ2,

526 |
|
|
Модели с авторегрессионной условной . . . |
|||||
0.3 |
|
|
|
|
|
ARCH(1),γ1 = 0.7, ω = 1 |
|
|
|
|
|
|
|
|
|
||
0.25 |
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
0.15 |
|
|
|
|
|
N(0;ω / (1Kγ1)) |
|
|
|
|
|
|
|
|
|
||
0.1 |
|
|
|
|
|
|
|
|
0.05 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
K8 |
K6 |
K4 |
K2 |
0 |
2 |
4 |
6 |
8 |
Рис. 16.2. Плотность ARCH(1) и плотность нормального распределения с той же дисперсией |
||||||||
или
σ2 = |
|
|
ω |
|
. |
|
|
|
|
||
|
− γ1 |
− |
|
||
1 |
. . . − γq |
||||
Таким образом, для всех εt безусловная дисперсия одинакова, т.е. имеет место гомоскедастичность. Однако условная дисперсия меняется, поэтому одновременно имеет место условная гетероскедастичность2.
Если не все корни приведенного выше характеристического уравнения лежат
за пределами единичного круга, т.е. если |
q |
1, то безусловная дисперсия не |
γj |
||
|
j=1 |
|
существует, и поэтому ARCH-процесс не будет слабо стационарным3.
Еще одно свойство ARCH-процессов состоит в том, что безусловное распределение εt имеет более высокий куртозис (т.е. более толстые хвосты и острую вершину), чем нормальное распределение (определение куртозиса и эксцесса см. в Приложении A.3.1). У ARCH(1) эксцесс равен
E(ε4) |
|
6γ2 |
|
t |
− 3 = |
1 |
, |
σ4 |
1 − 3γ12 |
2Она называется авторегрессионной, поскольку динамика квадратов ARCH-процесса описывается авторегрессией.
3При этом у ARCH-процессов есть интересная особенность: они могут быть строго стационарны, не будучи слабо стационарны. Дело в том, что определение слабой стационарности требует существования конечных первых и вторых моментов ряда. Строгая же стационарность этого не требует, поэтому даже если условная дисперсия бесконечна (и, следовательно, ряд не является слабо стационарным), ряд все же может быть строго стационарным.

16.2. Модель GARCH |
527 |
причем при 3γ12 1 четвертый момент распределения не существует (эксцесс равен бесконечности). Это свойство ARCH-процессов хорошо соответствует финансовым временным рядам, которые обычно характеризуются толстыми хвостами. На рисунке 16.2 изображен график плотности безусловного распределения ARCH(1). Для сравнения на графике приведена плотность нормального распределения с той же дисперсией.
Получить состоятельные оценки коэффициентов ARCH-процесса можно, используя вышеприведенное представление его квадратов в виде авторегрессии (16.2). Более эффективные оценки получаются при использовании метода максимального правдоподобия.
При применении ARCH-моделей к реальным данным было замечено, что модель ARCH(1) не дает достаточно длительных кластеров волатильности, а только порождает большое число выбросов (выделяющихся наблюдений). Для корректного описания данных требуется довольно большая длина лага q, что создает трудности при оценивании. В частности, зачастую нарушается условие неотрицательности оценок коэффициентов γj . Поэтому Энгл предложил использовать модель со следующими ограничениями на коэффициенты лага: они задаются с помощью весов вида:
wj = q + 1 − j ,
0.5q(q + 1)
сумма которых равна 1 и которые линейно убывают до нуля. Сами коэффициенты берутся равными γj = γwj . Получается модель с двумя параметрами, ω и γ:
σ2 |
= ω + γ w1 |
ε2 |
+ . . . + wq ε2 |
. |
t |
|
t−1 |
t−q |
|
16.2. Модель GARCH
Модель GARCH (generalized ARCH — обобщенная модель ARCH), предложенная Т. Боллерслевом, является альтернативной модификацией модели ARCH (16.2), позволяющей получить более длинные кластеры при малом числе параметров. Модель ARMA зачастую позволяет получить более сжатое описание временных зависимостей для условного математического ожидания, чем модель AR. Подобным же образом модель GARCH дает возможность обойтись меньшим количеством параметров по сравнению с моделью ARCH, если речь идет об условной дисперсии. В дальнейшем мы проведем прямую аналогию между моделями GARCH
и ARMA.
528 |
Модели с авторегрессионной условной . . . |
Для того чтобы вывести модель GARCH, используем в модели ARCH бесконечный геометрический лаг:
|
|
∞ |
|
|
|
|
γ |
|
|
|
σ2 |
= ω + γ |
δj−1ε2 |
= ω + |
|
|
|
|
ε2 |
. |
|
1 |
|
|
|
|||||||
t |
|
t−j |
|
|
− |
δL t−1 |
|
|||
|
j=1 |
|
|
|
|
|
|
|||
Применяя преобразование Койка, получим |
|
|
|
|
|
|
|
|
||
|
σt2 = (1 − δ)ω + δσt2−1 + γεt2−1. |
|
||||||||
Поменяв очевидным образом обозначения, получим модель GARCH(1, 1): |
||||||||||
|
σ2 |
= ω + δσ2 |
|
+ γε2 |
|
|
. |
|
|
|
|
t |
t−1 |
t−1 |
|
|
|
|
|||
Модель GARCH(p, q) обобщает эту формулу:
σ2 |
= ω + δ1σ2 |
+ . . . + δpσ2 |
+ γ1ε2 |
+ . . . + γq ε2 |
|
= |
|
|
|
|
t |
t−1 |
t−p |
t−1 |
p |
t−q |
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
= ω + |
δj σ2 |
+ |
γj ε2 |
. (16.3) |
||
|
|
|
|
|
|
|
t−j |
|
t−j |
|
|
|
|
|
j=1 |
|
|
|
j=1 |
|
|
При этом предполагается, что ω > 0, δ1, . . . , δp 0 и |
γ1, . . . , γq 0. |
|||||||||
На практике, как правило, достаточно взять p =1 и |
|
q =1. Изредка используют |
||||||||
GARCH(1, 2) или GARCH(2, 1).
Как и в модели ARCH, σt2 служит условной дисперсией процесса:
εt|Ωt N (0, σt2 ).
Рассчитаем безусловную дисперсию GARCH-процесса, предполагая, что он стационарен. Для этого возьмем математические ожидания от обеих частей уравнения 16.3 для условной дисперсии:
p |
|
|
q |
|
E(σ2) = |
δj E(σ2 |
) + |
γj E(ε2 |
), |
t |
t−j |
|
t−j |
|
j=1 |
|
|
j=1 |
|
откуда
pq
σ2 = δj σ2 + γj σ2
|
j=1 |
j=1 |
|
|
и |
|
|
|
|
σ2 = |
|
1 |
. |
|
|
|
|||
p |
q |
|||
|
|
1 − δj − γj
j=1 j=1

16.2. Модель GARCH |
529 |
Таким образом, с точки зрения безусловной дисперсии GARCH-процесс гомоскедастичен.
Для того чтобы дисперсия была конечной, необходимо выполнение условия
pq
δj + |
γj < 1. В частности, для модели GARCH(1, 1) требуется δ1 + γ1 < 1. |
|
j=1 |
j=1 |
|
Процесс GARCH можно записать в эквивалентной форме, если, как и выше, |
||
в уравнении 16.2 для модели ARCH, обозначить ηt = εt2 − σt2 : |
||
|
m |
p |
|
εt2 = ω + (δj + γj )εt2−j + ηt − δj ηt−j , |
|
|
j=1 |
j=1 |
где m = max(p, q). (В этой записи подразумевается δj = 0 при j > p и γj = 0 при j > q.) Такая форма записи позволяет увидеть, что квадраты GARCH-процесса подчиняются модели ARMA(m, p).
Этот факт дает возможность получить автокорреляционную функцию квадратов GARCH-процесса. В частности, для GARCH(1, 1) автокорреляционная функция
квадратов имеет вид |
|
|
ρ1 = |
γ1(1 − δ12 − δ1γ1) |
, |
|
1 − δ12 − 2δ1γ1 |
|
ρτ = (δ1 + γ1)τ −1ρτ −1, τ > 1.
Условие существования безусловного четвертого момента у отдельного наблю-
дения процесса GARCH(1, 1) состоит в том, что 3γ2 |
+ 2γ1δ1 |
+ δ2 |
< 1. Если это |
||||
|
|
|
1 |
|
|
1 |
|
условие выполняется, то эксцесс равен |
|
|
|
|
|||
|
E(ε4) |
|
6γ2 |
|
|
|
|
|
t |
− 3 = |
1 |
|
|
|
|
|
σ4 |
1 − δ12 − 2δ1 γ1 − 3γ12 |
|
|
|
||
и является положительным. То есть GARCH-процесс (как и его частный случай — ARCH-процесс) имеет более высокий куртозис, чем нормальное распределение. В то же время, безусловное распределение отдельного наблюдения GARCHпроцесса является симметричным, поэтому все нечетные моменты, начиная с третьего, равны нулю.
Стандартным методом оценивания для моделей GARCH является метод максимального правдоподобия. Условно по предыстории Ωt−1 отдельное наблюдение GARCH-процесса распределено нормально: εt|Ωt−1 N (0, σt2 ). Функция правдоподобия для ряда ε1, . . . , εT , подчиняющегося GARCH-процессу, вычисляется как произведение плотностей этих условных нормальных распределений:
T |
1 |
|
|
ε2 |
||
L = |
|
|
exp |
− |
t |
|
|
|
|
. |
|||
|
|
2σt2 |
||||
2 |
||||||
t=1 |
|
2πσt |
|
|
|
|

530 |
Модели с авторегрессионной условной . . . |
Максимизируя эту функцию правдоподобия по неизвестным параметрам, получим оценки максимального правдоподобия для GARCH-процесса.
При оценивании условную дисперсию σt2 следует считать функцией параметров модели и вычислять по рекуррентной формуле 16.3. Для этих вычислений требуются «довыборочные» значения самого процесса и его условной дисперсии, а они неизвестны. Для решения этой проблемы можно использовать различные приемы. Самый простой, по-видимому, состоит в том, чтобы заменить условные дисперсии в начале ряда ( t = 1, . . . , m) оценкой безусловной дисперсии, т.е. величиной
T
s2 = T1 t=1 ε2t .
Оценки максимального правдоподобия являются состоятельными и асимптотически эффективными.
На практике модель GARCH дополняют какой-либо моделью, описывающей поведение условного или безусловного математического ожидания наблюдаемого ряда. Например, можно предположить, что наблюдается не εt, а εt плюс константа, т.е. что наблюдаемый ряд {xt} имеет постоянное безусловное математическое ожидание β, к которому добавляется ошибка εt в виде процесса
GARCH:
xt = β + εt.
Можно моделировать безусловное математическое ожидание с помощью линейной регрессии, т.е.
xt = Ztα + εt.
Это позволяет учитывать линейный тренд, детерминированные сезонные переменные и т.п. При оценивании в функции правдоподобия вместо εt используют xt − Ztα.
С точки зрения прогнозирования перспективной является модель, сочетающая ARIMA с GARCH. Модель ARIMA в этом случае используется для моделирования поведения условного математического ожидания ряда, а GARCH — для моделирования условной дисперсии.
Важнейший вывод, который следует из анализа модели ARCH, состоит в том, что наблюдаемые изменения в дисперсии (волатильности) временного ряда могут иметь эндогенный характер, то есть порождаться определенной нелинейной моделью, а не какими-то внешними структурными сдвигами.
16.3. Прогнозы и доверительные интервалы для модели GARCH |
531 |
16.3.Прогнозы и доверительные интервалы для модели GARCH
Одна из важнейших целей эконометрических моделей временных рядов — построение прогнозов. Какие преимущества дают модели с авторегрессионной условной гетероскедастичностью с точки зрения прогнозирования временных рядов по сравнению с моделями линейной регрессии или авторегрессии — скользящего среднего? Оказывается, что прямых преимуществ нет, но есть ряд опосредованных преимуществ, которые в отдельных случаях могут иметь большое значение.
Рассмотрим модель линейной регрессии
xt = Ztα + εt, t = 1, . . . , T ,
вкоторой ошибка представляет собой GARCH-процесс. Поскольку ошибки не автокоррелированы и гомоскедастичны, то, как известно, оценки наименьших квадратов являются наилучшими в классе линейных по x несмещенных оценок. Однако наличие условной гетероскедастичности позволяет найти более эффективные (т.е. более точные) оценки среди нелинейных и смещенных оценок. Действительно, метод максимального правдоподобия дает асимптотически эффективные оценки, более точные, чем оценки МНК. В ошибку прогноза вносит свой вклад, во-первых, ошибка εT +1 , а во-вторых, разница между оценками параметров и истинными значениями параметров. Использование более точных оценок позволяет уменьшить
внекоторой степени вторую составляющую ошибки прогноза.
Вобычных моделях временного ряда с неизменными условными дисперсиями (например, ARMA) неопределенность ошибки прогноза — это возрастающая функция горизонта прогноза, которая (если не учитывать разницу между оценками параметров и истинными значениями параметров, отмеченную в предыдущем абзаце) не зависит от момента прогноза. Однако в присутствии ARCH-ошибок точность прогноза будет нетривиально зависеть от текущей информации и, следовательно, от момента прогноза. Поэтому для корректного построения интервальных прогнозов требуется иметь оценки будущих условных дисперсий ошибки.
Кроме того, в некоторых случаях полезно иметь прогнозы не только (условного) математического ожидания изучаемой переменной, но и ее (условной) дисперсии. Это важно, например, при принятии решений об инвестициях в финансовые активы. В этом случае дисперсию (волатильность) доходности естественно рассматривать как меру рискованности финансового актива. Таким образом, сами по себе прогнозы условной дисперсии могут иметь практическое применение.
Покажем, что доверительный интервал прогноза зависит от предыстории
ΩT = (xT , xT −1, . . . , x1, . . . ).
532 |
Модели с авторегрессионной условной . . . |
Реально прогноз делается на основе имеющегося ряда (x1, . . . , xT ), а не всей предыстории, однако различие это не столь существенно. При этом мы будем исходить из того, что нам известны истинные параметры процесса. Прогноз на τ периодов — это математическое ожидание прогнозируемой величины xT +τ , условное относительно имеющейся на момент t информации ΩT . Он равен
xT (τ ) = E(xT +τ |ΩT ) = E(ZT +τ α + εT +τ |ΩT ) = ZT +τ α.
Здесь учитывается, что поскольку информация ΩT содержится в информации ΩT +τ −1 при τ 1, то по правилу повторного взятия математического ожидания выполнено
E(εT +τ |ΩT ) = E (E (εT +τ |ΩT +τ −1) |ΩT ) = E(0|ΩT ) = 0.
Таким образом, если известны истинные параметры, присутствие GARCH-ошибок не отражается на том, как строится точечный прогноз, — он оказывается таким же, как для обычной линейной регрессии. Ошибка предсказания в момент времени T на τ шагов вперед
dT (τ ) = xT +τ − xT (τ ) = εT +τ .
Условная дисперсия ошибки предсказания равна
σp2 = E d2T (τ ) ΩT = E ε2T +τ ΩT .
Из этого следует, что она зависит как от горизонта прогноза τ , так и от предыстории ΩT .
Заметим, что при t > T выполнено E εt2|ΩT |
= E σt2|ΩT , поскольку |
E εt2 − σt2 ΩT = E E εt2 − σt2 Ωt−1 |
ΩT = E(0|ΩT ) = 0. |
Учитывая, что E ε2t − σt2|Ωt−1 = 0 и информация ΩT содержится в информации Ωt−1 при t > T , применяем правило повторного взятия математического ожидания:
σp2 = E ε2T +τ |ΩT = E σT2 +τ |ΩT .
Таким образом, фактически дисперсия прогноза xT +τ — это прогноз волатильности на τ шагов вперед.
Возьмем от обеих частей рекуррентного уравнения (16.3) для GARCH-процесса математическое ожидание, условное относительно ΩT . Получим
p |
q |
|
E σt2|ΩT = ω + δj E σt2−j |ΩT + |
γj E εt2−j |ΩT . |
(16.4) |
j=1 |
j=1 |
|
