ЭКОНОМЕТРИКА и математическая экономика / Эконометрика. Учебник продвинутый (2005)

434 Глава 14. Линейные стохастические модели ARIMA

Можно также применить общую формулу для автоковариаций в модели линейного фильтра (14.3) с k = 0:

При |ϕ| 1 дисперсия процесса {xt}, вычисляемая по этой формуле, неограниченно растет.

3) Коэффициент автоковариации k-го порядка по формуле (14.3) равен

Можно вывести ту же формулу иным способом. Ошибка εt некоррелирована не только с xt−1, но и с xt−2, xt−3 и т.д. Поэтому, умножая уравнение процесса (14.8) на xt−k при k > 0 и беря математическое ожидание от обеих частей, получим

E(xtxt−k ) = ϕE(xt−1xt−k )

или

γk = ϕγk−1, k > 0.

Таким образом, учитывая (14.10), получим

σ2

γk = γ0ϕk = ε ϕk . (14.11)

1 − ϕ2

4) Коэффициент автокорреляции, исходя из (14.11), равен:

ρk = γk = ϕk . γ0

При 0 < ϕ < 1 автокорреляционная функция имеет форму затухающей экспоненты (рис. 14.1а), при −1 < ϕ < 0 — форму затухающей знакопеременной экспоненты (рис. 14.1б).

Если ϕ > 1, процесс Маркова превращается во «взрывной» процесс.

В случае ϕ = 1 имеет место так называемый процесс случайного блуждания, который относится к разряду нестационарных.

k k

1

–1

Рис. 14.1

Процесс Юла

Процессом Юла называют авторегрессию второго порядка AR(2):

или, через лаговый оператор:

(1 − ϕ1L − ϕ2L2)xt = εt.

Для стационарности процесса авторегрессии AR(2) необходимо, чтобы корни λ1, λ2 характеристического уравнения

1 − ϕ1z − ϕ2z2 = 0,

которые, вообще говоря, могут быть комплексными, находились вне единичного круга на комплексной плоскости, т.е. |λ1| > 1, |λ2| > 1.

Неформально обоснуем условия стационарности AR(2), разложив характеристический полином ϕ(z) на множители (по теореме Виета λ1λ2 = −1 ϕ2 ):

Для того чтобы процесс vt был стационарным, коэффициент G1 по модулю должен быть меньше единицы, т.е. |λ1| > 1.

С другой стороны, из (14.14) следует, что xt имеет вид процесса Маркова с ошибкой vt :

xt = G2xt−1 + vt.

Условие стационарности такого процесса имеет аналогичный вид: |λ2| > 1.

Приведенные рассуждения не вполне корректны, поскольку vt не является белым шумом. (Укажем без доказательства, что из стационарности vt следует стационарность xt .) Кроме того, корни λ1, λ2 могут быть, вообще говоря, комплексными, что требует изучения свойств комплексного марковского процесса. Более корректное обоснование приведенного условия стационарности будет получено ниже для общего случая AR(p).

Условия стационарности процесса AR(2), |λ1| > 1, |λ2| > 1, можно переписать в эквивалентном виде как ограничения на параметры уравнения авторегрессии:

обязательно лежит вне отрезка [−1, 1]. Для того чтобы и второй корень не попал в этот отрезок, необходимо и достаточно, чтобы значения характеристического полинома ϕ(L) = 1 − ϕ1L − ϕ2L2 в точках −1 и 1 были одного знака. Это условие можно описать неравенством:

ϕ(−1) · ϕ(1) > 0, или (1 + ϕ1 − ϕ2)(1 − ϕ1 − ϕ2) > 0.

можно вывести формулу автокорреляционной функции. Умножив обе части уравнения на xt−k :

xt−k xt = ϕ1xt−k xt−1 + ϕ2xt−k xt−2 + . . . + ϕpxt−k xt−p + xt−k εt,

и перейдя к математическим ожиданиям, получим уравнение, связывающее коэффициенты автоковариации различного порядка:

Это выражение является следствием того, что соответствующие кроссковариации между процессом и ошибкой равны нулю: E(xt−k εt) = 0 при k > 0, т.к. xt−k может включать лишь ошибки εj для j t − k.

Делением уравнения (14.17) на γ0 получаем важное рекуррентное соотношение для автокорреляционной функции:

Подставляя в выражение (14.18) k = 1, . . . , p, получаем, с учетом симметричности автокорреляционной функции, так называемые уравнения Юла—Уокера (Yule—Walker) для AR(p):

ρ1 = ϕ1 + ϕ2ρ1 + . . . + ϕpρp−1,

ρ2 = ϕ1ρ1 + ϕ2 + . . . + ϕpρp−2,

(14.19)

· · ·

ρp = ϕ1ρp−1 + ϕ2ρp−2 + . . . + ϕp.

Мы имеем здесь p линейных уравнений, связывающих p автокорреляций, ρ1, . . . , ρp. Из этой системы при данных параметрах можно найти автокорреляции. С другой стороны, при данных автокорреляциях из уравнений Юла—Уокера можно найти параметры ϕ1, . . . , ϕp. Замена теоретических автокорреляций выборочными дает метод оценивания параметров процесса AR(p).

В частности, для процесса Юла получим из (14.19)

Зная ρ1, . . . , ρp, все последующие автокорреляции ρk ( k > p) можем найти по рекуррентной формуле (14.18).

Для нахождения автоковариационной функции требуется знать γ0, дисперсию процесса xt. Если умножить обе части (14.16) на εt и взять математические ожидания, получим, что E(εtxt) = E(ε2t ) = σε2 . Далее, умножая обе части (14.16) на xt и беря математические ожидания, получим

γ0 = ϕ1γ1 + ϕ2γ2 + . . . + ϕpγp + σε2.

Автоковариации затем можно вычислить как γj = ρj σx2 .

С учетом полученного дополнительного уравнения можно записать вариант уравнений Юла—Уокера для автоковариаций:

γp = ϕ1γp−1 + ϕ2γp−2 + . . . + ϕpγ0.

В этой системе имеется p + 1 уравнений, связывающих p + 1 автоковариацию, что позволяет непосредственно вычислять автоковариации при данных параметрах.

Заметим, что 14.17 и 14.18 имеют вид линейных однородных конечноразностных уравнений, а для подобных уравнений существует общий метод нахождения решения. Решив уравнение 14.18, можно получить общий вид автокорреляционной функции процесса авторегрессии. Проведем это рассуждение более подробно для процесса Юла, а затем рассмотрим общий случай AR(p).

Вывод формулы автокорреляционной функции процесса Юла

Из соотношения (14.18) для p = 2 получаем:

или, используя лаговый оператор, который в данном случае действует на k, ϕ(L)ρk = 0, где ϕ(z) = 1 − ϕ1z − ϕ2z2 — характеристический полином процесса Юла. Как мы видели, этот характеристический полином можно представить в виде:

В свою очередь, из (14.24), с учетом того, что ρ0 = 1 и ρ1 = ϕ1(1 − ϕ2), следует, что

Возвращаясь к формуле (14.24), имеем, исходя из рекуррентности соотношения:

ρk = G2ρk−1 + ωk = G2(G2ρk−2 + ωk−1) + ωk = . . . =

причем A1 + A2 = 1.

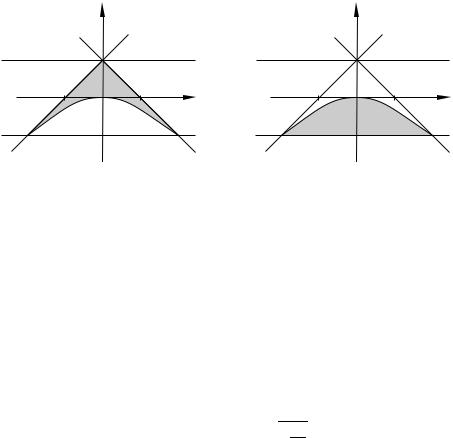
В стационарных процессах корни характеристического уравнения лежат вне единичного круга. Следовательно, |G1| < 1 и |G2| < 1, и автокорреляционная функция состоит из совокупности затухающих экспонент, что на рисунке 14.3

соответствует областям 1, 2, 3 и 4, лежащим выше параболической границы

ϕ21 + 4ϕ2 0.

При этом, если оба корня положительны или доминирует по модулю отрицательный корень (соответственно, положительное G), автокорреляционная функция затухает, асимптотически приближаясь к экспоненте (области 1 и 4 на рис. 14.3). Когда же оба корня отрицательны или доминирует по модулю положительный корень (или отрицательное G), автокорреляционная функция затухает по экспоненте знакопеременно (области 2 и 3 на рис. 14.3).

Если корни разного знака и совпадают по модулю, то затухание ρk происходит в области положительных значений, но имеет колебательный характер:

G1 = −G2 , следовательно A1 = A2 = 0.5 и

Тогда автокорреляционная функция процесса авторегрессии второго порядка будет представлять собой затухающую синусоиду:

ρk = dk · sin(kα + β) , sin β

Подтвердим справедливость формулы. Поскольку коэффициенты характеристического многочлена — действительные числа, то λ1 и λ2 — комплексносопряженные, поэтому G1 и G2 тоже являются комплексно-сопряженными. Далее, G1, как и любое комплексное число, можно представить в виде:

G1 = deiα = d cos α + i d sin α,

где d = |G1| ( = |G2|) — модуль, а α — аргумент комплексного числа G1 . Соответственно, для G2 как для сопряженного числа верно представление:

Пусть β — такой угол, что

1 + d2

tg β = 1 − d2 tg α.

Тогда

Отсюда найдем A2 :

e−iβ

A2 = 1 − A1 = −eiβ − e−iβ .