
ЭКОНОМЕТРИКА и математическая экономика / Эконометрика. Учебник продвинутый (2005)
.pdf554 |
Интегрированные процессы... |
К неформальным методам проверки стационарности можно отнести визуальный анализ графиков спектральной плотности и автокорреляционной функции.
В настоящее время самым популярным из формальных критериев является критерий, разработанный Дики и Фуллером (DF-тест).
Предположим, нужно выяснить, какой из двух процессов лучше подходит для описания временного ряда:
xt = µ0 + µ1t + εt или xt = µ0 + xt−1 + εt,
где εt — стационарный ARMA-процесс. Первый из процессов является стационарным относительно тренда, а второй содержит единичный корень и дрейф. Каждый из вариантов может рассматриваться как правдоподобная модель экономического процесса.
Внешне два указанных процесса сильно различаются, однако можно показать, что оба являются частными случаями одного и того же процесса:
xt = γ0 + γ1t + vt, vt = ϕvt−1 + εt,
что можно переписать также в виде
(xt − γ0 − γ1t) = ϕ(xt−1 − γ0 − γ1(t − 1)) + εt. |
(17.3) |
Как было показано ранее (17.2) для марковского процесса, при |ϕ| < 1 данный процесс эквивалентен процессу xt = µ0 + µ1t + εt , где коэффициенты связаны соотношениями:
γ0 = |
µ0 |
− |
ϕµ1 |
и |
γ1 = |
µ1 |
. |
1 − ϕ |
(1 − ϕ)2 |
1 − ϕ |
|||||
При ϕ = 1 получаем |
|
|
|
|
|
|
|
xt − γ0 − γ1t = xt−1 − γ0 − γ1t + γ1 + εt,
т.е.
xt = γ1 + xt−1 + εt.
Таким образом, как и утверждалось, обе модели являются частными случаями одной и той же модели (17.3) и соответствуют случаям |ϕ| < 1 и ϕ = 1.
Модель (17.3) можно записать следующим образом:
xt = γ0 + γ1t + ϕ(xt−1 − γ0 − γ1(t − 1)) + εt.
17.4. Проверка на наличие единичных корней |
555 |
Это модель регрессии, нелинейная по параметрам. Заменой переменных мы можем свести ее к линейной модели:
xt = µ0 + µ1t + ϕxt−1 + εt,
где µ0 = (1 − ϕ)γ0 + ϕγ1, µ1 = (1 − ϕ)γ1 .
Эта новая модель фактически эквивалентна (17.3), и метод наименьших квадратов даст ту же самую оценку параметра ϕ. Следует, однако, иметь в виду, что линейная модель скрывает тот факт, что при ϕ = 1 будет выполнено µ1 = 0.
Базовая модель, которую использовали Дики и Фуллер, — авторегрессионный процесс первого порядка:
xt = ϕxt−1 + εt. |
(17.4) |
При ϕ = 1 это случайное блуждание. Конечно, вряд ли экономическая переменная может быть описана процессом (17.4). Более реалистично было бы предположить наличие в этом процессе константы и тренда (линейного или квадратичного):
xt |
= µ0 |
+ ϕxt−1 + εt, |
|
|
(17.5) |
||||
xt |
= µ0 |
+ µ1t + ϕxt−1 + εt, |
|
(17.6) |
|||||
x |
t |
= µ |
0 |
+ µ |
t + µ |
t2 + ϕx |
t−1 |
+ ε . |
(17.7) |
|
|
1 |
2 |
|
t |
|
|||
Нулевая гипотеза в критерии Дики—Фуллера состоит в том, что ряд нестационарен и имеет один единичный корень ϕ = 1, при этом µi = 0, альтернативная — в том, что ряд стационарен |ϕ| < 1:
H0 : ϕ = 1, µi = 0,
HA : |ϕ| < 1.
Здесь i = 0, если оценивается (17.5), i = 1, если оценивается (17.6), и i = 2, если оценивается (17.7).
Предполагается, что ошибки εt некоррелированы. Это предположение очень важно, без него критерий работать не будет.
Для получения статистики, с помощью которой можно было бы проверить нулевую гипотезу, Дики и Фуллер предложили оценить данную авторегрессионную модель и взять из нее обычную t-статистику для гипотезы о том, что ϕ = 1 . Эту статистику называют статистикой Дики—Фуллера и обозначают DF. При этом критерий является односторонним, поскольку альтернатива ϕ > 1, соответствующая взрывному процессу, не рассматривается.
DF заключается в том, что с помощью одной t-статистики как бы проверяется гипотеза сразу о двух коэффициентах. На самом деле, фактически подразумевается модель вида (17.3), в которой проверяется гипотеза об одном коэффициенте ϕ.
556 |
Интегрированные процессы... |
Если в регрессии (17.6) нулевая гипотеза отвергается, то принимается альтернативная гипотеза — о том, что процесс описывается уравнением (17.6) с ϕ < 1, то есть это стационарный относительно линейного тренда процесс. В противном случае имеем нестационарный процесс, описываемый уравнением (17.5), где ϕ = 1, то есть случайное блуждание с дрейфом, но без временного тренда в уравнении авторегрессии.
Часто встречается несколько иная интерпретация этой особенности данного критерия: проверяется гипотеза H0 : ϕ = 1 против гипотезы HA : ϕ < 1, и оцениваемая регрессия не совпадает с порождающим данные процессом, каким он предполагается согласно альтернативной гипотезе, а именно, в оцениваемой регрессии имеется «лишний» детерминированный регрессор. Так, чтобы проверить нулевую гипотезу для процесса вида (17.5), нужно построить регрессию (17.6) или (17.7). Аналогично для проверки нулевой гипотезы о процессе вида (17.6) нужно оценить регрессию (17.7). Однако приведенная ранее интерпретация более удачная.
Поскольку статистика Дики—Фуллера имеет нестандартное распределение, для ее использования требуются специальные таблицы. Эти таблицы были составлены эмпирически методом Монте-Карло. Все эти статистики получены на основе одного и того же процесса вида (17.4) с ϕ = 1, но с асимптотической точки зрения годятся и для других процессов, несмотря на наличие мешающих параметров, которые приходится оценивать.
Чтобы удобно было использовать стандартные регрессионные пакеты, уравнения регрессии преобразуются так, чтобы зависимой переменной была первая разность. Например, в случае (17.4) имеем уравнение
∆xt = δxt−1 + εt,
где δ = ϕ − 1. Тогда нулевая гипотеза примет вид δ = 0.
Предположение о том, что переменная следует авторегрессионному процессу первого порядка и ошибки некоррелированы, является, конечно, слишком ограничительным. Критерий Дики—Фуллера был модифицирован для авторегрессионных процессов более высоких порядков и получил название дополненного критерия Дики—Фуллера (augmented Dickey—Fuller test, ADF).
Базовые уравнения для него приобретают следующий вид:
k |
|
∆xt = (ϕ − 1)xt−1 + γj ∆xt−j + εt, |
(17.8) |
j=1 |
|
17.4. Проверка на наличие единичных корней |
557 |
||
|
k |
γj ∆xt−j + εt, |
|
∆xt = µ0 |
+ (ϕ − 1)xt−1 + |
(17.9) |
|
|
j=1 |
|
|
|
+ µ1t + (ϕ − 1)xt−1 |
k |
|
∆xt = µ0 |
+ γj ∆xt−j + εt, |
(17.10) |
|
|
|
j=1 |
|
|
|
k |
|
∆xt = µ0 |
+ µ1t + µ2t2 + (ϕ − 1)xt−1 + γj ∆xt−j + εt. |
(17.11) |
|
j=1
Распределения этих критериев асимптотически совпадают с соответствующими обычными распределениями Дики—Фуллера и используют те же таблицы. Грубо говоря, роль дополнительной авторегрессионной компоненты сводится к тому, чтобы убрать автокорреляцию из остатков. Процедура проверки гипотез не отличается от описанной выше.
Как показали эксперименты Монте-Карло, критерий Дики—Фуллера чувствителен к наличию процесса типа скользящего среднего в ошибке. Добавление в число регрессоров распределенного лага первой разности (с достаточно большим значением k) частично снимает эту проблему.
На практике решающим при использовании критерия ADF является вопрос о том, как выбирать k — порядок AR-процесса в оцениваемой регрессии. Можно предложить следующие подходы.
1)Выбирать k на основе обычных t- и F -статистик. Процедура состоит в том, чтобы начать с некоторой максимальной длины лага и проверять вниз, используя t- или F -статистики для значимости самого дальнего лага (лагов). Процесс останавливается, когда t-статистика или F -статистика значимы.
2)Использовать информационные критерии Акаике и Шварца. Длина лага
сминимальным значением информационного критерия предпочтительна.
3)Сделать остатки регрессии ADF-критерия как можно более похожими на белый шум. Это можно проверить при помощи критерия на автокорреляцию. Если соответствующая статистика значима, то лаг выбран неверно и следует увеличить k.
Поскольку дополнительные лаги не меняют асимптотические результаты, то лучше взять больше лагов, чем меньше. Однако этот последний аргумент верен только с асимптотической точки зрения. ADF может давать разные результаты в зависимости от того, каким выбрано количество лагов. Даже добавление лага, который «не нужен» согласно только что приведенным соображениям, может резко изменить результат проверки гипотезы.
Особую проблему создает наличие сезонной компоненты в переменной. Если сезонность имеет детерминированный характер, то достаточно добавить в регрес-
558 |
Интегрированные процессы... |
сию фиктивные сезонные переменные — это не изменяет асимптотического распределения ADF-статистики. Для случая стохастической сезонности также есть специальные модификации критерия.
До сих пор рассматривались критерии I(1) против I(0). Временной ряд может быть интегрированным и более высокого порядка. Несложно понять, что критерии I(2) против I(1) сводятся к рассмотренным, если взять не уровень исследуемого ряда, а первую разность. Аналогичный подход рекомендуется для более высоких порядков интегрирования.
Имитационные эксперименты, проведенные Сэдом и Дики, показали, что следует проверять гипотезы последовательно, начиная с наиболее высокого порядка интегрирования, который можно ожидать априорно. То есть сначала следует проверить гипотезу о том, что ряд является I(2), и лишь после этого, если гипотеза отвергнута, что он является I(1).
17.5.Коинтеграция. Регрессии с интегрированными переменными
Как уже говорилось выше, привычные методы регрессионного анализа не подходят, если переменные нестационарны. Однако не всегда при применении МНК имеет место эффект ложной регрессии.
Говорят, что I(1)-процессы {x1t} и {x2t} являются коинтегрированными порядка 1 и 0, коротко CI(1, 0), если существует их линейная комбинация, которая является I(0), т.е. стационарна. Таким образом, процессы {x1t} и {x2t}, интегрированные первого порядка I(1), — коинтегрированы, если существует коэффициент λ такой, что x1t − λx2t I(0). Понятие коинтеграции введено Грейнджером в 1981 г. и использует модель исправления ошибок. Коинтегрированные процессы {x1t} и {x2t} связаны между собой долгосрочным стационарным соотношением, и предполагается, что существует некий корректирующий механизм, который при отклонениях возвращает x1t и x2t к их долгосрочному отношению.
Если λ = 1, то разность x1t −x2t будет стационарной и, грубо говоря, x1t и x2t будут двигаться «параллельно» во времени. На рисунке 17.2 изображены две такие коинтегрированные переменные, динамика которых задана моделью исправления ошибок:
∆x1t = −0.2(x1,t−1 − x2,t−1 + 2) + ε1t, |
(17.12) |
∆x2t = 0.5(x1,t−1 − x2,t−1 + 2) + ε2t, |
(17.13) |
где ε1t и ε2t — независимые случайные величины, имеющие стандартное нормальное распределение.
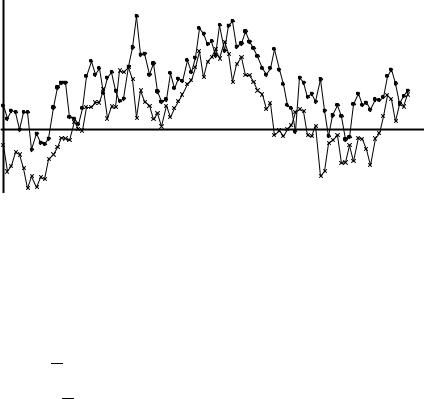
17.5. Коинтеграция. Регрессии с интегрированными переменными |
559 |
Рис. 17.2. Два коинтегрированных процесса при λ = 1 |
|
Если переменные в регрессии не стационарны, но действительно связаны друг с другом стационарной линейной комбинацией (модель специфицирована верно), то полученные оценки коэффициентов этой линейной комбинации будут на самом деле сверхсостоятельными, т.е. будут сходиться по вероятности к истинным коэффициентам√со скоростью, пропорциональной не квадратному корню количества наблюдений T , как в регрессии со стационарными переменными, а со скоростью,
пропорциональной просто количеству наблюдений T . Другими словами, в обыч-
√
ной регрессии T (λ −λ) имеет невырожденное асимптотическое распределение, где λ — полученная из регрессии оценка λ, а в регрессии с I(1)-переменными T (λ − λ) имеет невырожденное асимптотическое распределение.
Обычные асимптотические аргументы сохраняют свою силу, если речь идет об оценках параметров краткосрочной динамики в модели исправления ошибок. Таким образом, можно использовать t-статистики, получаемые обычным методом наименьших квадратов, для проверки гипотез о значимости отдельных переменных. Важно помнить, что это относится к оценкам краткосрочных параметров. Этот подход не годится для проверки гипотез о коэффициентах коинтеграционной комбинации.
Определение коинтеграции естественным образом распространяется на случай нескольких переменных произвольного порядка интегрирования. Компоненты k-мерного векторного процесса xt = (x1t, . . . , xkt) называют коинтегрированными порядка d и b, что обозначается xt CI(d, b), если
1)каждая компонента xit является I(d), i = 1, . . . , k;
2)существует отличный от нуля вектор β, такой что xtβ I(d − b), d b > 0. Вектор β называют коинтегрирующим вектором.

560 |
Интегрированные процессы... |
Коинтегрирующий вектор определен с точностью до множителя. В рассмотренном ранее примере коинтегрирующий вектор имеет вид β = (−1, λ). Его можно пронормировать: β = (−1/λ, 1), или так, чтобы сумма квадратов элементов была
1 |
|
|
λ |
|||
равна 1, т.е. β = − |
√ |
|
, |
√ |
|
. |
1 + λ2 |
1 + λ2 |
|||||
17.6.Оценивание коинтеграционной регрессии: подход Энгла—Грейнджера
Если бы коэффициент λ был известен, то выяснение того, коинтегрированы ли переменные x1t и x2t, было бы эквивалентно выяснению того, стационарна ли комбинация x1t − λx2t (например, с помощью критерия Дики—Фуллера). Но в практических ситуациях обычно стационарная линейная комбинация неизвестна. Значит, необходимо оценить коинтегрирующий вектор. После этого следует выяснить, действительно ли этот вектор дает стационарную линейную комбинацию.
Простейшим методом отыскания стационарной линейной комбинации является метод Энгла—Грейнджера. Энгл и Грейнджер предложили использовать оценки, полученные из обычной регрессии с помощью метода наименьших квадратов. Одна из переменных должна стоять в левой части регрессии, другая — в правой:
x1t = λx2t + εt.
Для того чтобы выяснить, стационарна ли полученная линейная комбинация, предлагается применить метод Дики—Фуллера к остаткам из коинтеграционной регрессии. Нулевая гипотеза состоит в том, что εt содержит единичный корень, т.е. x1t и x2t не коинтегрированы. Пусть et — остатки из этой регрессии. Проверка нулевой гипотезы об отсутствии коинтеграции в методе Энгла—Грейнджера проводится с помощью регрессии:
et = ϕet−1 + ut. |
(17.14) |
Статистика Энгла—Грейнджера представляет собой обычную t-статистику для проверки гипотезы ϕ = 1 в этой вспомогательной регрессии. Распределение статистики Энгла—Грейнджера будет отличаться (даже асимптотически), от распределения DF-статистики, но имеются соответствующие таблицы. Если мы отклоняем гипотезу об отсутствии коинтеграции, то это дает уверенность в том, что полученные результаты не являются ложной регрессией.
Игнорирование детерминированных компонент ведет к неверным выводам о коинтеграции. Чтобы этого избежать, в коинтеграционную регрессию следует добавить соответствующие переменные — константу, тренд, квадрат тренда, сезонные

562 |
Интегрированные процессы... |
же нестационарную компоненту, называемую общим трендом. Выше мы получили для интегрированной переменной разложение Бевериджа—Нельсона на детерминированный тренд, стохастический тренд и стационарную составляющую. Следует показать, что стохастические тренды в двух коинтегрированных переменных должны быть одними и теми же.
Проведем сначала подобный анализ для детерминированных трендов. Пусть процессы {xt} и {zt} стационарны относительно некоторого тренда f (t), не обязательно линейного:
xt = µ0 + µ1f (t) + εt и zt = ν0 + ν1f (t) + ξt,
где εt и ξt — два стационарных процесса. В каком случае линейная комбинация этих двух процессов будет стационарной в обычном смысле (не относительно тренда)? Найдем линейную комбинацию xt − λzt:
xt − λzt = µ0 − λν0 + (µ1 − λν1)f (t) + εt − λξt.
Для ее стационарности требуется, чтобы µ1 = λν1 .
С другой стороны, если бы {xt} содержал тренд f (t), а {zt} — отличный от него тренд g(t), то, в общем случае, не нашлось бы линейной комбинации, такой что µ1f (t) − λν1g(t) оказалась бы постоянной величиной. Следовательно, для {xt} и {zt} не нашлось бы коинтегрирующего вектора. Коинтегрирующий
вектор можно найти только в том случае, если f (t) = λν1 g(t) для некоторого λ,
µ1
т.е. если f (t) и g(t) линейно зависимы.
Пусть теперь {xt} и {zt} — два процесса I(1), для которых существуют разложения Бевериджа—Нельсона:
xt = γt + vt + εt, zt = δt + wt + ξt,
где vt и wt — случайные блуждания, а εt и ξt — стационарные процессы. Найдем условия, при которых линейная комбинация xt и zt ,
xt − λzt = γt + vt + εt − λ(δt + wt + ξt) = (γ − λδ)t + vt − λwt + εt − λξt,
может быть стационарной. Для стационарности требуется, чтобы в получившейся переменной отсутствовал как детерминированный, так и стохастический тренд. Это достигается при γ = λδ и vt = λwt . При этом xt можно записать как
xt = λ(δt + wt) + εt,
т.е. {xt} и {zt} содержат общий тренд δt + wt.
