ЭКОНОМЕТРИКА и математическая экономика / Эконометрика. Учебник продвинутый (2005)

αj

где p — степень многочлена, p < q. Вводя такую зависимость, мы накладываем q − p линейных ограничений на структуру лага.

Простейший полиномиальный лаг — линейный. Для него αj = γ0 + γ1j. Как правило, здесь γ1 < 0. Его структура изображена на диаграмме (рис. 15.1).

Поскольку исходная модель регрессии линейна и ограничения, которые полиномиальный лаг накладывает на ее коэффициенты, являются линейными, то полученная модель останется линейной. Рассмотрим, каким образом ее можно оценить.

C учетом выражений для αj , проведем преобразование исходной модели:

Получим новую модель линейной регрессии:

p

xt = µ + γsyts + εt

s=0

с преобразованными факторами

Оценив γs , можно вычислить веса αj , воспользовавшись формулой (15.2).

При оценивании модели с ограничениями на структуру лага нужно проверить, правильно ли наложены ограничения. С помощью соответствующей F -статистики можно сравнить ее с исходной, неограниченной моделью, поскольку она является ее частным случаем. Модель

q

xt = µ + γsyts + εt

s=0

αj

j

эквивалентна исходной модели с точностью до линейных преобразований, поэтому достаточно проверить гипотезу о том, что последние q − p коэффициентов (γp+1, . . . , γq ) равны нулю.

Часто принимают, что веса на концах полиномиальной лаговой структуры (15.2) равны нулю. Это требование накладывает на коэффициенты модели дополнительные ограничения. Можно, например, потребовать, чтобы αq = 0, то есть

p

γsqs = 0.

s=0

Учесть такие ограничения несколько сложнее, но в целом не требуется выходить за рамки обычной линейной регрессии.

Геометрический лаг

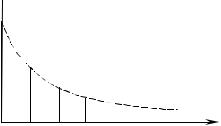
Еще один популярный вид структуры лага — геометрический лаг. Его веса αj задаются следующими соотношениями:

αj = α0δj , j = 0, . . . , ∞,

где 0 < δ < 1. Веса геометрического лага убывают экспоненциально с увеличением лага (рис. 15.2).

Модель распределенного лага с этими весами, модель Койка, имеет следующий вид:

j=0

Используя формулу суммы бесконечной геометрической прогрессии, получим

Чтобы избавиться от бесконечного ряда, к модели с геометрическим лагом применяют преобразование Койка (Koyck transformation). Сдвинем исходное уравнение на один период назад:

∞

xt−1 = µ + α0δj zt−j−1 + εt−1,

j=0

затем умножим это выражение на δ и вычтем из исходного уравнения (15.3):

Такой же результат можно получить, используя лаговые операторы:

Выражение в скобках упрощается с использованием формулы суммы бесконечной геометрической прогрессии:

1

xt = µ + α0 1 − δL zt + εt.

Умножим это уравнение на оператор (1 − δL):

(1 − δL) xt = (1 − δL) µ + α0zt + (1 − δL) εt

или учитывая, что оператор сдвига, стоящий перед константой, ее сохраняет, получаем формулу (15.4). В результате имеем следующую модель:

xt = µ + δxt−1 + α0zt + εt,

Как и в модели ARMA, такое преобразование корректно, если все корни многочлена ϕ(·) лежат за пределами единичной окружности.

Коэффициенты πi показывают влияние лагов переменной z на переменную x, то есть они представляют собой функцию реакции на импульс. Символически эти коэффициенты можно записать в виде:

πi = dxt . dzt−i

Рекуррентная формула для расчета коэффициентов πi получается дифференциацией по zt−i исходного уравнения модели (15.5):

для i < 0. В частном случае модели распределенного лага (когда p = 0) эта формула дает πi = αi , то есть влияние zt−i на πi количественно выражается коэффициентом при zt−i (весом лага).

Сумма коэффициентов πi показывает долгосрочное влияние z на x (долгосрочный мультипликатор). Она равна

По аналогии с моделью распределенного лага можно ввести показатель средней длины лага влияния z на x. Он равен

15.3.Модели частичного приспособления, адаптивных ожиданий и исправления ошибок

Рассмотрим некоторые прикладные динамические модели, сводящиеся к модели авторегрессионного распределенного лага.

Модель частичного приспособления

В экономике субъекты не сразу могут приспособиться к меняющимся условиям — это происходит постепенно. Нужно время на изменение запасов, обучение, переход на новые технологии, изменение условий долгосрочных контрактов и т.д. Эти процессы можно моделировать с помощью модели частичного приспособления.

Для иллюстрации приведем следующий пример: инфляция зависит от денежной массы, меняя денежную массу, мы можем получить какой-то желаемый уровень инфляции. Но реальность несколько запаздывает.

Пусть xDt — желаемый уровень величины xt, zt — независимый фактор, определяющий xDt . Тогда модель частичного приспособления задается следующими двумя уравнениями:

xDt = β + αzt + ξt, (15.7) xt − xt−1 = γ(xDt − xt−1) + εt.

510 Глава 15. Динамические модели регрессии

Здесь γ [0; 1] — скорость приспособления. Если γ = 0, то xt = xt−1 , то есть xt не меняется, если же γ = 1, то приспособление происходит мгновенно, и в этом случае сразу xt = xDt .

Предположим, что переменная xDt ненаблюдаема. Исключим из этих двух выражений ненаблюдаемую переменную:

xt = γβ + (1 − γ)xt−1 + γαzt + εt + γξt.

Ясно, что это модель ADL(1, 0), где γβ = µ, 1−γ = ϕ1 и γα = α0 . Оценив параметры µ, ϕ1 и α0 , мы можем с помощью обратного преобразования вычислить оценки параметров исходной модели.

Модель адаптивных ожиданий

Очень часто экономические решения, принимаемые людьми, зависят от прогнозов того, что будет в будущем. При этом уровень экономических величин, на которые воздействуют такие решения, зависит не от текущего значения показателя, а от ожидаемого значения (например, если ожидается высокий уровень инфляции, то следует скупать доллары, курс доллара в результате вырастет). В теории рассматриваются 2 вида ожиданий — рациональные и адаптивные. В соответствии с одним из определений, ожидания называют рациональными, если математическое ожидание прогноза равно фактическому значению, которое будет в будущем. Модели рациональных ожиданий часто оказываются довольно сложными. Адаптивные ожидания — это ожидания, которые зависят только от предыдущих значений величины. По мере того, как наблюдаются процессы движения реальной величины, мы адаптируем наши ожидания к тому, что наблюдаем на самом деле.

Чтобы ввести в экономические модели ожидания экономических субъектов, в простейшем случае используют модель адаптивных ожиданий. Адаптивные ожидания некоторой величины формируются только на основе прошлых значений этой величины. Например, пусть xt зависит от ожиданий ( ztE ) величины zt, zt — величина, от прогноза которой должен зависеть xt (например, инфляция), ztE — ожидание (прогноз) этой величины в момент времени t.

xt = β + αztE + εt.

В целом xt выгодно выбирать в зависимости от того, какой величина zt будет в будущем: zt+1 , zt+2, . . ., однако в момент выбора t известны только текущее и прошлые значения ( . . ., zt−1 , zt).

Ошибка в ожиданиях ztE приводит к их корректировке. Модель адаптации ожиданий к фактическому значению zt записывается так:

ztE − ztE−1 = θ(zt − ztE−1),

где θ — скорость приспособления ожиданий. Если θ = 0, то ожидания никак не адаптируются к действительности и прогнозы не сбываются (скорость адаптации нулевая); если θ = 1, скорость адаптации мгновенная, наши ожидания сбываются (полностью адаптировались): ztE = zt. Обычно 0 < θ < 1.

Легко видеть, что модель адаптации ожиданий основывается на формуле экспоненциальной средней:

ztE = θzt + (1 − θ)ztE−1.

Для оценки параметров модели надо исключить ненаблюдаемые ожидания ztE . Используя лаговый оператор, получаем:

ztE − (1 − θ)ztE−1 = (1 − (1 − θ)L)ztE = θzt,

Таким образом, ожидания в рассматриваемой модели описываются бесконечным геометрическим распределенным лагом с параметром затухания δ = 1 − θ.

Если в уравнение для xt вместо ztE подставить данный бесконечный ряд, то получится модель регрессии с геометрическим распределенным лагом:

Как было показано ранее, модель геометрического лага с помощью преобразования Койка приводится к модели ADL. Умножим обе части уравнения 15.8 на 1 − (1 − θ)L и получим:

(1 − (1 − θ)L)xt = (1 − (1 − θ)L)β + αθzt + (1 − (1 − θ)L)εt.

После соответствующего переобозначения параметров модель адаптивных ожиданий приобретает новую форму — ADL(1, 0) с MA(1)-ошибкой:

xt = θβ + (1 − θ)xt−1 + αθzt + εt − (1 − θ)εt−1.

Оценивать модель адаптивных ожиданий можно теми же методами, что и модель Койка.

Модель исправления ошибок

Вдинамических регрессионных моделях важно различие между долгосрочной

икраткосрочной динамикой. Это различие можно анализировать в рамках модели исправления ошибок. Рассмотрим в долгосрочном аспекте модель ADL(1, 1):

xt = µ + ϕ1xt−1 + α0zt + α1zt−1 + εt.

Предположим, что фактор zt и ошибка εt являются стационарными процессами. Тогда при |ϕ1| < 1 изучаемая переменная xt также стационарна. Возьмем математические ожидания от обеих частей уравнения модели:

x¯ = µ + ϕ1x¯ + α0z¯ + α1z¯.

В этой формуле x¯ = E(xt), z¯ = E(zt) (стационарные уровни x и z) и учитывается, что E(εt) = 0. Получаем уравнение

которое описывает долгосрочное стационарное состояние экономического процесса. Коэффициент

отражает долгосрочное влияние z на x. Он совпадает с долгосрочным мультипликатором (15.6).

Модель ADL(1, 1) можно привести к виду, который описывает краткосрочную динамику экономической системы. В этом виде модель называется моделью исправления ошибок, сокращенно ECM (error-correction model):

где θ = 1 − ϕ1 , ∆xt = xt − xt−1 , ∆zt = zt − zt−1 .

Предполагается, что если в предыдущий период переменная x отклонилась от своего «долгосрочного значения» µ +λz, то элемент xt−1 −(µ +λzt−1) корректирует динамику в нужном направлении. Для того чтобы это происходило, необходимо выполнение условия |ϕ1| < 1.