ЭКОНОМЕТРИКА и математическая экономика / Эконометрика. Учебник продвинутый (2005)

12.Утверждается, что «модель GARCH более компактна, чем модель ARCH». Что при этом имеется в виду? Почему важна «компактность» модели?

13.Докажите, что процесс GARCH(p, q) не автокоррелирован.

14.Докажите, что процесс GARCH(p, q) является белым шумом, если существует его безусловная дисперсия.

15.Пользуясь представлением квадратов процесса GARCH(1, 1) в виде ARMA(1, 1) выведите их автокорреляционную функцию.

16.Запишите автокорреляционную функцию квадратов процесса GARCH(1, 1). Покажите, что при значении суммы коэффициентов δ1 + γ1 , приближающемся к 1 (но меньшем 1) автокорреляционная функция затухает медленно. Покажите, что при фиксированном значении суммы коэффициен-

тов δ1 + γ1 = ϕ (0 < ϕ < 1), автокорреляция тем слабее, чем меньше γ1 , и стремится к нулю при γ1 → 0.

17.Рассмотрите следующую модель с авторегрессионной условной гетероскедастичностью:

где f (z) = |z| − ϕz.

а) Укажите значения параметров, при которых эта модель сводится к обычной модели GARCH.

б) Утверждается, что в этой модели имеет место асимметричность влияния «шоков» εt на условную дисперсию. Что при этом имеется в виду? При каких значениях параметров влияние будет симметричным?

18.Запишите модель GARCH(1, 1)-M с квадратным корнем условной дисперсии в уравнении регрессии (с расшифровкой обозначений).

19.Рассмотрите модель AR(1) с независимыми одинаково распределенными ошибками и модель AR(1) с ошибками, подчиняющимися процессу GARCH.

а) Объясните, почему точечные прогнозы по этим двум моделям не будут отличаться.

б) Как будут отличаться интервальные прогнозы?

20.Пусть имеется некоторый процесс с авторегрессионной условной гетероскедастичностью εt , задаваемый моделью

σ2 = var(εt|Ωt−1) = h(σ2−1, . . . , σ2− , ε2−1, . . . , ε2− ),

t t t p t t q

где Ωt−1 — предыстория процесса, h(·) — некоторая функция и εt = ξtσt. Предполагается, что инновации ξt имеют стандартное нормальное распределение и не зависят от предыстории Ωt−1 . Найдите куртозис εt, если известно, что E(σt2) = 5, E(σt4) = 100. О чем говорит величина куртозиса?

21.Докажите, что эксцесс распределения отдельного наблюдения εt процесса

ARCH(1)

εt = ξtσt, σ2 = ω + γε2−1, ξt N ID(0, 1)

t t

6γ2

равен 1 − 3γ2 .

22.Какие сложности возникают при построении прогнозных интервалов процесса GARCH с заданным уровнем доверия (например, 95%)? Каким способом можно обойти эту проблему?

23.Почему модель GARCH не подходит для прогнозирования автокоррелированных временных рядов?

Рекомендуемая литература

1.Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика — начальный курс. — М.: «Дело», 2000. (Гл. 12).

2.Предтеченский А.Г. Построение моделей авторегрессионной условной гетероскедастичности (ARCH) некоторых индикаторов российского финансового рынка (дипломная работа), ЭФ НГУ, 2000.

( ).

3.Шепард Н. Статистические аспекты моделей типа ARCH и стохастическая волатильность. Обозрение прикладной и промышленной математики. Т. 3, вып. 6. — 1996.

4.Baillie Richard T. and Tim Bollerslev. Prediction in Dynamic Models with Time Dependent Conditional Variances // Journal of Econometrics, No. 52, 1992.

5.Bera A.K. and Higgins M.L. ARCH Models: Properties, Estimation and Testing // Journal of Economic Surveys, No. 7, 1993.

6.Bollerslev T., Engle R.F. and Nelson D.B. ARCH Models // Handbook of Econometrics. Vol. IV. Ch. 49. — Elsevier Science, 1994.

7.Bollerslev Tim. Generalized Autoregressive Conditional Heteroskedasticity // Journal of Econometrics, No. 31, 1993.

8.Bollerslev Tim, Ray Y. Chou and Kenneth F. Kroner. ARCH Modeling in Finance: A Review of the Theory and Empirical Evidence // Journal of Econometrics, No. 52, 1992.

9.Campbell John Y., Lo Andrew W., MacKinlay A. Craig. The Econometrics of Financial Markets. — Princeton University Press, 1997. (Ch. 12).

10.Diebold, Francis X. and Jose A. Lopez Modeling Volatility Dynamics, Macroeconometrics: Developments, Tensions and Prospects. — Kluwer Academic Press, 1995.

11.Engle, Robert F. Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K. Inflation // Econometrica, No. 50, 1982.

12.Greene W.H. Econometric Analysis. — Prentice-Hall, 2000. (Ch. 18).

13.Hamilton James D. Time Series Analysis. Ch. 21. — Princeton University Press, 1994.

14.Mills Terence C. The Econometric Financial Modelling Time Series. — Cambridge University Press, 1999. (Ch. 4).

Глава 17

Интегрированные процессы, ложная регрессия

икоинтеграция

17.1.Стационарность и интегрированные процессы

Для иллюстрации различия между стационарными и нестационарными случайными процессами рассмотрим марковский процесс, т.е. авторегрессию первого порядка:

xt = µ + ϕxt−1 + εt,

или

(1 − ϕL)xt = µ + εt.

В данной модели xt — не центрированы.

Будем предполагать, что ошибки εt — независимые одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией σε2 . Как известно, при |ϕ| < 1 процесс авторегрессии первого порядка слабо стационарен и его можно представить в виде бесконечного скользящего среднего:

Условие |ϕ| < 1 гарантирует, что коэффициенты ряда затухают. Математиче-

µ

ское ожидание переменной xt постоянно: E(xt) = 1 − ϕ . Дисперсия равна

Найдем также автоковариации процесса:

Таким образом, рассматриваемый процесс слабо стационарен, поскольку слабое определение стационарности требует, чтобы математическое ожидание xt было постоянным, а ковариации не зависели от времени, но только от лага. На самом деле, поскольку ошибки εt одинаково распределены, то он стационарен и в строгом смысле.

При |ϕ| > 1 это будет взрывной процесс. Такие процессы рассматриваться не будут.

Как известно (см. гл. 14), авторегрессионный процесс первого порядка при ϕ = 1 называют случайным блужданием. Если µ = 0, то это просто случайное блуждание, а при µ = 0 это случайное блуждание с дрейфом.

У процесса случайного блуждания, начавшегося бесконечно давно, не существует безусловного математического ожидания и дисперсии. За бесконечное время процесс «уходит в бесконечность», его дисперсия становится бесконечной. В связи с этим будем рассматривать все моменты процесса случайного блуждания как условные, т.е. будем действовать так, как если бы x0 была детерминированной величиной. Выразим xt через x0 :

t

xt = x0 + µt + εi.

i=1

Таким образом, константа (дрейф) в авторегрессионной записи процесса приводит к появлению линейного тренда в xt. Мы получили разложение процесса xt на две составляющие: детерминированный линейный тренд µt и случайное блуж-

εt = ∆εt . Вторую составляющую, как мы помним, называют стохастическим трендом, поскольку влияние каждой ошибки не исчезает со временем.

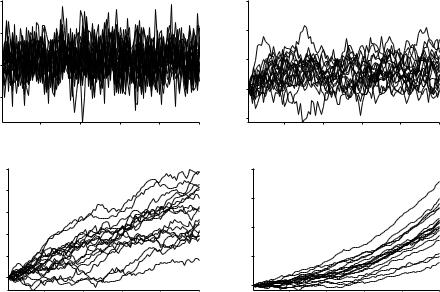
Рис. 17.1. Поведение процесса AR(1) в зависимости от значения ϕ

Используя данное представление, найдем математическое ожидание и дисперсию:

E(xt|x0) = x0 + µt.

tt

Дисперсия со временем растет линейно до бесконечности.

Случайное блуждание является примером авторегрессионого процесса с единичным корнем. Это название следует из того, что при ϕ = 1 корень характеристического многочлена 1 −ϕL, соответствующего процессу AR(1), равен единице.

Рисунок 17.1 иллюстрирует поведение марковских процессов при различных коэффициентах авторегрессии. На каждом из графиков изображены 20 рядов длиной T = 100, случайно сгенерированных по формуле xt = 0.3 + ϕxt−1 + εt с разными значениями ϕ: 1) ϕ = 0.1; 2) ϕ = 0.9; 3) ϕ = 1; 4) ϕ = 1.02. Во всех случаях использовалось стандартное нормальное распределение для εt и x0 = 0.

Добавим к стационарному процессу AR(1) детерминированный тренд µ1t:

xt = µ0 + µ1t + ϕxt−1 + εt.

Можно также записать уравнение процесса в виде:

(xt − γ0 − γ1t) = ϕ(xt−1 − γ0 − γ1(t − 1)) + εt.

Ясно, что если вычесть из xt тренд γ1t, то получится стационарный процесс. Подобного рода процессы называют стационарными относительно тренда.

Рассмотрим теперь процесс ARMA(p, q):

p q

xt = ϕixt−i + εt − θiεt−i. i=1 i=1

Если все корни характеристического многочлена

p

ϕ(z) = 1 − ϕizi

i=1

по абсолютной величине больше 1, т.е. лежат за пределами единичного круга на комплексной плоскости, то процесс стационарен. Если один из корней лежит в пределах единичного круга, то процесс взрывной. Если же d корней равны единице, а остальные лежат за пределами единичной окружности, то процесс нестационарный, но не взрывной и о нем говорят, что он имеет d единичных корней.

Нестационарный процесс, первые разности которого стационарны, называют интегрированным первого порядка и обозначают I(1). Стационарный процесс обозначают I(0). Если d-e разности случайного процесса стационарны, то его называют интегрированным d-го порядка и обозначают I(d).

Рассмотрим, например, процесс

t

yt = xi, где xt = xt−1 + εt.

i=1

Он будет I(2), то есть его вторые разности, ∆2yt, стационарны.

Для процессов ARIMA можно дать более удачное определение интегрированности. Процессом I(0) называется стационарный процесс с обратимым скользящим средним. Процесс I(d) — такой процесс, d-e разности которого являются I(0). Соответственно, процесс, являющийся d-ой разностью процесса I(0), будет I(−d). Такое уточнение нужно для того, чтобы необратимые процессы, такие как εt −εt−1 , где εt — белый шум, по определению были I(−1), но не I(0). По этому уточненному определению процесс I(d) при d > 0 будет иметь в точности d единичных корней.

17.2.Разложение Бевериджа—Нельсона для процесса I(1)

Рассмотрим ARIMA-процесс I(1), интегрированный первого порядка. Пусть его исходная форма, записанная через лаговый оператор, имеет вид

ϕ(L)xt = µ + θ(L)εt.

Поскольку это процесс I(1), то многочлен ϕ(L) имеет единичный корень и уравнение процесса можно представить в виде

(1 − L)ϕ (L)xt = ϕ (L)∆xt = µ + θ(L)εt,

где у многочлена ϕ (L) все корни находятся за пределами единичного круга. Отсюда следует разложение Вольда для приростов ∆xt, которые являются стационарными:

Таким образом, можно представить ∆xt в виде

∆xt = γ + (c(1) + c (L)(1 − L)) εt = γ + c(1)εt + c (L)∆εt.

Суммируя ∆xt, получим

xt = γt + c(1)εt + c (L)εt,

где εt — случайное блуждание, такое что ∆εt = εt . Без доказательства отметим,

∞

что ряд c (L) сходится абсолютно1: |ci | < ∞. Следовательно, он соответствует

i=0

разложению Вольда стационарного процесса.

Мы получили так называемое разложение Бевериджа—Нельсона. Процесс xt вида I(1) мы представили как комбинацию детерминированного тренда γt, стохастического тренда c(1)εt и стационарного процесса c (L)εt , который здесь обычно интерпретируется как циклическая компонента.

17.3. Ложная регрессия

Одним из важнейших условий получения корректных оценок в регрессионных моделях является требование стационарности переменных. В экономике довольно часто встречаются стационарные ряды, например, уровень безработицы. Однако, как правило, экономические процессы описываются нестационарными рядами: объем производства, уровень цен и т.д.

эффициенты ci у стационарного процесса ARMA сходятся экспоненциально, то ряд должен сойтись (экспоненциальное убывание превосходит рост i).