
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание
x1 x2 x2 x3 x4 x1 x2 x3 x1 x3 x4 x2 x1 x3 x2 − сокращенная д. н.
ф., x1 x2 −ядровая д. н. ф. 5. а) 2n−1 ; б) 2n−1 .
§1.7. Схемы из функциональных элементов
Каждой бинарной операции в алгебре логики соответствует функциональный элемент с двумя
FF входами и одним выходом, унарной – с одним входом и одним выходом (см. рис. 1.7). Если набор функциональных элементов (ФЭ)
а) |
б) |
соответствует полной системе в P2 , то любую |
|
Рис. 1.7 |
булеву функцию можно выразить формулой через |
|
функции полной системы и реализовать ее с |
|
|
|
помощью соответствующих ФЭ. |
Определение. Логическая схема Σ(x1 , K, xn ) , выходные сигналы zq
которой описываются системой булевых функций zq = fq (x1 , K, xn ) ,
где xi − входные сигналы логической схемы (1 ≤ i ≤ n , 1 ≤ q ≤ k )
называется схемой функциональных элементов (СФЭ).
Теорема. Для того, чтобы для произвольной системы
z1 = f1 (x1 , K, xn ),
KKKKK
zk = fk (x1 , K, xn )
существовала схема Σ(x1 , K, xn ) из ФЭ с n входами x1 , K, xn и k выходами z1 , K, zk необходимо и достаточно, чтобы набор ФЭ
соответствовал полной системе функций.
Обычно для построения схем используются базис { , &, ¬} (этот базис называется стандартным или булевым) или { , &} (базис Жегалкина).
Определение. Обозначим через L(Σ) функционал, равный числу
элементов в схеме Σ, означающий сложность схемы.
Проблема синтеза – построить схему с минимальной сложностью.
Решение типовых примеров
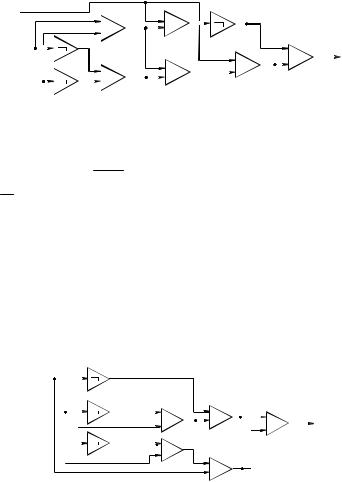
1. Представить формулой функцию, заданную схемой
x |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|||||||
|
|
|
& |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
||||||||
z |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
& |
|
|
|
|
d |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
b |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Рис. 1.8 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Имеем: a = yz, |
b = y z, c = |
|
|
|
, |
|
|
d = x(a b), |
|
||||||||||||
x a |
|
|
|
||||||||||||||||||
f = c d. Отсюда
f (x, y, z) = c d = x a x(a b) = x a x(a b) =
= x yz x( yz y z) = x( y z) xyz x y z =
= x y x z xyz x y z = y(x xz) x z xyz =
=y(x z) x z xyz = x y y z x z xyz.
2.Построить схему, реализующую функцию
f (x, y, z) = x( y z) xyz.
Решение. Положим a = y z, b = xa, |
c = x y z. |
Схема, реализующая |
|||||||||||
функцию, выглядит так: |
|
|
|
|
|
|
|||||||
|
|
x |
|
|
|
|
|
|
|
||||
y |
|
& |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
b |
|
||||
z |
|
|
|
|
a |
|
|
||||||
|
|
||||||||||||
|
|
|
|
|
& |
|
& |
c |
|
|
|
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.9 |
|
|
|
|
|
|
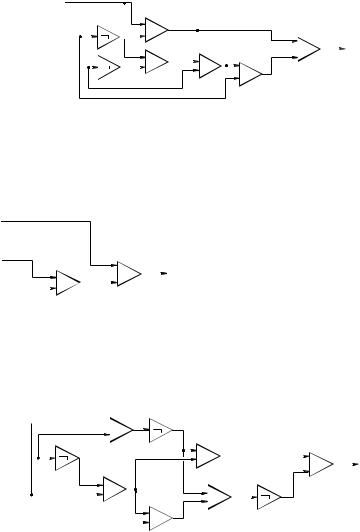
3. Упростить схему (рис. 1.10). |
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
y |
|
& |
a |
|
|
|
f |
||||
|
|
|
|
|
|
b |
|
|
|||
z |
|
|
|
& |
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
& |
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Рис. 1.10 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Решение. Требуется построить схему с меньшим числом функциональных элементов, реализующую ту же функцию f (x, y, z).
Для этого выразим f |
формулой и упростим формулу. Имеем: |
|||||||
f = a by = x y (xz z) y = x y (x z) y = x y xy yz = |
||||||||
x |
|
|
|
|
|
|
= x( y y) yz = x yz. |
|
y |
|
|
|
|
|
|
Следовательно, функция f |
|
|
|
|
|
|
|
может быть реализована схемой |
||
z |
|
|
|
|
|
f |
из 2 функциональных элементов |
|
& |
|
|
(рис. 1.11). |
|||||
|
|
|
|
|||||
|
|
|
Рис. 1.11 |
|
|
|
|
|
Задачи для самостоятельного решения
1. Представить формулой функцию, заданную схемой (рис. 1.12).
 &
&
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
f |
||||
|
|
|
|
|
|
|
|
|
|
|||||
y |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Рис. 1.12 |
|
|
|
|
|
|||
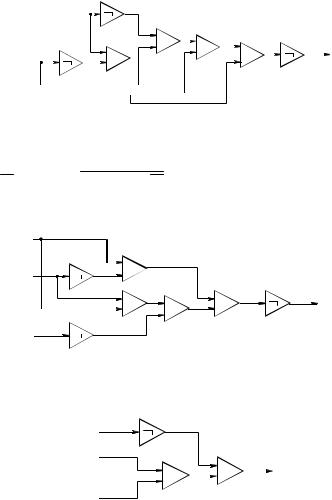
2. Представить схемой функцию |
f = |
x y x yz |
. |
|
|
|
|
|
|||||||||
3. Упростить схему (рис. 1.13). |
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
& |
|
& |
|
|
|
|
|
|
f |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 1.13
Ответы
1. f = xy (x y) x y z xy (выражение не упрощено). 2. Схема изображена на рис. 1.14.
x
y
z
& |
|
|
|
& |
& |
|
f |
Рис. 1.14
3. Схема изображена на рис. 1.15.
x y
z
& |
|
|
|
f |
|
||||
|
|
|||
Рис. 1.15 |
|
|
|
|
§1.8. Функции k -значной логики
Рассмотрим множество Ek ={0,1, K, k −1} .
Определение. Функция f : Ekn → Ek называется функцией k -значной логики от n переменных.
Для задания функции f (x1 , K, xn ) достаточно указать ее значения на каждом наборе переменных из Ekn .
|
|
|
|
|
Табл. 1.12 |
|
|
|
|
|
|
x1 |
x2 |
K |
xn−1 |
xn |
f (x1 , K, xn ) |
0 |
0 |
K |
0 |
0 |
f (0, 0, K, 0, 0) |
0 |
0 |
K |
0 |
1 |
f (0, 0, K, 0,1) |
K |
K |
K |
K |
K |
K |
|
|
|
|
|
|
0 |
0 |
K |
0 |
k −1 |
f (0, 0, K, 0, k −1) |
0 |
0 |
K |
1 |
0 |
f (0, 0, K,1, 0) |
K |
K |
K |
K |
K |
K |
|
|
|
|
|
|
0 |
0 |
K |
k −1 |
k −1 |
f (0, 0, K, k −1, k −1) |
K |
K |
K |
K |
K |
K |
|
|
|
|
|
|
k −1 |
k −1 |
K |
k −1 |
k −1 |
f (k −1, k −1, K, k −1, k −1) |
Имея ввиду стандартное расположение наборов (в соответствии с увеличением их номера), наборы представляют собой разложения в k -
ичной системе счисления чисел 0,1, K, k n −1.
Обозначим Pk (n) − множество всех функций k -значной логики от n - переменных, а Pk − множество всех функций k -значной логики.
Аналогично тому, как поступали при подсчете числа булевых функций, зависящих от n переменных, можно доказать следующую теорему.
Теорема. | Pk (n) | = k k n .
Замечание. Видно, что в отличие от булевой алгебры в Pk при k ≥ 3 существенно возрастают сложности в эффективном использовании

табличного задания функций. Так, уже в простейшем случае
| P3 (2) |= 332 = 39 =19683 .
В Pk часто используют вместо табличного задания функций задание при помощи алгоритма вычислимости функций. Например,
max(x1 ,K, xn ) .
Вводя (по аналогии с P2 ) понятие существенной и фиктивной
переменной, а также понятие равенства функций, можно рассматривать все функции с точностью до фиктивной переменной.
Рассмотрим примеры некоторых считаемых элементарными функций
Pk .
1)0,1, K, k −1 – константы.
2)x = x +1 (mod k) , где x представляет собой обобщение отрицания в
смысле “циклического” сдвига значений, – отрицание Поста.
3) Nx = k −1 − x , где Nx (часто обозначают ~ x ) представляет собой обобщение отрицания в смысле “зеркального” отображения значений, –
отрицание Лукашевича.
4) |
1 при x = i, |
(0 |
≤ i ≤ k −1) – характеристическая |
||
ji (x) = |
|
||||
|
0 при x ≠ i |
|
|
|
|
функция (первого рода) числа i . |
|
||||
5) |
k −1 при x = i, |
(0 ≤ i |
≤ k −1) – характеристическая |
||
Ji (x) = |
0 при x ≠ i |
||||
|
|
|
|
||
функция (второго рода) числа i . |
|
||||
6) |
min(x1 , x2 ) – обобщение конъюнкции (другие обозначения x1x2 , |
||||
x1 & x2 , x1 x2 ) – минимум x1 и |
x2 . |
||||
7)x1 x2 (mod k) – другое обобщение конъюнкции – произведение x1
и x2 по модулю k .
8)max(x1 , x2 ) – обобщение дизъюнкции (другое обозначение
x1 x2 ) – максимум x1 и x2 .
9) x1 + x2 (mod k) – сумма x1 и x2 по модулю k .
|
x1 −& |
x2 |
0, если x1 < x2 , |
|
|
|
|
|
|
|
||||||||
10) |
= x |
− x |
2 |
, если x |
2 |
≤ x |
|
– усеченная разность. |
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|||
11) |
max(x1 , x2 ) +1(mod k) = |
|
|
|
|
|
|
|
|
|||||||||
= x |
|
− x |
|
= |
x1 − x2 , если x2 ≤ x1 , |
< x |
– разность x и x |
|
по |
|||||||||
1 |
|
2 |
|
k − |
(x |
2 |
− x ), если x |
1 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
2 |
|
|
|
модулю k (функция Вебба). |
|
|
|
|
|
|
|
|
|
|||||||||
12) |
x1 x2 |
k |
−1, |
если x |
< x |
2 |
, |
|
– импликация. |
|
||||||||
= |
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
(k −1) − x1 + x2 , если x2 ≤ x1 |
|
|
|||||||||||
Следующие равенства вводятся по определению.
Определение.
max(x1 , x2 , K, xn−1 , xn ) = max(max(x1 , x2 , K, xn−1 ), xn ), n ≥ 3;
min(x1 , x2 , K, xn−1 , xn ) = min(min( x1 , x2 , K, xn−1 ), xn ), n ≥ 3;
0, если x = 0,
− x =
k − x, если x ≠ 0.
По аналогии с булевой алгеброй в k -значной логике:
–вводится понятие формулы над множеством функций Φ ;
–каждой формуле U (x1 ,K, xn ) ставится в соответствие функция f (x1 ,K, xn ) и говорится, что формула U реализует функцию f ;
–формулы U и V считаются эквивалентными, если соответствующие им функции fU и fV равны.
Обратим внимание на то, что
1.в k -значной логике сохраняются многие свойства и результаты, которые имеют место в двузначной логике;
2.в k -значной логике при k ≥ 3 имеются принципиальные
отличия от алгебры логики. Так, имеют место равенства: 1. Коммутативность

x1 o x2 = x2 o x1 , где o {min, max, +, }. 2. Ассоциативность
(x1 o x2 ) o x3 = x1 o(x2 o x3 ) , где o {min, max, +, }. 3. Дистрибутивность умножения относительно сложения
(x1 + x2 ) x3 = (x1 x3 ) + (x2 x3 ) .
4.Дистрибутивность операции max относительно операции
min
max(min(x1 , x2 ), x3 ) = min(max(x1 , x3 ), max (x2 , x3 )) .
5.Дистрибутивность операции min относительно операции max
min(max(x1 , x2 ), x3 ) = max(min(x1 , x3 ), min (x2 , x3 )) .
6. Идемпотентность операций max и min max(x, x) = x, min(x, x) = x .
7. Аналоги правил де Моргана в P2
max(~ x1 , ~ x2 ) =~ min(x1 , x2 ), min(~ x1 , ~ x2 ) =~ max(x1 , x2 ) .
Следующее важное тождество, доказываемое непосредственной проверкой, представляет собой аналог СДНФ
f (x1 , K, xn ) = |
|
Jσ1 (x1 ) & K& Jσn (xn ) & f (σ1 , K, σ n ) . |
|
(σ1, K, σn ) |
|
Приведем примеры отличия k -значной логики (при k ≥ 3 ) от |
||
двузначной: |
|
|
1. При k ≥ 3 |
|
|
x |
≠ x , но ~ (~ x) = x при всех k ; |
|
2. min(x1 , x2 ) ≠ max(x1 , x2 ) , но ~ min(x1 , x2 ) = max(~ x1 , ~ x3 )
Определение. Класс функций Ψ ={ f1 , K, fm , K} из Pk называется
функционально полным, если любая функция из Pk |
может быть |
представлена в виде формулы над Ψ . |
|
Пример. Система Ψ = Pk − полная. |
|
Теорема. Система функций |
|
Ψ ={0, 1, K, J 0 (x), K, J k −1 (x), min(x1 , x2 ), |
max(x1 , x2 )} |
является полной в Pk . |
|
Доказательство. Пусть f (x1 , K, xn ) – произвольная функция Pk . Для нее имеет место разложение
f (x1 , K, xn ) = Jσ1 (x1 ) & K& Jσn (xn ) & f (σ1 , K, σn ).
(σ1, K, σn )
Данная формула (правая часть) построена из функций, входящих в систему Ψ . Такое представление функции f (x1 , K, xn ) называется
первой формой.
Для функций из Pk справедливо еще одно представление, называемое
второй формой
f (x1 , K, xn ) = ∑ f (σ1 , K, σ n ) jσ1 (x1 ) K jσn (xn ) .
(σ1, K, σn )
Если k = p − простое число, то, как и в случае двузначной логики,
каждая функция представима, и притом единственным образом, в виде полинома Жегалкина
f (x , ... , x ) = ∑Aσ σ xσ1 ... xσn ,
1 n σ1,...,σn 1 ... n 1 n
где Aσ1 ...σn E p−1 = {0,1,..., p −1}, а операции сложения и умножения производятся по модулю p; символ xσ понимается в обычном смысле: x0 =1, xσ = xσ −1 σ.
Наконец, если k = pn , где p − простое число, то можно установить взаимно однозначное соответствие между множеством
Ek |
={0,1,..., k −1} = {0,1,..., pn −1} и полем F = GF( pn ) (из |
pn |
элементов). Отождествим соответствующие элементы множеств |
Ek |
и F, т.е. будем считать, что на множестве Ek ={0,1,..., pn −1} |
заданы операции сложения и умножения, превращающие это множество в поле из pn элементов (эти операции не следует путать со сложением и умножением по модулю pn , ведь кольцо Z pn не является полем).
Теперь мы можем представлять функции в виде полиномов Жегалкина
f (x1 |
,..., xm ) = ∑Aα |
...α |
m |
xα1 |
... xαmm , |
|
1 |
|
1 |
|
|
|
α1 ...αm |
|
|
|
|
где α1, ... ,αm , Aα1...αm {0,1,..., pn −1}, а операции такие, как в
поле GF( pn ).
Пример. Представим функцию 3-значной логики
0, если x ≤ y, f (x, y) =
x, если x > y
в СДНФ и в виде полинома Жегалкина. Решение. Составим таблицу значений функции:
|
|
Табл. 1.13 |
|
|
|
|
|
x |
y |
|
f |
0 |
0 |
|
0 |
0 |
1 |
|
0 |
0 |
2 |
|
0 |
1 |
0 |
|
1 |
1 |
1 |
|
0 |
1 |
2 |
|
0 |
2 |
0 |
|
2 |
2 |
1 |
|
2 |
2 |
2 |
|
0 |
Рассматривая только те строки таблицы, где f = 0, получаем:
f(x, y) =
=(J1 (x) J 0 ( y) 1) (J 2 (x) J 0 ( y) 2) (J 2 (x) J 2 ( y) 2)=
=(J1 (x) J 0 ( y) 1) (J 2 (x) J 0 ( y)) (J 2 (x) J 2 ( y)).
|
|
|
|
|
|
|
|
2 |
|
|
Полином Жегалкина имеет вид |
f (x, y) = ∑aij xi y j . Запишем это |
|||||||||
|
|
|
|
|
|
|
|
i, j=0 |
|
|
выражение в матричной форме: |
|
|
|
|
|
|
|
|||
a |
00 |
a |
01 |
a |
02 |
1 |
|
|
1 |
|
|
|
|
|
|
= (1 |
|
|
|||
f = (1 x x2 ) a10 a11 |
a12 |
y |
|
x x2 )A y |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
|
|
|
2 |
|
|
2 |
||
a20 |
a22 y |
|
|
y |
|
|||||
Подставляя значения x, y {0,1, 2} и используя таблицу, получим:
