
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание
Задачи для самостоятельного решения
1. Автомат задан таблицей 3.5. Найти: а) ϕ(q2 , 0120), б) ψ(q3 ,1120).
|
|
|
|
Табл. 3.5 |
|
|
|
|
|
0 |
|
1 |
2 |
|
a,a |
|
|
|
|
|
b,a |
|
||||
q1 |
q2 |
a |
q3 |
q2 |
q1 |
q2 |
||
|
|
b |
a |
|
b,a |
|
||
q2 |
q1 |
|
q2 b |
q3 a |
|
a,b |
||
b |
a,a |
q3 |
||||||
|
||||||||
q3 |
q1 |
a |
q2 |
q2 |
|
|
b,b |
|
|
|
a |
b |
|
|
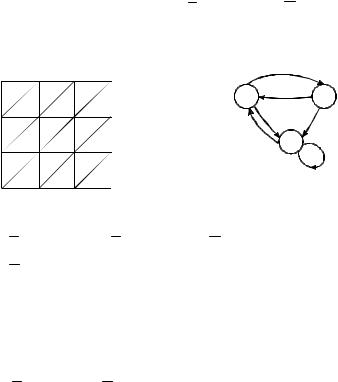
Рис. 3.13 2. Автомат задан диаграммой Мура, изображенной на рис. 3.13. Найти: а) ϕ(q3 ,baab), б) ϕ(q3 , a200 ), в) ψ(q2 , abab),
г) ψ(q2 ,b10 ).
3. Автомат задан каноническими уравнениями
q(t +1) = q(t) + a(t) +1,b(t) = q(t) + 2a(t),
где Q = A = B ={0, 1, 2} и вычисления производятся по модулю 3.
Найти: а) ϕ(0,1220), б) ψ(1,1021).
Ответы:
1. а) q1; б) abaa. 2. а) q1; б) q2 ; в) bbaa; г) a2b8. 3. а) 2; б)
0020.
§3.4. Приведённый автомат

Назовём состояния q и q′ автомата V = ( A,Q, B,ϕ,ψ)
неотличимыми, если ψ(q, w) =ψ(q′, w) для всех w A+.
Состояния q и q′ отличимы, если ψ(q, w) ≠ψ(q′, w) при
некотором w A+. Положим q ~ q′, если q и q′ неотличичимы. Нетрудно видеть, что отношение неотличимости ~ на множестве Q состояний автомата V является отношением эквивалентности. Это отношение вызывает разбиение множества Q на непересекающиеся классы эквивалентности: Q = Q1 Q2 ... Qk . При этом любые
два состояния q, q′, лежащие в одном классе, неотличимы, а любые два состояния из разных классов отличимы.
Множество классов отношения ~ (фактор-множество Q / ~) обозначим
€ |
€ |
|
через Q. Построим новый автомат V. В качестве входного и |
||
|
€ |
A и B, |
выходного алфавитов автомата V возьмём те же множества |
||
которые были у автомата V , а в качестве множества состояний возьмём |
||
€ |
€ |
€ |
множество Q. |
Надо определить теперь функции ϕ€: Q × A |
→ Q и |
€ |
|
|
ψ€ : Q × A → B. |
|
|
€ |
a A. Наиболее естественным является следующее |
|
Пусть q€ Q, |
||
определение значения ϕ€(q€, a) : взять какой-нибудь элемент q, принадлежащий классу q€, найти ϕ(q, a), а затем класс, в котором лежит элемент ϕ(q, a), объявить значением ϕ€(q€, a). То есть считать, что
^ |
^ |
^ |
|
ϕ |
(q, a) =ϕ(q, a) |
(1) |
|
Докажем корректность этого определения, т.е. независимость от выбора представителя в классе эквивалентности. Пусть Определение будет некорректным, если окажется, что
Докажем, что определение корректно. Если
ϕ(q, a) ~/ ϕ |
′ |
|
|
|
|
|
|
′ |
|
|
|
||
(q , a), то ψ(ϕ(q, a), w) ≠ψ(ϕ(q , a), w) при |
|||||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
′ |
некотором w A |
. Это означает, что ψ(q, aw) |
|
|||||||||||
|
≠ψ(q , aw). |
||||||||||||
Следовательно, q ~/ q′, что противоречит условию. Итак, |
|||||||||||||
q ~ q |
′ |
ϕ |
|
|
|
|
′ |
|
|
|
|||
|
(q, a) ~ ϕ(q , a), поэтому определение (1) корректно. |
||||||||||||
Функцию ψ€ |
|
|
|
|
€ |
|
|
|
|||||
определим на Q по формуле |
|
|
|
||||||||||
|
|
|
|
|
|
|
ψ€(q€, a) =ψ(q, a). |
(2) |
|||||
По определению неотличимости состояний мы имеем |
|||||||||||||
q ~ q |
′ |
|
|
|
|
|
′ |
|
|
|
|||
|
ψ(q, a) ~ ψ(q , a), поэтому определение (2) корректно. |
||||||||||||
|
|
€ |
|
€ |
|
|
|
||||||
Автомат V = ( A,Q, B,ϕ€,ψ€) называется приведённым автоматом,
соответствующим автомату V = ( A,Q, B,ϕ,ψ).
Докажем, что у приведённого автомата все состояния отличимы
|
|
|
|
|
|
|
|
|
|
|
|
||
друг от друга. Пусть q€ ~ q′. Тогда |
ψ€ |
(q€, w) = |
ψ€ |
(q′, w) для всех |
|||||||||
w A |
+ |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
||||
|
. Отсюда по формуле (2) получаем, что ψ(q, w) =ψ(q , w) |
||||||||||||
при всех w A |
+ |
|
|
|
′ |
||||||||
|
. Следовательно, q ~ q . Отсюда следует, что |
||||||||||||
|
|
|
|
€ |
|||||||||
q€ = q′. |
|
|
|||||||||||
Итак, у автомата V |
неотличимыми являются только |
||||||||||||
совпадающие друг с другом состояния.
Автомат V = ( A,Q, B,ϕ,ψ) и приведённый автомат
€ |
€ |
V = |
( A,Q, B,ϕ€,ψ€) работают одинаково: для любой входной |
последовательности a(1)a(2)a(3) ... последовательность |
|
|
€ |
b(1)b(2)b(3) ... на выходе автомата V и автомата V одна и та же: |
|
b(1) =ψ(q, a(1)) =ψ€(q€, a(1)),
b(2) =ψ(q, a(1)a(2)) =ψ€(q€, a(1)a(2)) и т.д. (здесь q − начальное
состояние).
Типовые задачи
Пример 1. Построить приведённый автомат для автомата, заданного следующей диаграммой Мура, изображенной на рис. 3.14.
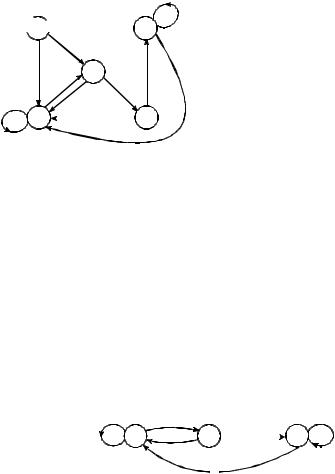
Решение. Вычислим: ψ(q1,0) =1, ψ(q2 ,0) =1, ψ(q3 ,0) = 0,
ψ(q4 ,0) =1, ψ(q5 ,0) =1. Следовательно, состояние q3 отличимо
 q1
q1
0,1
1,0 |
от всех остальных. Мы |
получаем (пока) следующее |
|
q2 |
разбиение множества |
Q ={q1, q2 , q3 , q4 , q5} на
1,1 |
,1 |
q3 |
0 |
|
1,0 |
|
классы, т.е. непересекающиеся |
|
|
0 |
|
, |
|
|
|
подмножества: |
|
|
0 |
0 |
|
|
Q ={q3} {q1, q2 , q4 , q5} |
|||
|
|
|
|
|
||||
1,1 |
|
|
, |
|
|
|
|
|
|
|
1 0,1 |
|
|
|
0,1 |
||
q4 |
|
|
|
|
q5 |
(далее это разбиение будет |
||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
измельчаться). |
|
|
|
Рис. 3.14. |
|
|
Далее вычисляем: |
||
|
|
|
|
|
ψ(q1,1) =1, ψ(q2 ,1) = 0, |
|||
|
|
|
|
|
|
|
|
|
ψ(q4 ,1) =1, ψ(q5 ,1) = 0. Отсюда следует, что q1 не может лежать в одном классе с q2 или q5 , q2 с q1 или q4 и т.д. Разбиение,
полученное ранее, измельчается до следующего:
Q ={q3} {q1, q4} {q2 , q5}. Положим K1 ={q3},
K2 = {q1, q4 }, K3 ={q2 , q5}. Покажем, что это окончательное разбиение. Имеем: ϕ(q1,0) = q3 , ϕ(q4 ,0) = q3 , поэтому
ϕ(K2 ,0) K1. Аналогично получаем ϕ(K2 ,1) K2 и т.д., т.е. функция ϕ “не разбивает” классы. Следовательно, классы K1, K2 , K3
можно считать состояниями нового автомата. Это и есть приведённый автомат, его диаграмма Мура изображена на рисунке 3.15.
1,1 |
0,1 |
|
|
0,0 |
1,0 |
K2 |
K1 |
|
K3 |
||
|
|
||||
|
1,0 |
0,1 |
|
|
|
|
Рис. 3.15. |
|
|
||

Пример 2. Построить приведённый автомат для автомата V , заданного следующей таблицей 3.6:
|
|
|
|
|
|
|
|
|
Табл. 3.6 |
|
|
q1 |
q2 |
|
q3 |
q4 |
|
q5 |
|||
0 |
q3 |
1 |
q1 |
1 |
q4 |
q1 |
1 |
q1 |
1 |
|
|
|
|
|
0 |
|
|
||||
1 |
q4 |
1 |
q5 |
0 |
q3 |
1 |
q4 |
0 |
q4 |
0 |
|
|
|
|
|
|
|||||
Решение. Верхняя строка таблицы 11011 определяет разбиение
σ: Q ={q3} {q1, q2 , q4 , q5}, нижняя строка − разбиение
τ: Q ={q1, q3} {q2 , q4 , q5}. Их пересечение σ ∩τ − это разбиение
Q ={q1} {q3} {q2 , q4 , q5}. Докажем, что состояния q2 , q4 , q5 неотличимы друг от друга. В столбцах таблицы, соответствующих этим
состояниям, мы имеем: 1 , 1 , 1 , значит, функция ψ на
0 0 0
состояниях q2 , q4 , q5 принимает одинаковые значения. Кроме того,
|
q |
|
q |
|
q |
|
|
|
другая часть столбцов: |
1 |
|
1 |
|
1 |
|
такова, что q5 |
, q4 , q4 лежат |
|
, |
, |
|
|||||
|
q5 |
|
q4 |
q4 |
|
|
|
|
в одном классе разбиения. Это доказывает, что q2 , q4 , q5 |
неотличимы. |
|||||||
Из таблицы автомата V теперь нетрудно получить таблицу
приведённого автомата € − для этого
V
достаточно взять по одному представителю в каждом классе разбиения σ ∩τ. Таким образом, мы получаем таблицу 3.7:
|
|
|
|
|
Табл. 3.7 |
|
|
q1 |
q2 |
q3 |
|||
0 |
q3 |
1 |
q1 |
1 |
q2 |
0 |
|
|
|
|
|||
1 |
q1 |
1 |
q2 |
0 |
q3 |
1 |
|
|
|
|
|||
|
Задачи для самостоятельного |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
решения |
|
|
|
|
|
|
|
|
|
|
|
|||
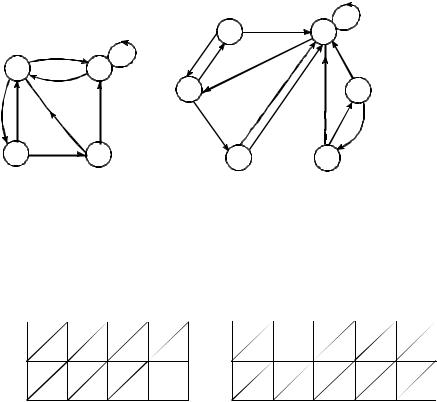
3. Автомат V задан диаграммой Мура. Построить диаграмму Мура |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
€ |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приведённого автомата V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
a,0 |
|
q2 |
|
|
a,0 |
|
|
|||
|
|
|
0,a |
|
|
|
|
1,a |
,1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
a,1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
, |
|
|
|
|
|
|
|
|
||
|
q1 |
|
|
0,b |
|
q2 |
|
|
|
b |
,0 |
b |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
q3 |
|
,1 |
|
|
a,1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
a |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1,a |
|
|
|
, |
|
1,a |
|
|
a |
|
|
,0 |
|
|
, |
|
|
|
|
||||
1,a |
|
b |
|
|
|
|
|
b |
|
|
|
|
|||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
b,1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
q3 |
|
|
|
|
q4 |
|
|
|
|
|
|
q4 |
|
|
|
q6 |
|
|
|
|||
|
|
0,a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Автомат V задан таблицей. Построить таблицу приведённого |
|
|
|
|
|||||||||||||||||||
|
|
€ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
автомата V |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Табл.3.8 |
|
|
|
|
|
|
|
|
|
|
|
Табл.3.9 |
||
|
|
|
q1 |
q2 |
|
q3 |
q4 |
|
|
q1 |
q2 |
q3 |
q4 |
|
q5 |
||||||||
|
0 |
q2 |
0 |
q1 |
0 |
q2 |
1 |
|
|
a |
q2 |
a |
q1 |
a |
q5 |
a |
q1 |
a |
q3 |
a |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
q1 |
1 |
q3 |
0 |
q4 |
|
1 |
|
|
b |
q5 |
b |
q4 |
a |
q2 |
b |
q3 |
b |
q4 |
a |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
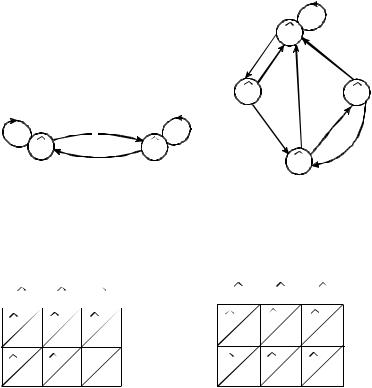
Ответ:
1.
1,a |
0,a |
1,a |
|
q1 |
|||
|
|||
0,b |
q2 |
||
|
|
а)
Рис. 3.18
|
|
|
|
q1 |
a,0 |
|
|
|
1 |
|
|
a |
|
||
|
|
|
|
|
|||
, |
|
|
|
, |
|
||
b |
|
|
,0 |
|
1 |
|
|
|
|
|
|
|
|||
q3 |
b |
a,1 |
q4 |
||||
|
|||||||
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
, |
|
||
a,1 |
|
|
b |
|
b,1 |
||
|
|
|
|
||||
|
|
|
|
q5 |
|
||
|
|
|
|
|
|
||
б)
2.
|
|
|
Табл. 3.10 |
|||
|
q1 |
q2 |
q3 |
|||
0 |
q2 |
0 |
q1 |
0 |
q2 |
1 |
|
|
|
|
|||
1 |
q1 |
1 |
q3 |
0 |
q1 |
1 |
|
|
|
|
|||
|
|
|
а) |
|
|
|
|
|
|
|
|
Табл.3.11 |
|
|
q1 |
q2 |
q4 |
|||
a |
q2 |
|
q1 |
|
1 |
|
a |
|
a |
q |
c |
||
|
|
|
|
|||
b |
q2 |
b |
q4 |
a |
q1 |
b |
|
|
|
|
|||
|
|
|
б) |
|
|
|
§3.5. Периодичность выходной последовательности конечного автомата

Мы докажем, что любой конечный автомат перерабатывает периодическую входную последовательность в периодическую выходную, период которой не превышает nτ, где τ − период входной
последовательности, а n =| Q | − количество состояний автомата.
Доказательство будет основываться на следующем (легко доказываемом) замечании: если входная последовательность имеет
период τ1, а последовательность состояний автомата – период τ2 , то
выходная последовательность будет иметь период НОК(τ1,τ2 ), где
НОК обозначает наименьшее общее кратное.
В теореме этого раздела и во многих других вопросах теории автоматов будет удобно использовать сокращённые обозначения для функций ϕ
и ϕ. А именно, пусть V = ( A,Q, B,ϕ,ψ) − автомат, q Q, a A и w A . Если q′ = ϕ(q, a), то этот факт мы будем записывать просто: q′ = qa. Аналогично этому вместо записи q′′ = ϕ(q, w) будем использовать сокращённую запись q′′ = qw.
Теорема. Если входная последовательность конечного автомата является периодической, то выходная последовательность также периодическая.
Доказательство. Пусть V = ( A,Q, B,ϕ,ψ) − конечный автомат.
Предположим, что на вход автомата поступает периодическая последовательность a(1)a(2)a(3).... Если τ − её период, то
a(t +τ) = a(t) при t ≥ t0 , где t0 − момент времени, с которого начинается период. Введём в рассмотрение следующие слова:
w = a(1)a(2) ... a(t0 −1) −
предпериод входной последовательности и
u = a(t0 )a(t0 +1) ... a(t0 +τ −1) −
период. Пусть q0 − начальное состояние автомата. Положим q = q0 w.
Рассмотрим последовательность состояний q, qu, qu2 , ... qun . Так как число членов этой последовательности равно n +1 >| Q |, то среди них есть совпадающие, т.е. существуют различные i, j ≤ n такие, что
qui = qu j . Можно считать, что j > i. Тогда j = i + m, где m > 0 и
