
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание
|
2 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
|
|
2 |
|
|
|
2 |
3 |
|
4 |
|||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
3 |
5 |
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Рис. 2.25 |
|
|
Рис. 2.26 |
|
|
|
|
Рис. 2.27 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
3 |
2 |
4 |
|
5 |
|
4 |
2 |
3 |
|
||||
|
|
|
|
Рис. 2.28 |
|
|
|
|
5 |
|
Рис. 2.29 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
5 







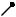 4
4


 6
6 1
1
Рис. 2.30
§2.3. Связность
Определение. Граф называется связным, если любые две несовпадающие вершины в нем соединены маршрутом.
Очевидно, для связности графа необходимо и достаточно, чтобы в нем для какой-либо фиксированной вершины и и каждой другой вершины v существовал (u, v)-путь.
Пусть задан граф G. Введем на множестве его вершин V(G) бинарное
отношение. Будем говорить, что vi |
~ v j , если существует путь из vi в |
v j . При этом будет считать, что vi |
~ vi , их соединяет путь нулевой |
длины. Введенное отношение является отношением эквивалентности. Следовательно, оно определяет разбиение множества вершин графа на

классы эквивалентности: V (G) =V1 V2 ... Vk . Обозначим через Gi подграф графа G , порожденный множеством вершин Vi . При этом
V (G) =V (G1) V (G2 ) ... V (Gk ) ,
E(G) = E(G1) E(G2 ) ... E(Gk ) , G = G1 G2 ... Gk .
Графы G1 , G2 , ..., Gk называются компонентами связности графа G .
Теорема. Для любого графа либо он сам, либо его дополнение является связным.
Доказательство. Пусть G – несвязный граф. А – одна из его компонент связности. Положим В = VG \ VA. Возьмем произвольную вершину и графа А. Тогда для любой вершины v из из множества вершин В в
дополнительном графе G есть ребро uv. Следовательно, произвольная вершина из В соединена с и. Если и1 – отличная от и вершина графа А, то для любой вершины v из множества вершин В в дополнительном
графе G также найдется ребро u1v. Таким образом найдется путь из вершины и в вершину u1 (через вершину v). Следовательно, из вершины
и в графе G достижима любая вершина, а значит, граф G является связным. Утверждение доказано.
Утверждение. Пусть G – связный граф, e EG . Тогда:
1)если ребро е принадлежит какому-либо циклу графа G, то граф G \ e связен;
2)если ребро е не входит ни в какой цикл, то граф G \ e имеет
ровно две компоненты связности.
Доказательство. 1). Пусть ребро e = uv принадлежит циклу Z
графа G. Заменив в каждой (x, y) -цепи, содержащей е, ребро е на цепь
Z \ e , получим путь, соединяющий вершины х и у, не содержащий ребра е. Следовательно, для любых двух несовпадающих вершин в графе G найдется (x, y) -путь, не включающий ребро е. Но тогда и граф
G \ e связен.
2) Пусть ребро е не входит ни в какой цикл графа G. Тогда, очевидно, вершины и и v входят в разные компоненты связности графа G \ e . Обозначим их через Gu и Gv соответственно. Для произвольной
вершины x ≠ u в G найдется (x, u) -путь. Если ребро е в этот путь не входит, то x Gu . В противном случае x Gv . Утверждение доказано.
Обозначим через Р количество ребер графа, В – количество вершин, K – количество компонент связности.
Определение. Число ν(G) = P − B + K называется цикломатическим
числом графа.
Теорема. Для любого графа G выполняется неравенствоν(G) ≥ 0.
Доказательство проведем индукцией по числу вершин п. При п = 1 получаем граф, состоящий из одной вершины, соответственно без ребер: P = 0, B =1, K =1, ν(G) = 0 . Неравенствоν(G) ≥ 0 выполнено.
Предположим, что при любом количестве вершин, меньшем п, утверждение верно и докажем его для графа с п вершинами. Обозначим их v1, v2 , ..., vn . Обозначим через G' подграф графа G , порожденный
вершинами v1, v2 , ..., vn−1 . Тогда ν(G' ) ≥ 0 по предположению индукции. Пусть P, B, K – количество ребер, вершин, компонент связности графа G ; P', B', K ' – графа G' ; k – количество ребер графа G , не являющихся ребрами графа G' , т.е. степень вершины vn . Тогда P = P'+k, B = B'+1 . Возможны два случая.
а) k = 0 , следовательно, вершина vn – изолированная. При этом
P = P', B = B'+1, K = K '+1 . Следовательно, P − B + K = P'−B'+K ' ,
ν(G' ) = ν(G) ≥ 0 .
б) k > 0 . Если при этом все k ребер, инцидентных вершине vn , соединяют ее с различными компонентами связности графа G' , то K = K '+1 − k , в остальных случаях K > K '+1 − k . Таким образом, K ≥ K '+1 − k . В итоге получаем
P − B + K ≥ P'+k − B'−1+ K '+1− k = P'−B'+K' , ν(G) ≥ν(G' ) ≥ 0 .
Теорема доказана.
Следствие. Для связного графа выполняется неравенство B ≤ P +1 .
Деревья
Определение. Связный граф без циклов называется деревом. Любой
граф без циклов называется
ациклическим (или лесом). Таким образом, компонентами связности леса являются деревья. На рис. 2.31
Рис.2.31
изображен лес, каждая компонента связности его является деревом. Теорема. Связный граф является деревом тогда и только тогда, когда число его вершин на единицу больше числа его ребер, т.е. B = P +1 . Доказательство. Необходимость. Заметим, что если граф G – дерево, то он имеет хотя бы одну вершину степени 1 (висячую вершину).
Действительно, предположим, что все вершины имеют степень, не меньшую 2. Возьмем произвольную вершину, обозначим ее v1 . Из нее
выходит по крайней мере два ребра. Найдется вершина v2 такая, что e1 = (v1, v2 ) EG . Так как степень вершиныv2 не меньше 2, то найдется вершина v3 , отличная от v1 , такая, что e2 = (v2 , v3) EG , и так далее.
Так как число вершин конечно, то в этой последовательности вершин найдутся совпадающие, и мы получим цикл, что противоречит определению дерева. Следовательно, висячая вершина существует. Далее доказательство проведем индукцией по числу вершин п. При п = 1 число ребер равно 0 и утверждение верно. Предположим оно верно при любом количестве вершин, меньшем п. Рассмотрим граф G с п вершинами. Среди них есть висячая. Рассмотрим подграф G', порожденный множеством остальных вершин. Для него по индукционному предположению P' = B'−1 . Кроме того,
P = P'+1, B = B'+1 . Следовательно, P = B −1 . Необходимость доказана.
Достаточность. Пусть для связного графа G выполняется условие P = B −1 . Для того, чтобы доказать, что G является деревом, нужно показать лишь отсутствие циклов. Предположим, что циклы есть, тогда удаление одного ребра е из цикла не нарушает связности, граф
G' = G \ e
тоже связный. Следовательно, для него выполняется неравенство P' ≥ B'−1. Но P' = P −1, B' = B , следовательно, P ≥ B и значит,
P > B −1 , что противоречит условию. Следовательно, G является связным графом без циклов, т.е. деревом. Теорема доказана.
Свойства деревьев.
1.Любые две вершины дерева можно соединить путем. Если это простой путь, то он единственный.
2. Если для некоторого дерева G V(G) ≥ 2, то оно имеет не менее двух висячих вершин.

Кодировка дерева
Существуют способы задания деревьев, более экономичные, чем с помощью матриц смежности и инцидентности, которые в компьютере
занимают много памяти. |
1 |
|
Первый способ кодирования. Пусть Т – дерево, |
||
n =| E(T ) |=|V (T ) | −1. Поставим в соответствие |
|
|
дереву Т с п ребрами слово, состоящее из 0 и 1 |
|
|
длиной 2п следующим образом. Выберем |
|
|
произвольно вершину и начнем обход дерева по |
|
|
|
|
|
произвольному ребру так, чтобы ребра все время |
|
|
оставались справа, поворачивая в висячих |
|
|
вершинах. Если ребро встретилось в первый раз, |
|
|
|
|
|
записываем 0, во второй – 1. Код дерева, |
Рис. 2.32 |
|
представленного на рис.2.32 – (010010101101) |
||
(обход начат с вершины 1). |
|
|
Заметим, что дереву с одним ребром сопоставляется код (01). Если
~
деревьям Т1 и Т2 (рис.2.33, а) сопоставлены коды α~ и β соответственно, то дереву С (рис. 2.33, б) сопоставляется код (0 α~ 1), а
C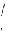
 T1
T1

T1 |
T2 |
C c |
|
D |
T1 |
T2 |
T2 |
T1 |
|
||||||||
|
|
|
|
|
|
E |
|
|
a |
b |
c |
c=a=b |
c=a=b |
||||
|
а) |
б) |
|
|
в) |
|
||
|
|
|
|
Рис. 2.33 |
|
|
|
|
|
|
~ ~ |
~ ~ |
|
|
|
||
деревьям D и E (рис. 2.33, в) – коды αβ |
и βα . |
|
|
|
||||
Не всякая последовательность из п единиц и п нулей служит кодом дерева. Необходимым и достаточным условием для этого служит следующее: в любом начальном отрезке последовательности количество нулей не меньше количества единиц. Если это условие выполняется, дерево может быть построено по коду.
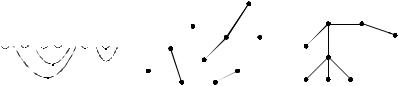
Построение дерева по коду
Для того чтобы восстановить дерево по коду, нужно разбить последовательность на пары из нулей и единиц, соответствующие одному и тому же дереву. Первая попавшаяся в коде единица образует пару с предшествующим нулем. Каждая следующая образует пару с ближайшим слева неиспользованным нулем. Пометим пары снизу дугами, которые соответствуют ребрам графа, занумеровав их. Например, если дан код (010010010111010011), поступим так (см. рис. 2.34а). Дерево, соответствующее этому коду, изображено на рис. 2.34б.
|
|
|
|
|
|
4 3 |
1 |
2 |
|
||
(010010010111010011) |
|
|
|
1 |
|||||||
|
|
|
|
||||||||
5 |
4 |
1 2 |
8 |
6 |
|
5 |
|
|
|
|
|
|
|
3 |
|
7 |
|
|
|
|
|
||
|
|
|
9 |
8 |
6 |
|
|
||||
|
|
9 |
|
|
|
|
|
5 |
|||
|
|
|
|
7 |
|
||||||
2 |
3 |
|
8 |
4 |
|
6 |
7 |
а) |
б) |
Рис. 2.34 |
Рис. 2.35 |
Второй способ кодирования
Перенумеруем вершины дерева произвольным образом (рис.2.35). Найдем висячую вершину с наименьшим номером. Запишем номер единственной смежной с ней вершины и удалим висячую вершину вместе с ребром. Для получившегося дерева снова найдем висячую вершину с наименьшим номером и т. д., пока не останется одно ребро. Длина кода при этом равна |E| – 1 = |V| – 2.
Пример. Построить код дерева, изображенного на рис. 2.35. Висячая вершина с наименьшим номером – 1, смежная с ней – 2.
Удаляем вершину 1 вместе с ребром и записываем в код 2. В оставшемся дереве висячая вершина с наименьшим номером – 5, смежная с ней – 4. Удаляем вершину 5 вместе с ребром и записываем в код 4. В оставшемся дереве висячая вершина с наименьшим номером – 6, смежная с ней – 4. Удаляем вершину 6 вместе с ребром и снова записываем в код 4. В оставшемся дереве висячая вершина с наименьшим номером – 7, смежная с ней – 4. Удаляем вершину 7 вместе с ребром и снова записываем в код 4. В оставшемся дереве
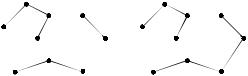
висячая вершина с наименьшим номером – 4, смежная с ней – 2. Удаляем вершину 4 вместе с ребром и записываем в код 2. В оставшемся дереве висячая вершина с наименьшим номером – 2, смежная с ней – 3. Удаляем вершину 2 вместе с ребром и записываем в код 3. Осталось одно ребро. Получили код дерева [244423].
Восстановление дерева по коду рассмотрим на примере кода
[2557389]. Вместо первого числа в коде пишем наименьшее, не встречающееся в коде: 1557389. Вместо второго числа в новой последовательности пишем наименьшее, не встречающееся в ней: 1257389 и т.д. Получаем последовательность 1245637. Расположив ее под кодом, получим список ребер: (2,1), (5, 2), (5, 4), (7, 5), (3,6), (8,3),
2 |
|
|
2 |
|
|
|
(9, 7). Строим |
сначала |
||
5 |
7 |
|
|
7 |
граф по |
этому |
списку |
|||
|
5 |
|
||||||||
1 |
|
9 |
1 |
|
|
9 |
ребер |
(рис.2.36). |
В |
|
|
|
|||||||||
4 |
|
4 |
|
|
последовательности |
|||||
3 |
|
3 |
|
|
1245637 |
отсутствуют |
||||
6 |
8 |
|
|
|||||||
|
6 |
|
|
8 |
числа 8 и 9. Соединяем |
|||||
|
|
|
|
|
вершины 8 и 9 ребром и |
|||||
|
|
|
|
|
|
|||||
Рис. 2.36 |
|
Рис.2.37 |
|
|||||||
|
|
получаем граф (рис. |
||||||||
|
|
|
|
|
|
|
2.37). |
|
|
|
Можно показать, что между помеченными деревьями (т.е. деревьями с пронумерованными вершинами) и последовательностями
ε1, ε2 , ..., εn−2 , где 1 ≤ εi ≤ n, существует взаимно однозначное
соответствие. Поэтому количество помеченных деревьев равно nn−2
(формула Кэли).
Эйлеровы пути. Эйлеровы циклы
Определение. В графе G путь из а в b называется эйлеровым путем, если он содержит все ребра графа, причем каждое по одному разу. Эйлеров цикл – путь из а в а, который содержит все ребра графа, каждое по одному разу. Гамильтонов путь – путь, обходящий все вершины графа по одному разу. Гамильтонов цикл – путь из а в а, обходящий все вершины графа, кроме а, по одному разу.
Теорема. Пусть дан связный граф. В нем существует эйлеров путь тогда и только тогда, когда две вершины графа имеют нечетную степень, а все остальные – четную. Эйлеров цикл существует тогда и только тогда, когда все вершины графа имеют четную степень.

Доказательство. Доказательство обеих частей теоремы проведем одновременно.
Необходимость. Пусть в графе G существует эйлеров
путь из а в b. Тогда d(a) –
нечетное число. Действительно, |
|
|
из а выходит по крайней мере |
|
|
одно ребро, обозначим его е1 . |
|
|
Если путь возвращается в а по |
а) |
б) |
ребру е2, то он должен и |
|
Рис. 2.38 |
выходить из него по ребру е3, и так далее (рис. 2.38,а). Степень вершины а – нечетная. Аналогично для
вершины b. Если путь из а в а – эйлеров цикл, то первое и последнее ребро цикла инцидентны а. Если вершина а встречается внутри цикла, то вместе с ребром (vi , a) он содержит и ребро (a, vk ) . Степень
вершины а – четная. Остальные вершины являются внутренними и для эйлерова пути, и для эйлерова цикла, поэтому, если путь или цикл содержит ребро (vi , v j ) , то он содержит и ребро (v j , vk ) , если v j ≠ b .
Так как все ребра в пути и цикле встречаются ровно один раз, то степень вершины v j – четная (рис.2.38,б).
Достаточность. Доказательство проведем индукцией по количеству ребер. Пусть d(a) , d(b) – нечетные. Наименьшее
количество ребер равно 1. При этом граф G состоит из двух вершин а и b и соединяющего их ребра, который и будет
являться эйлеровым путем. Если степени всех вершин четные, то наименьшее количество ребер равно трем (при отсутствии кратных
ребер). Если степени всех вершин четные, возможен только граф, изображенный на рис.
2.39. Эйлеров цикл существует. Предположим, для графа с количеством ребер, меньшим п, утверждение истинно. Докажем утверждение
для графа с п ребрами. Удалим произвольное ребро, выходящее из а. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. Если удалено ребро (а, b), то степени всех вершин нового графа четны, граф связный, и по индукционному предположению, в нем существует эйлеров цикл. Его можно начинать из произвольной
вершины. Для нового графа рассмотрим эйлеров цикл из b в b. Присоединив к нему ребро (а, b) (если нужно, вместе с вершиной а), получим эйлеров путь из b в а в исходном графе.
Если произвольное ребро, выходящее из а, – это ребро (а, с),
c ≠ b , то, удалив его, получим, что степень вершины а стала четной, а степень вершины с – нечетной, число ребер уменьшилось на 1. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. В новом графе G' также две вершины с четными степенями (b и с), остальные – с нечетными степенями. По предположению индукции в G' существует эйлеров путь из с в b. Добавив к нему ребро (а, с), получим эйлеров путь из а в b.
Докажем теперь утверждение для эйлерова цикла с п ребрами. Пусть связный граф G имеет вершины только с четными степенями. Удалив из него одно ребро, например, (а, b) , получим граф G', у которого степени двух вершин нечетны, остальные – четны. Предположим, что удаление ребра нарушило связность графа, т.е. у графа G' две компоненты связности G1 и G2, при этом вершины с нечетными степенями а и b находятся в разных компонентах связности. Тогда сумма степеней вершин для каждого из графов G1 и G2 нечетна, чего не может быть. Следовательно, граф G' – связный, и по индукционному предположению в нем существует эйлеров путь из а в b. Добавив к эйлерову пути ребро (а, b), получим эйлеров цикл. Теорема доказана.
Теорема о цикломатическом числе
Напомним, что цикломатическим числом графа G называется число ν(G) = P − B + K , где P – число ребер, B – число вершин, K – число
компонент связности графа G. Было доказано, что для любого графа ν(G) ≥ 0 , для дерева ν(G) = 0 .
Теорема. Если граф G состоит из нескольких компонент связности
G1, G2 , ..., Gk , то ν(G) = ν(G1) + ν(G2 ) +... + ν(Gk ) .
Доказательство. Так как графы G1, G2 , ...,Gk – связные графы, то
ν(G1) = P1 − B1 +1, ν(G2 ) = P2 − B2 +1 , …, ν(Gk ) = Pk − Bk +1.
Сложив почленно эти равенства, получим
k
∑ν(Gi ) = P − B + K = ν(G) . теорема доказана.
i=1
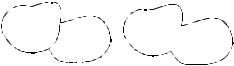
Введем определение суммы циклов произвольного графа. Пусть С1 и С2
– произвольные циклы графа G, содержащие общие участки пути, соединяющие вершины
vi и vi |
2 |
, vi |
3 |
и vi |
4 |
и так |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
далее. Тогда суммой |
|
|
|
|
|||||||
циклов С1 и С2 будем |
|
|
|
|
|||||||
называть граф, |
|
|
C1 |
|
|
|
|||||
вершинами которого |
|
|
|
||||||||
C1 |
C1+C2 |
||||||||||
|
|||||||||||
являются все вершины |
|
||||||||||
|
|
|
Рис. 2.40 |
||||||||
циклов С1 и С2, за |
|
|
|
|
|||||||
исключением внутренних вершин их общих участков, а ребрами – все их ребра, за исключением ребер, составляющих их общие участки (рис. 2.40). Если циклы С1 и С2 не имеют общих участков, то их суммой
называется объединение циклов С1 + С2 = С1 С2. Вообще говоря, сумма двух циклов, даже и имеющих общие ребра, может не являться сама циклом, но является объединение простых циклов. Далее под циклом везде подразумевается либо простой цикл, либо объединение простых циклов.
Очевидно, что C +C = , C + = C . По сложению циклы образуют абелеву группу.
Если граф G имеет т ребер е1, е1, … ет, то любому циклу С графа G можно поставить в соответствие двоичный код длины т:
1, еслиei входит вC, C → (ε1ε2...εm ) , εi = 0, еслиei невходит вC.
Если циклу С1 соответствует код (ε1,ε2 ,...,εm ) , а циклу С2 – код (η1, η2 ,..., ηm ) , то циклу С1 + С2 соответствует код
(ε1 + η1, ε2 + η2 ,..., εm + ηm ) , где сложение производится по модулю 2. Таким образом, множество циклов графа G можно рассматривать, как
подгруппу группы Z2 × Z2 × Z2 × ...× Z2 . Циклы образуют линейное
1444244443 m раз
пространство над полем Z2 .
Теорема. Пусть дан произвольный граф G (без петель, без кратных ребер, с конечным числом вершин) и ν(G) = k . Тогда:
1)Из графа G можно удалить k ребер так, что оставшийся граф будет без циклов и будет иметь столько же компонент связности, что и G.
2)Размерность пространства циклов графа G равна k.
Доказательство. 1° . Докажем, что ν(G) = 0 тогда только тогда, когда в графе G нет циклов. Действительно, если ν(G) = 0 , а
G1, G2 , ..., Gs – компоненты связности графа G, то
ν(G) = ν(G1) + ν(G2 ) +... + ν(Gk ) = 0 . Так как
ν(G1) ≥ 0, ν(G2 ) ≥ 0, ..., ν(Gs ) ≥ 0 , то ν(Gi ) = 0 при всяком i =1, 2, ..., s .
Имеем ν(Gi ) = Pi − Bi +1 , следовательно, Gi – дерево, а значит, в Gi нет
циклов. Таким образом, в графе G тоже нет циклов. Докажем, что если в графе G нет циклов, то ν(G) = 0 .
Действительно, тогда G – лес, ν(G) = ν(G1) + ν(G2 ) +... + ν(Gk ) , где ν(G) = 0 , G1, G2 , ..., Gs – компоненты связности графа G, т.е. деревья.
Так как для дерева ν(Gi ) = 0 , то ν(G) = 0 .
Таким образом, мы доказали, что если для графа G ν(G) = 0 , то в
нем нет циклов.
Пусть теперь ν(G) = k > 0 . Тогда в G есть циклы. Возьмем произвольно цикл С1, е1 – произвольное ребро этого цикла. Тогда граф G \ e1 имеет
то же количество компонент связности, что и G.
ν(G \ e1) = ν(G) −1 = k −1 . Если k −1 = 0 , то полученный граф будет без циклов. Если k −1 > 0 , то аналогично берем цикл С2 и ребро е2 и т.д. Этот процесс состоит ровно из k шагов. На каждом шаге количество компонент связности не меняется. Граф G \ {e1, e2 , ..., ek } является
лесом, количество компонент связности у него такое же, как и у G. 2° . Занумеруем остальные ребра графа G:
E(G) ={e1, e2 , ..., ek , ek +1, ..., em} . Тогда циклам С1, С2, …, Сk
соответствуют коды
C1 → (1, , , . . ., ), C2 → (0, 1, , . . ., ),
...,
Ck → (0, 0, ..., 0, 1, , . . ., ).
14243
k
Строки кодов линейно независимы. Осталось доказать, что любой цикл графа G можно линейно выразить через циклы С1, С2, …, Сk.. Возьмем произвольный цикл С с соответствующим ему кодом
C → (ε1, ε2 ,..., εk , εk +1, ..., εm ) . Строки (1, , ..., ),
(0, 1, , ..., ),
..., (0, 0, ..., 1)
линейно независимы, следовательно, образуют базис в пространстве размерности k. Поэтому
(ε1, ε2 ,..., εk ) = λ1(1, , ..., ) + λ2 (0, 1, 0, ..., ) +... + λk (0, 0, , ..., 1)
при некоторых λ1, λ2 , ..., λk {0,1} . Рассмотрим цикл
C' = C + λ1C1 + λ2C2 +... + λkCk .
Учитывая, что (ε1, ε2 ,..., εk ) + (ε1, ε2 ,..., εk ) = (0,0,...,0) , получаем C' = (ε1, ε2 ,..., εk , εk +1, ..., εm ) +
+λ1(1, , ..., ) + +λ2 (0, 1, 0, ..., ) +... +
+λk (0, , 0, 1, , ..., ) = (0, ,0, ...0, , ..., ).
Таким образом, C' – цикл в графе G \ {e1, e2 , ..., ek } . Но по построению, G \ {e1, e2 , ..., ek } – граф без циклов. Следовательно, C' = (0, 0, ..., 0) и
C + λ1C1 + λ2C2 +... + λkCk = (0, 0, ..., 0) , значит,
C = λ1C1 + λ2C2 +... + λkCk .
Теорема доказана.
Если G – связный граф и ν(G) = k , то по только что доказанной теореме
из G можно удалить некоторые k ребер так, чтобы получилось дерево Т. Назовем его остовным деревом графа G. Аналогично, если G – несвязный граф, то из G можно удалить некоторые k ребер так, чтобы
получился граф без циклов, т.е. лес, называемый остовным лесом графа G.
Решение типовых задач
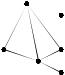
1. Существует ли Эйлеров цикл у графа, |
1 |
2 |
|
изображенного на рис. 2.41? Если существует, |
|
||
построить его. |
|
|
|
Решение. Так как степени всех вершин четны, |
3 |
4 |
|
тот эйлеров цикл существует. Возьмем |
5 |
6 |
|
произвольный цикл, например, (1, 5, 3, 1). Этот |
|||
|
|
||
цикл не содержит все ребра графа. Рассмотрим |
Рис. 2.41 |
|
|
граф, полученный из исходного удалением этого |
|
|
цикла. Удаленный граф и оставшийся, в силу связности исходного графа всегда имеют общую вершину, в данном случае – 5. Рассмотрим теперь произвольный цикл нового графа, начинающийся в вершине 5, например, (5, 4, 6, 5). Присоединим его к первому циклу: (1, 5, 4, 6, 5, 3, 1). Остается единственный цикл (4, 1, 2, 4), присоединив который,
получим эйлеров цикл (1, 5, 4, 1, 2, 4, 6, 5, 3, 1).
2. Найти число компонент связности леса, который имеет 40 вершин и 23 ребра.
Решение. Так как для леса ν(G) = 0 , получаем P − B + K = 0 ,
K= B − P =17 .
3.Чему может равняться число ребер графа, имеющего 20 вершин и 4 компоненты связности?
Решение. Так как ν(G) ≥ 0 , имеем P − B + K ≥ 0 , следовательно,
P ≥16 . Покажем, что найдется граф, для которого P =16 , B = 20 ,
K = 4 . Пусть 3 компоненты связности – изолированные вершины, четвертая – простая цепь С17 с 16 ребрами. Таким образом, минимальное число ребер равно 16. Выясним, каким может быть максимальное число ребер.
Докажем, что наибольшее количество ребер у графа, три компоненты связности которого представляют собой изолированные вершины, четвертая – полны граф К17 с числом ребер, равным 136. Действительно, рассмотрим граф с 20 вершинами и 4 компонентами связности
G1, G2 ,G3 , G4 , из которых по крайней мере 2 содержат не менее двух вершин. Предположим, что V1 ≥V2 ≥1. Возьмем произвольно вершину из V2 , удалим все ребра, инцидентные ей, и соединим ее ребрами со
всеми вершинами из V1 . Новый граф будет иметь то же количество
вершин и компонент связности, но больше ребер. Таким образом, количество ребер может быть от 16 до 136.
4. Чему может равняться число компонент связности графа, имеющего 12 вершин и 27 ребер?
Решение. Так как простая цепь С12 имеет 11 ребер, а полный граф К12 – 66 ребер, то существует связный граф, имеющий 12 вершин и 27 ребер. Минимальное число компонент связности равно 1. Для того, чтобы определить максимально возможное число компонент связности, найдем наименьший полный граф, число ребер которого не меньше 27: n(n −1) / 2 ≥ 27, n = 8 . Рассмотрим граф, 4 компоненты связности
представляют собой изолированные вершины, а пятая имеет 8 вершин и 27 ребер. Докажем, что 6 компонент связности быть уже не может. Действительно, по предыдущей задаче, граф, имеющий 12 вершин и 6 компонент связности, может иметь не более 21 ребра. Таким образом Таким образом, количество компонент связности может быть от 1 до 5. 5. Для графа, изображенного на рис.2.42(а) найти цикломатическое число, укзать базис циклов,
построить остовное дерево. |
|
|
e2 |
e1 |
|
|||
Для данного графа B = 9 , P =11 , |
e3 |
|
e4 |
|
|
|
||
|
|
|
|
|
||||
K =1. Следовательно, ν(G) = 3 и из |
|
e5 |
|
|
|
|||
G надо удалить три ребра, чтобы |
|
|
|
|
|
|
|
|
e6 |
|
e11 |
e7 |
|
|
|
||
получилось дерево. Базис циклов |
|
|
|
|
||||
также состоит из трех циклов. |
e9 |
|
|
|
|
|
|
|
|
e10 |
|
|
|
||||
Выберем произвольно цикл, |
|
|
|
|
||||
например, C1 = {e2 , e4 , e5 , e3} . |
|
|
а) |
|
|
|
б) |
|
|
|
|
|
|
|
|||
Удалим из графа ребро е2. В |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
получившемся графе возьмем цикл |
|
|
|
Рис 2 42 |
|
|||
C2 ={e5 , e7 , e11, e6}. Удалим из
графа ребро е5. В получившемся графе возьмем цикл C3 ={e9 , e10 , e11} .
Удалим из графа ребро е10. Получим остовное дерево графа G , изображенное на рис. 2.42б). Циклы С1, С2, С3 образуют базис. Разложим какой-нибудь цикл, например, C4 = {e2 , e3, e6 , e9 , e10 , e7 , e4} , по этому базису. Запишем коды циклов:
C1 = (01111000000), C2 = (00001110001),
C3 = (00000000111), C4 = (01110110110).
Так как были удалены ребра е2, е5, е10, то в матрице, составленной из кодов циклов С1, С2, С3, С4, базисным будет минор, составленный из
|
1 |
0 |
0 |
|
|||
|
|
0 |
1 |
1 |
|
|
|
столбцов под номерами 2, 5, 10: |
|
|
. |
||||
|
0 |
0 |
1 |
|
|||
|
|
||||||
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
||||
Отсюда получаем C4 = C1 + C3 .
Задачи для самостоятельного решения
1.Сколько компонент связности имеет граф со следующим набором степеней вершин: 1, 1, 1, 2, 2, 2, 2, 3?
2.Изобразить граф G = Z3 ×C2 . Найти ν(G) , построить базис
циклов.
3. Изобразить граф G = Z3 ×C3 . Найти ν(G) , построить базис циклов.
4.Построить базис циклов графа K4 .
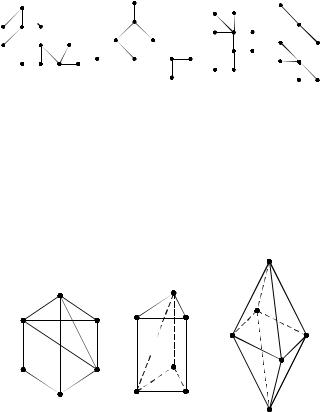
5.Построить базис циклов графа B3 .
6.Построить базис циклов графа B4 .
7.Построить базис циклов графа K3,3 .
8.Является ли деревом прямое произведение деревьев?
9.Найти число компонент связности леса, который имеет 76 вершин и 53 ребра.
10.Сколько ребер имеет лес с 10 вершинами, если он имеет 3 компоненты связности?
11.Чему может равняться число компонент связности графа, имеющего 15 вершин и 35 ребер?
12.Чему может равняться число компонент связности графа, имеющего 12 вершин и 20 ребер?
13.Чему может равняться число ребер графа, имеющего 10 вершин и 3 компоненты связности?
14.Доказать, что если граф имеет 10 вершин и 37 ребер, то он связен.
15.Доказать, что если граф имеет 8 вершин и 23 ребра, то он связен.
16.Связный граф имеет 12 вершин. Сколько он может иметь ребер?
17.Сколько ребер может быть у связного графа с п вершинами?
18.Сколько всего неизоморфных деревьев с пятью вершинами? Изобразить их.
19.Сколько всего графов с 12 вершинами и 65 ребрами? с 64 ребрами?
а) |
б) |
в) |
г) |
Рис. 2.43
20.Построить коды деревьев (два для каждого дерева), изображенных на рис.2.43.
21.Построить дерево по коду (00101001011101).
22.Построить дерево по коду (00101011001101).
23.Построить дерево по коду [5345566].
24.Построить дерево по коду [4445477].
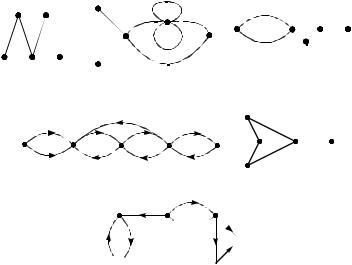
25.У каких из графов, изображенных на рис.2.44, существует эйлеров путь или эйлеров цикл? Если существует, то построить его.
а) |
б) в)
Рис. 2.44

Ответы
1. 1 или 2. Указание: рассмотреть, сколько вершин может быть в каждой компоненте связности. 2. См. рис. 2.45. ν(G) = 4 . Базис циклов:
(1, 2, 3), (1, 3, 6, 4), (3, 2, 5, 6), (1, 2, 5, 4). 3. ν(G) = 7 . 4. ν(G) = 3 .
|
|
|
|
|
|
|
|
|
|
5. |
ν(G) = 5 . |
|
|
|
|
|
|
|
|
|
|
|
6. |
ν(G) =17 . |
|
|
|
|
|
|
|
|
|
|
|
7. |
ν(G) = 4 . |
|
|
|
|
|
|
|
|
|
|
|
8. |
Не |
является |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
(см. рис. 2.12). |
||
|
|
|
|
|
|
|
|
|
|
|||
Рис. 2.45 |
|
|
|
|
|
Рис. 2.46 |
9. 23. |
10. 7. 11. |
||||
|
|
|
|
|
|
|
|
|
|
От 1 |
до 7. 12. |
|
От 1 до 6. 13. От 7 до 28. 14. Указание. Доказать, что несвязный граф с 10 вершинами имеет не более 36 ребер. 15. Указание. Доказать, что несвязный граф с 8 вершинами имеет не более 21 ребра. 16. От 11 до 66. 17. От n −1 до n(n −1) / 2 . 18. 3 , см рис. 2.46. Указание. Рассмотреть
возможные наборы степеней вершин. 19. Один, два. 20. При нумерации,
указанной на рис. 2.47: а) (01000010110101101101), [114457557]; б) (0000101110010111); [2332477]; в) (0010100101011011), [ 4444666];
г) (00001010101111), [246666]. 21. См. рис. 2.48а . 22. См. рис. 2.48б. 23.
См. рис.2.48в 24. См. рис.2.48г. 25. а), в) – существует; б) нет.
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
2 |
|
|
1 |
|
|||||
3 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
5 |
|
||||||
|
|
8 |
3 |
4 |
|
|
|
|
3 |
|
|
3 |
|
|||||||||||
6 |
4 |
5 |
|
|
|
|
|
|
|
|
7 |
4 |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
7 |
8 |
6 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
9 |
|
|
|
|
|
5 |
6 |
|
|
|
|
|
|
|
|
|
9 |
|
|
5 |
6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
10 |
7 |
11 |
|
9 |
|
|
|
|
8 |
|
|
|
8 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
7 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
б) |
|
|
|
|
|
в) |
|
|
г) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.47 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
б) |
в) |
г) |
|
Рис. 2.48 |
|
|
