
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание

§3.7. Ограниченно-детерминированные функции. Информационное дерево
Пусть A − множество. Каждую бесконечную последовательность
a(1)a(2)a(3)... , где a(i) A, будем называть сверхсловом.
Обозначим через A∞ множество всех таких сверхслов. Пусть A, B − два конечных множества, их мы будем называть алфавитами.
Рассмотрим отображение f : A∞ → B∞. Это отображение можно интерпретировать как воображаемое устройство, перерабатывающее сверхслова в алфавите A в сверхслова в алфавите B.
a(1)a(2)a(3)... b(1)b(2)b(3)...
f
Рис. 3.19
Выясним, каким условиям должна удовлетворять функция f , чтобы
она могла быть реализована некоторым автоматическим устройством. Если это устройство работает в дискретном режиме времени, получая в
момент времени i символ a(i) и выдавая символ b(i), то должен быть выполнен закон причинности (“причина предшествует следствию”); в нашем случае это означает, что может зависеть от
a(2), ... , a(i), но не должно зависеть от a(i +1), a(i + 2), ... . Исходя из этого, сформулируем определение детерминированной функции. Определение. Функция f : A∞ → B∞ называется
детерминированной (или д-функцией), если выполнено условие:
для любого i и для любых сверхслов w = a(1)a(2)a(3)..., w′ = a′(1)a′(2)a′(3)..., если f (w) = b(1)b(2)b(3)...,
f (w′) = b′(1)b′(2)b′(3)... и a(1) = a′(1), ... , a(i) = a′(i), то b(i) = b′(i).
Итак, детерминированная функция характеризуется тем, что b(i) является функцией лишь от a(1), a(2), ... , a(i) :
b(i) = fi (a(1), a(2),..., a(i)).
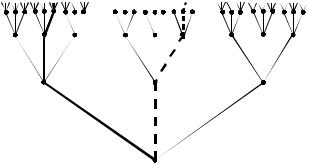
С множеством A∞ можно связать некоторое бесконечное дерево T. Опишем его построение. Пусть A ={a1, a2 , ... , am}. Возьмём любую
точку и назовём её корнем дерева. Из корня выпустим m рёбер, концы которых назовём вершинами первого яруса. Из каждой вершины первого яруса выпустим m рёбер, которые назовём вершинами второго яруса. И т.д. (см. рис. 3.20).
. . . . . . . . . . . . . . . . . . . . . . .
Рис. 3.20
Ветви дерева T (бесконечные) соответствуют сверхсловам
a(1)a(2)a(3)... A∞ , причём это соответствие взаимно однозначное. Будем считать, что рёбра, соответствующие буквам алфавита
A ={a1, a2 ,..., am}, идут слева направо (т.е. крайнее левое ребро соответствует букве a1, следующее – букве a2 , крайнее правое – букве am ). На рисунке изображено дерево, построенное для трёхбуквенного алфавита A ={a,b, c}. Ветвь дерева, отмеченная жирной линией, соответствует сверхслову abcb..., а ветвь, отмеченная пунктирной линией, – сверхслову bcbb...
Пусть дана детерминированная функция f : A∞ → B∞. Построим
дерево T, соответствующее множеству A∞ , и пометим его рёбра буквами алфавита B, как будет показано ниже. Рассмотрим произвольное сверхсловоw = a(1)a(2)a(3)... A∞. Пусть
f (w) = b(1)b(2)b(3)... Рассмотрим ветвь дерева T, соответствующую сверхслову w, и пометим рёбра этой ветви символами
b(1),b(2),b(3),... Так поступим с каждой ветвью. Если у двух сверхслов w = a(1)a(2)a(3)... и w′ = a′(1)a′(2)a′(3)... совпадут первые k букв: a(1) = a′(1), ..., a(k) = a′(k), то ввиду детерминированности функции f у сверхслов f (w) и f (w′) также
будут совпадать первые k букв. Следовательно, в процессе расстановки пометок на рёбрах мы не получим противоречия (т.е. каждое ребро дерева T получит ровно одну пометку). Дерево T, рёбра которого помечены вышеописанным способом, назовём информационным деревом, соответствующим функции f , и
обозначим его T f . Наоборот, если дано дерево T для A∞ , то,
пометив его рёбра буквами из B произвольным образом, мы получим информационное дерево, соответствующее некоторой функции f .
Очевидно, соответствие между информационными деревьями и детерминированными функциями является взаимно однозначным.
Детерминированность функции f : A∞ → B∞ является необходимым условием реализуемости функции f некоторым автоматическим
устройством. Но она не является достаточным условием. Причина в том, что всякое механическое устройство имеет конечную память (т.е. может хранить ограниченное количество единиц информации). Рассмотрим эти соображения более подробно.
Пусть дано информационное дерево T f , соответствующее детерминированной функции f (см. рис. 3.21). Для любой вершины v этого дерева пусть T f (v) обозначает поддерево, корнем которого
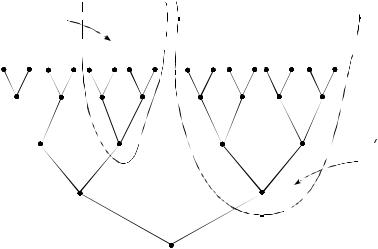
является вершина v (оно состоит из вершины v и всех вершин и рёбер, идущих “после” v, вместе с пометками на этих рёбрах).
Tf (v) 


. . . . . . . . . . .
. . . . .  .
.  . . . . . . . . . . .
. . . . . . . . . . .
v |
Tf (v ) |
|
|
|
v |
Рис. 3.21
Введём отношение эквивалентности ~ на множестве вершин дерева T f ,
полагая v ~ v′, если у деревьев T f (v) и T f (v′) соответствующие друг другу рёбра имеют одинаковые пометки. Детерминированная функция f : A∞ → B∞ называется ограниченно детерминированной
(или о.д.-функцией), если множество вершин информационного дерева T f разбивается на конечное число ~ -классов.
Пример. Пусть функция f :{0, 1}∞ →{0, 1}∞ определяется правилом f (a(1)a(2)a(3) ...) = a(1), a(1) + a(2), a(1) + a(2) + a(3), ... (здесь +
обозначает сложение по модулю 2). Информационное дерево имеет вид
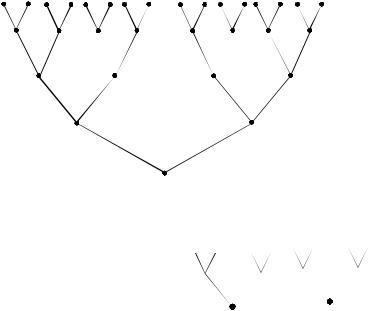
. . . . . . . . . . . . . . . . . . . . . . .
0 |
1 |
1 |
0 0 |
1 1 |
0 |
0 |
1 1 |
0 0 |
1 |
1 |
0 |
|
0 |
|
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
|
|
0 |
|
1 |
|
|
1 |
0 |
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
Рис. 3.22 |
|
|
|
|
|
|
Можно заметить (и это легко |
|
|
|
|
|
|
|
||||
проверяется), что все вершины |
|
|
|
|
|
|
|||||
вида, изображенного на рис. 3.23а в |
|
|
|
|
|
|
|||||
этом дереве эквивалентны друг |
|
|
|
|
|
|
|||||
другу, и аналогичное справедливо |
|
0 |
1 |
|
1 |
0 |
|||||
для вершин вида, изображенного на |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
рис. 3.23б. Таким образом, функция |
|
|
а) |
|
|
б) |
|||||
f данного примера является |
|
|
|
|
|||||||
ограниченно детерминированной, |
|
|
|
Рис. 3.23 |
|
||||||
так как её информационное дерево |
|
|
|
|
|
|
|||||
T f имеет ровно два класса эквивалентности. |
|
|
|
|
|||||||
Следующее утверждение устанавливает связь между понятиями о.д.- функции и конечного автомата.
Теорема. Ограниченно детерминированные функции f : A∞ → B∞ и только они являются автоматными, т.е. реализуются некоторым конечным автоматом. При этом A является входным алфавитом автомата, а B − выходным.
Доказательство. Пусть f : A∞ → B∞ − ограниченно детерминированная функция. Тогда множество вершин информационного дерева T f имеет лишь конечное число ~-классов.
Обозначим классы через q0 , q1 ,..., qn−1 и пометим этими буквами вершины дерева T f , причём корень пометим символом q0 . Нарисуем
n кружочков (см. рис. 3.24)
Если в информационном дереве есть ребро, то соединим кружочки
q0 |
q1 ... qn-1 |
|
Рис. 3.24 |
qi и |
q j |
стрелкой (см. рис. 3.25.), помеченной парой |
(a, b), |
где |
a A − буква алфавита A, соответствующая |
данному ребру информационного дерева. Мы получим (см.
рис. 3.26):
Проделав такую процедуру со всеми возможными
(a,b)
 qi
qi
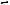




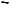
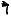
 qj
qj

Рис. 3.26
qj
 b
b

 qi
qi
Рис. 3.25
парами кружочков, мы получим диаграмму Мура некоторого конечного автомата. Ясно, что этот автомат реализует функцию f .
Наоборот, пусть задан конечный автомат V = ( A,Q, B,ϕ,ψ) с начальным состоянием q0 и T f − соответствующее информационное дерево. Пометим корень этого дерева символом q0 . Далее, если v − вершина дерева T f , то существует единственная ветвь, связывающая корень с этой вершиной. Пусть a(1)a(2)...a(k) − слово, определяющее эту ветвь. Пометим вершину v буквой q = ϕ(q0 , a(1)a(2)...a(k)). Таким образом будут помечены все вершины дерева T f . Легко видеть,
что вершины, помеченные одной и той же буквой, являются эквивалентными друг другу. Следовательно, функция f является ограниченно детерминированной. Теорема доказана.

Замечание. Всякая детерминированная, но не ограниченно детерминированная функция может быть реализована с помощью “бесконечного автомата”, т.е. “автомата” с бесконечным множеством
состояний Q.
Пример. Пусть A = B ={0, 1} и f : A∞ → B∞ − функция, определяемая равенством b(i) = a(1) + a(2) +... + a(i) (эта функция была рассмотрена перед теоремой). Ранее мы видели, что функция f в этом примере является ограниченно детерминированной, так как дерево T f имеет два класса эквивалентности. Обозначив эти классы через q0
и q1, получим диаграмму Мура автомата (см. рис. 3.27), реализующего эту функцию.
(0,0)
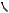



 q0
q0

(1,1) 







 q1
q1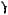



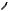 (1,0)
(1,0) 



(0,1)
Рис. 3.27
“Физический смысл” состояний q0 , q1 заключается в следующем.
Нахождение автомата в состоянии q0 означает, что предыдущая сумма a(1) + a(2) +...+ a(i −1) была равна 0, и потому b(i) = a(i); состояние q1 будет в случае, когда a(1) + a(2) +...+ a(i −1) =1, в этом случае b(i) = a(i) +1. Таким образом автомат “запоминает”
необходимую для дальнейшего “предысторию” последовательности a(1), a(2),...
Типовые задачи
Пример 1. Выяснить, какие из следующих функций |
f : A∞ → B∞ |
|||
являются детерминированными: |
|
|
||
|
|
f |
|
|
а) A = B ={0, 1}, a(1)a(2)a(3)... →a(1)a(1)a(2)a(3)a(4)...; |
||||
б) A = B = |
{0, 1}, |
|
f |
|
a(1)a(2)a(3)... →a(2)a(3)a(4)...; |
||||
в) A = B = |
{0, 1}, |
|
f |
|
a(1)a(2)a(3)... →0a(2)0a(4)0a(6)...; |
||||
г) A = B ={0, 1}, |
|
|
|
|
|
|
1 1 1. .. , если a(i) = 0 для всех i, |
||
|
f (a(1)a(2)a(3)...) = |
|
|
|
|
|
a(1)a(2)a(3) . .. в противном случае. |
||
Решение. а) Функция f является детерминированной, так как |
||||
b(i) = a(i −1) при i ≥ 2 − не зависит от a(i +1), a(i + 2), ... |
||||
б) Функция |
f не является детерминированной, так как b(1) зависит от |
|||
a(2), которое неизвестно в момент времени t =1. |
|
|||
в) Функция |
f детерминированная, так как |
|
||
|
|
0, еслиi нечётно, |
−не зависит от |
a(i +1), a(i + 2), ... |
b(i) = |
|
|||
|
a(i), еслиi чётно |
|
|
|
г) Функция |
f детерминированной не является, так как выходная |
|||
последовательность b(1)b(2)b(3)... определится только тогда, когда будут известны a(i) для всех i. Другое объяснение:
0 0 0 111...1... f → 0 0 0 111...,
00 0 0 0 0 ... 0 ... f →111111...,
аэто противоречит определению детерминированности.
Пример 2. Выяснить, какие из следующих функций f : A∞ → B∞ являются ограниченно детерминированными:
а) A = B ={0, 1}, a(1)a(2)a(3)... f → 0 a(1)a(2)a(3) ...;
|
b, |
если a(1) = b, |
б) |
|
если a(1) = c, при i ≥ 2; |
A = B ={a,b, c}, b(1) = a(1), b(i) = c, |
||
|
|
|
|
a(i), если a(1) = a |
|
в) |
A = B ={0, 1}, |
|
f : a(1)a(2)a(3) ... → a(1)a(1)a(2)a(2)a(3)a(3) ...
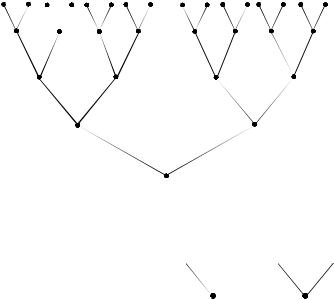
Решение. а) Построим информационное дерево T f , соответствующее
функции f |
: |
|
|
|
|
|
|
|
|
|
|
|
. . . . . . . . . . . . . . . . . . . . . . |
||||||||||||
0 |
0 |
1 |
1 0 |
0 1 |
1 |
0 |
|
0 1 |
1 0 |
0 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
|
0 |
0 |
|
1 |
|
1 |
|
|
0 |
|
0 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Рис. 3.28 |
|
|
|
|
|
|
|
Очевидно, вершины вида, изображенного на рис. 3.29.а. составляют
один класс эквивалентности, а |
|
|
|
|
вершины другого вида (см. рис. |
|
|
|
|
3.29б) – другой класс. Так как |
0 |
0 |
1 |
1 |
получилось конечное число |
|
|
|
|
классов (два класса), то функция |
|
а) |
|
б) |
f ограниченно |
|
Рис. 3.29. |
|
|
детерминирована. |
|
|
||
|
|
|
|
|
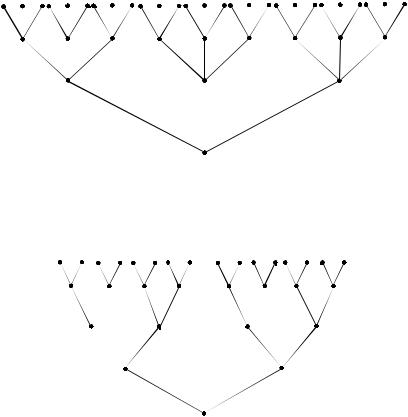
б) Информационное дерево данной функции имеет вид (см. рис.
3.30).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a b |
c a b |
c a b |
c b b |
b b b |
b b b |
b c c |
c c c |
c c c |
c |
|||
|
a |
b |
c |
|
b |
b |
b |
|
c |
c |
c |
|
|
|
|
|
a |
b |
|
c |
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.30
Множество вершин разбивается на 4 класса эквивалентности, поэтому функция f ограниченно детерминирована.
в) Информационное дерево данной функции имеет вид
. . . . . . . . . . . . . . . . . . . . . . .
0 |
0 |
0 |
0 1 |
1 1 |
1 |
0 |
0 0 |
0 1 |
1 |
1 |
1 |
α4 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
|
1 |
|
|
|
|
||||||||
|
α3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
1 |
1 |
|
|
|
|
|
|
α2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
α1 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.31 |
|
|
|
|
||
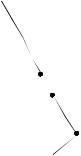
Докажем, что вершины α1, α2 , α3 , ... |
не эквивалентны друг другу. |
||||||||||
Действительно, дерево с корнем αi |
имеет ветвь (см. рис. 3.32) (“1” на |
||||||||||
i -м и (i +1) -м месте и “0” на остальных местах). Значит, деревья |
|||||||||||
T f (α1 ), T f |
(α2 ), ... отличаются друг от друга. Следовательно, имеется |
||||||||||
..

 0
0

 0
0

 1
1

 1
1
... 0

 0
0
αι. 
 0
0
Рис. 3.32
бесконечно много классов эквивалентности вершин дерева T f . Это
означает, что функция f не является
ограниченно детерминированной (хотя является, разумеется, детерминированной).
Можно дать интуитивное объяснение тому факту, что функция f данного
примера не является ограниченно детерминированной. Действительно, для того, чтобы сформировать b(2n), надо
помнить a(n), и с ростом n объём
информации, которую нужно помнить, растёт неограниченно. Поэтому функция f не может быть реализована автоматом с конечным числом
состояний.
Этот пример позволит сделать ещё одно важное замечание. Замечание. Ранее было доказано (см. п. 3.5), что конечный автомат переводит всякую периодическую последовательность в периодическую. Оказывается, что обратное утверждение неверно. Существует детерминированная функция, переводящая всякую периодическую последовательность в периодическую, но не являющаяся ограниченно детерминированной. Примером может служить функция из предыдущей задачи:
f : a(1)a(2)a(3) ... → a(1)a(1)a(2)a(2)a(3)a(3) ...
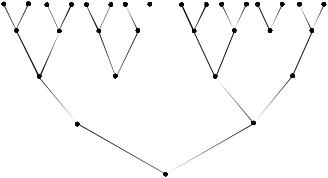
Пример 3. На рисунке 3.33 изображён фрагмент информационного дерева некоторой о.д.-функции. Каково наименьшее возможное число классов эквивалентности вершин этого дерева?
Решение. Понятно, что α и β, а также α и γ лежат в разных ~-
классах. Кроме того, рассматривая ветви длины 3, можно заметить, что β ~/ γ. Рассмотрение ветвей длины 2 показывает, что α ~/ η. Возможно
попадание в один класс эквивалентности вершин α и δ, а также µ и β (или µ и γ ). Таким образом, наименьшее число классов
эквивалентности равно 4. Один из вариантов разбиения на классы эквивалентности следующий: {α,δ,...}, {β, µ,...}, {η,...}, {γ ,...}.
. . . . . . . . . . . . .
1 |
|
|
0 |
|
0 |
1 |
0 |
1 |
1 |
δ |
|
ε |
η |
µ |
0 |
0 |
|
1 |
0 |
β |
γ |
|
0 1
α

Рис. 3.33
Задачи для самостоятельного решения
1. |
Выяснить, какие из следующих функций |
f : A∞ → B∞ являются |
||
детерминированными: |
|
|
||
а) |
A ={0, 1}, B ={a, b, c}, b(1) = a, |
|
|
|
|
|
|
a, если a(i) = a(i −1) = 0, |
|
|
|
|
|
= a(i −1) =1, |
|
|
b(i) = b, если a(i) |
||
|
|
|
|
≠ a(i −1); |
|
|
|
c, если a(i) |
|
б) |
A = B ={0, 1}, |
f (a(1)a(2)a(3)...) = 0 a(1) 0 a(2) 0 a(3)...; |
||
в) |
A = B ={0, 1}, |
|
|
|
|
|
a(1)a(2)a(3)..., если a(i) = 0 при всех чётных i, |
||
|
f (a(1)a(2)a(3)...) = |
|
|
|
|
|
0 a(2) 0 a(4) 0... в противном случае. |
||
2. |
Выяснить, какие из следующих функций |
f : A∞ → B∞ являются |
||
ограниченно детерминированными: |
|
|
||
а) |
A = B ={a,b, c}, |
f (a(1)a(2)a(3)...) = a b c a(1)a(2)a(3)...; |
||
