
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание
Ответы
1. Указание. H ={h G | x0h = x0}. 3. Группа из 2 элементов.
Глава 4. Алгоритмы и машины Тьюринга
§4.1. О понятии алгоритма. Тезис Чёрча
С алгоритмами решения разных математических задач читатель встречался и раньше. В средней школе давался алгоритм решения
квадратного уравнения ax2 + bx + c = 0 ( a ≠ 0), который можно
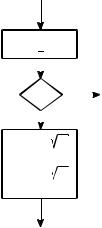
схематически представить в виде Поддаются алгоритмизации многие задачи на построение циркулем и
вычисление
D=b2 4ac
|
|
|
|
|
|
|
да действительных |
||||
|
|
D<0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
корней нет |
|
|
|
|
|
|
|
|||||
x1= |
|
b+ D |
|
|
|||||||
|
|||||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
2a |
|
|
|
|
|
||
x2= |
|
|
b |
|
|
D |
|
|
|||
|
|
|
|
|
|||||||
|
|
|
2a |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
Рис. 4.1
линейкой, дифференцирование элементарных функций, интегрирование рациональных функций и т.д. Такие примеры можно привести не только в математике, но и во многих других науках. Под алгоритмом понимается жёсткое правило, следование которому и выполнение всех
его предписаний приводит к решению задачи. Конечно, эту фразу нельзя считать определением алгоритма. Возникает необходимость дать точное математическое определение алгоритма. Действительно, если мы хотим работать с понятием алгоритма не на интуитивном уровне, а профессионально, применять математический аппарат, то нужно понятие алгоритма уточнить. Кроме того, для доказательства того, что та или иная задача не имеет алгоритма решения, нужно иметь об алгоритме не расплывчатое представление, а чётко знать, что такое алгоритм. Наконец, с уточнением понятия алгоритма можно будет оценивать его сложность, требуемое для реализации машинное время и т.д.
Попытки формализовать понятие алгоритма привели к созданию машины Тьюринга, как некоего воображаемого устройства, реализующего алгоритм. Будем считать, что алгоритм имеет дело со
счётным множеством объектов Ω ={ω0 ,ω1 ,ω2 , ...} и состоит в выборе
одного из них, удовлетворяющего заданным условиям. Таким образом, алгоритм можно отождествить с функцией (вообще говоря, частичной)
f: Ω×... × Ω → Ω. Напомним, что частичной функцией называется
14243
n
“функция” f (x1 , ... , xn ), которая может быть определена не для всех
значений аргументов. Множество Ω мы предполагаем счётным, так как на конечном множестве всегда есть алгоритм решения любой математической задачи (например, она может быть решена полным перебором всех возможных вариантов), а для несчётного множества трудно придумать механическое устройство, преобразующее исходные данные и работающее в дискретном режиме времени (современные вычислительные машины, производящие действия над действительными числами, на самом деле оперируют с их машинными приближениями). Яркими примерами, иллюстрирующими эти рассуждения, являются алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел, алгоритм умножения чисел “в столбик”, деления “уголком”, вычисления п-го простого числа и т.д. – все эти задачи решаются на машинах Тьюринга, которым будет посвящён следующий раздел.
Ещё одним шагом в разрабатываемой теории стало появление рекурсивных функций, как функций, формализующих понятие алгоритма и реализующих интуитивное понятие вычислимости. Вскоре было установлено, что множество рекурсивных функций совпадает с
множеством функций, вычислимых на машинах Тьюринга. Появлявшиеся затем новые понятия, претендующие на объяснение понятия алгоритма, оказывались эквивалентными функциям, вычислимым на машинах Тьюринга, а значит, и рекурсивным функциям. Итогом развернувшейся дискуссии о том, что такое алгоритм, стало утверждение, называемое сейчас тезисом Чёрча. Тезис Чёрча. Понятие алгоритма, или вычислимости некоторым механическим устройством, совпадает с понятием вычислимости на машинах Тьюринга (а значит, с понятием рекурсивной функции). Это утверждение нельзя считать математической теоремой. Это есть некоторый естественнонаучный тезис, принятый большинством исследователей.
§4.2. Машина Тьюринга
Машина Тьюринга так же, как и конечный автомат, является дискретным устройством преобразования информации. Приведём её точное определение, а затем интерпретацию её работы. Определение. Машиной Тьюринга называется частичное отображение
{0,1, ... , n −1}×{0,1} M →{0,1, ... , n −1}×{Λ, Π}×{0,1}.
Здесь Λ, Π обозначает “лево”, “право”. Тот факт, что отображение M
частичное, означает, что M может быть определено не для всех наборов аргументов. Машина Тьюринга M работает с бесконечной в обе стороны лентой, разбитой на ячейки, в каждой из которых написан
.... |
|
0 |
|
0 |
|
1 |
|
0 |
|
1 |
|
1 |
|
1 |
|
0 |
|
0 |
|
1 |
|
1 |
|
.... |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.2
один из символов 0, 1. Считывающая головка машины обозревает в каждый момент времени одну из ячеек и за один такт, сменяющий два последовательных момента времени, может перемещаться влево или вправо. Машина Тьюринга в каждый момент времени находится в
одном из состояний q0 , q1 , ... , qn−1 , а в следующий момент времени
переходит в другое состояние или остаётся в том же. Кроме того, машина может изменять символ, стоящий в обозреваемой ячейке. Все эти преобразования – изменение состояния, информация на ленте, направление движения полностью определяются отображением M. А именно, если M (i,ε) = ( j, Λ,η), то в случае, когда машина находится в
состоянии qi , а на обозреваемой в данный момент ячейке написан символ ε, машина должна записать в эту ячейку η вместо ε, перейти в состояние q j и сдвинуться на одну ячейку влево. В случае, когда M (i,ε) = ( j, Π,η), те же действия будут сопровождаться сдвигом
вправо. Например, равенство M (2,1) = (1, Π,1) означает, что, находясь в состоянии q2 и обозревая ячейку, в которой написан символ 1, машина должна сохранить в этой ячейке символ 1, сдвинуться вправо и перейти в состояние q1. Если же M (i,ε) не определено, то машина, находясь в состоянии qi и обозревая ячейку с символом ε, прекращает свою
работу, не изменяя своего состояния, информации на ленте и никуда не сдвигаясь.
Замечания. 1. Существуют различные модификации машины Тьюринга (машина Поста, машина Минского и т.д.). Некоторые модификации предусматривают на ленте не символы 0 или 1, а буквы некоторого
конечного алфавита A ={a1 , ... , am }. В некоторых определениях
разрешается не только сдвиг головки машины влево или вправо, но и оставление на прежней позиции. Однако, различные модификации машины Тьюринга эквивалентны между собой в том смысле, что классы функций, вычислимых на этих машинах, совпадают.
2. Понятно, что никакое физическое устройство не может иметь бесконечной ленты. Поэтому лучше мыслить себе ленту машины Тьюринга как потенциально бесконечную, т.е. как конечную, к которой при необходимости можно “подклеивать” с одной и с другой стороны куски сколько угодно раз.
Определение машины Тьюринга, данное в начале раздела, неудобно для использования. Более удобным будет запись программы, которая заключает в себе всю информацию о работе машины (таким образом, задания машины с помощью отображения и с помощью программы эквивалентны между собой). Опишем составление программы. Для
каждого равенства вида M (i,ε) = ( j, Η,η), где i, j − номера состояний, Η − направление движения, а ε,η − символы на ленте, запишем строку qiε q j Ηη и назовём её командой. Совокупность всех команд – это и есть программа. Если M (qi ,ε) не определено, то в программе нет ни одной команды, начинающейся с qiε. Кроме того, для любых i,ε в программе есть не более одной команды, начинающейся с qiε.
Пример. Построим машину Тьюринга, которая, имея на ленте два массива из единиц, разделённые нулями, заполняет эти нули единицами и останавливается у последней единицы второго массива.
... 0 1 1 100011110... →... 01111111111 0... |
|
↑ |
↑ |
qo |
q |
|
|
Алгоритм действий можно записать словами:
1-й шаг: пройти первый массив единиц, найти массив из нулей, идущий после него и заменить первый нуль единицей; 2-й шаг: идти через массив нулей, заменяя их единицами, до тех пор, пока не появится второй массив единиц;
3-й шаг: пройти второй массив единиц и остановиться в его конце. Машина Тьюринга, реализующая этот алгоритм, имеет следующую программу:
q0 1 q0 Π1 |
1-й шаг |
||
q0 0 q1Π1 |
|||
|
|||
q1 0 |
q1Π1 |
2-й шаг |
|
q11 q2Π1 |
|||
|
|||
q01 |
q2Π1 |
3-й шаг |
|
q2 0 |
q3Λ0 |
||
|
|||
Ввиду наличия у машины Тьюринга бесконечной ленты её вычислительные возможности значительно превосходят возможности конечного автомата. В частности, так как автомат имеет конечную память, то выходная последовательность его всегда периодическая, если входная периодична (см. п.3.5). В противоположность этому нетрудно
придумать машину Тьюринга, которая, начиная работать на пустой ленте (т.е. на ленте, во всех ячейках которой записаны нули), будет формировать последовательность ...0101101110111101111101...
(массивы из единиц имеют длины 1, 2, 3, ...), а эта последовательность периодической не является.
Будем называть в этой главе натуральными числами целые неотрицательные числа, т.е. разрешим числу 0 называться натуральным числом. Таким образом, N ={0, 1, 2, ...} − множество натуральных
чисел. Как на ленте обозначить натуральное число x ? Один из способов (и мы будем его использовать) состоит в том, что число x кодируется последовательностью из x +1 единиц (именно x +1, а не x, чтобы не путать число 0 с отсутствием информации). Такую
информацию на ленте будем обозначать [x]. Например,
[3] =...0111100... Упорядоченный набор (x1, x2 ,..., xn ) натуральных чисел будем кодировать так: 0[x1 ]0[x2 ]0...[xn ]0. Определим теперь, что означает вычислимость функции f машиной Тьюринга M .
Определение. Машина Тьюринга M вычисляет функцию
f (x1,..., xn ), если для любого набора (x1, x2 ,..., xn ) натуральных чисел машина M , находясь в состоянии q0 и обозревая крайнюю левую единицу в ...0[x1 ]0[x2 ]0...[xn ]0..., останавливается в том и только том случае, когда значение f (x1 ,..., xn ) определено, и в конце работы на ленте должно быть записано ...0[ f (x1 ,..., xn )] 0..., а
считывающая головка машины должна стоять напротив крайней левой единицы.
Таким образом, если, например, |
f (2,3) =1, то мы должны иметь |
...0 1 11011110... →...0 110... |
|
↑ |
↑ |
qo |
qi |
а если f (2,3) не существует, то машина, запущенная на ленте
...0[2]0[3]0..., должна работать бесконечно долго (при условии, что начальное состояние q0 , а обозреваемая в начальный момент времени ячейка – крайняя левая единица.
Если информация на ленте не имеет вид ...0[x1]0[x2 ]0...[xn ]0..., или начальное состояние не q0 , или обозреваемая ячейка – не крайняя
левая единица, то поведение машины может быть каким угодно. Пример. Машина, заданная следующей программой, вычисляет функцию f (x, y) = x + y.
q01 q0Π1 |
q1 0 q2Λ0 |
q41 q4Λ1 |
q0 0 q1Π1 |
q21 q3Λ0 |
q4 0 q5Π0 |
q11 q1Π1 |
q31 q4 Λ0 |
|
Машина Тьюринга была придумана Аланом Тьюрингом и описана в его статье в 1936 г. Конечно, она уступает современным вычислительным машинам в удобстве использования для решения конкретных задач. Тем не менее она сыграла большую роль в создании вычислительной техники. К настоящему времени она сохранила своё теоретическое значение для решения вопроса об алгоритмической разрешимости задач.
Примеры решения задач
Пример 1. Построить машину Тьюринга, вычисляющую функцию:
а) f (x) ≡ 0; б) f (x, y) = max(x, y).
Решение. а) Фактически надо, имея следующую ситуацию на ленте
...0 111...10 ..., уничтожить все единицы, кроме первой. Пусть q1 −
↑
qo
состояние, в котором машина ищет крайнюю правую единицу, попутно стирая все единицы, начиная со второй, q2 − движение влево до
оставшейся единицы. Программа машины выглядит так: q01 q1Π1 q11 q1Π0 q1 0 q2 Λ0 q2 0 q2 Λ0.
б) Словесно алгоритм вычисления функции max(x, y) можно
сформулировать так: будем заменять в массивах из единиц последние единицы нулями до тех пор, пока в одном или обоих массивах не останется ровно одна единица; затем заменим все нули, стоящие между массивами из единиц, единицами; наконец, удалим две последние единицы.

...011101111100... → ...010 0 01110 0 00... → ...011111110000... → |
|||||
|
•• |
•• |
• • |
• • |
123 |
|
|
||||
→ ...011111000000... |
|
|
|||
Программа машины выглядит так: |
|
|
|||
|
q01 q1Π1 |
|
|
|
|
|
q11 q2Π1 |
находим последнюю единицу в первом массиве из |
|||
|
q21 q2Π1 |
||||
|
единиц и стираем её, если она не единственная |
||||
|
q2 0 |
q3Λ0 |
|
|
|
|
q31 q4Π0 |
|
|
|
|
|
q4 0 q4Π0 |
|
|
|
|
|
q41 q5Π1 |
|
|
|
|
|
q51 q6Π1 |
то же делаем со вторым массивом из единиц |
|||
|
q61 q6Π1 |
||||
|
|
|
|
||
|
q6 0 |
q7 Λ0 |
|
|
|
q71 q8Λ0
q81 q8Λ1 q8 0 q9 Λ0
q9 0 q9 Λ0 возвращаемся к крайней левой единице
q91 q10 Λ1 q101 q10Λ1 q10 0 q0Π1
q1 0 q11Π1 q11 0 q11Π1
q111 q12Π1 заменяем промежуточные нули единицами
q121 q12Π1 q12 0 q13Λ0
q5 0 |
q14 Λ0 |
|
|
q14 |
1 |
q15Λ1 |
|
q15 0 q15Λ1 |
|
||
q151 |
q12Π1 |
стираем последние две единицы и останавливаемся |
|
q |
1 |
q Λ0 |
у крайней левой единицы |
13 |
|
16 |
|
q161 q17 Λ0 |
|
||
q17 |
1 |
q17 Λ1 |
|
q17 |
0 q18Π0 |
|
|
2. Определить, какую функцию f (x) вычисляет машина Тьюринга, заданная следующей программой:
q01 q0Π1 |
q11 q2 Λ0 |
q11 q3Λ1 |
q0 0 q1Λ0 |
q2 0 q2 Λ0 |
q3 0 q4Π0 |
Решение. Если внимательно проследить за работой машины, то можно заметить, что если вначале на ленте была только одна единица, то
машина, перейдя в состояние q1, её сотрёт и затем будет работать
бесконечно долго, а если на ленте более одной единицы, то она сотрёт последнюю из них и остановится около первой. Поэтому
|
x −1, |
если x ≥1, |
|
|
f (x) = |
|
|
|
не определено, если x = 0. |
|
|
Задачи для самостоятельного |
|||
|
решения |
|
|
1. Построить машину Тьюринга, реализующую функцию: |
|
||
а) f (x) = x +1; б) f (x, y) = x. |
|
|
|
q11 q1Π0 |
q31 q3Λ1 |
|
|
q1 0 q2Λ0 |
q3 0 q4Π0 |
|
|
2. Определить, какие функции вычисляют следующие машины |
|||
Тьюринга: |
|
|
|
а) |
|
|
|
q01 q0Π1 |
q3 0 q3Λ0 |
(функция двух переменных) |
|
q11 q2Π1 |
q31 q4 Λ1 |
||
q21 q2Π0 |
q41 q5Λ1 |
|
|
q2 0 q3Λ0 |
q1 0 q5Λ0 |
|
|
б) |
|
|
|
q01 q1Π1 |
q3 0 q4Π0 |
(функция |
одного |
q11 q1Π1 |
q21 q3Λ1 |
||
q1 0 q2 Λ0 |
q1 0 q4 Λ0 |
переменного) |
|
|
|
||
