
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание

|
|
f |
|
б) A = B ={0, 1}, a(1)a(2)a(3)... →0 a(1) 0 a(2) 0 a(3)...; |
|||
в) A = B ={a,b, c}, |
b(i) = |
a(i), если j ≤ i |
a( j) ≠ c, |
|
a( j) = c. |
||
|
|
c, если j ≤ i |
|
3. Определить количество классов эквивалентности множества вершин дерева T f следующих функций:
а) A ={0, 1}, B ={0, 1, 2}, b(i) = a(1) + a(2) + ... + a(i) (mod 3);
б) |
A = B ={0, 1}, f (a(1)a(2)a(3)...) = 0 0 a(1)a(2)a(3)...; |
|
в) |
A ={a,b, c}, B ={0, 1}, b(i) = |
0, еслиi =1 или a(i) ≠ a(i −1), |
|
||
|
|
1 в противном случае. |
Ответы
1. а) Детерминированная; б) детерминированная; в) недетерминированная. 2. а) Является; б) не является; в) является. 3. а)
3; б) 4; в) 4.
§3.8. Синтез автоматов
Под синтезом автоматов мы понимаем построение автоматов, удовлетворяющих заданному свойству или выполняющий заданные функции. Ранее в п.3.1 был построен элемент задержки, который сдвигает входную последовательность на 1 такт: b(i) = a(i −1) при
i ≥ 2 (см. рис. 3.34).
Z
Рис. 3.34
Соединяя последовательно два элемента задержки, мы получим сдвиг на 2 такта: b(i) = a(i − 2) при i ≥ 3 (см. рис.3.35).
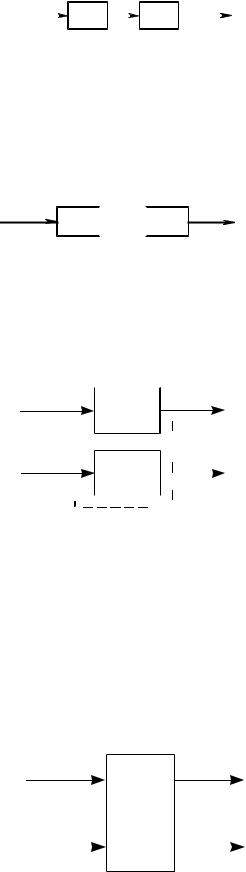
a(t) |
Z |
|
|
Z |
b(t) |
|
|
|
|
||
|
|
Рис. 3.35 |
|
||
Автоматы V1 = ( A1,Q1, B1,ϕ1,ψ1 ) и V2 = ( A2 , Q2 , B2 ,ϕ2 ,ψ2 ) можно соединять последовательно в случае, если B1 A2 (см. рис. 3.36). При этом получается автомат V = ( A,Q, B,ϕ,ψ), у которого
A = A1, B = B2 , Q = Q1 ×Q2 ,
ϕ((q1, q2 ), a) = (ϕ1 (a, q1 ), ϕ2 (ψ1 (a, q1 ), q2 )),
ψ((q1, q2 ), a) =ψ2 (ϕ1 (a, q1 ), q2 ).
V1 

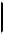 V2
V2
Рис. 3.36
Параллельное соединение автоматов приводит к появлению автомата
V= ( A1 × A2 , Q1 ×Q2 , B1 × B2 , ϕ,ψ) (см. рис. 3.37), где
ϕ((q1, q2 ), (a1, a2 )) = (ϕ1 (q1, a1 ),ϕ2 (q2 , a2 )),
ψ((q1, q2 ),(a1, a2 )) = (ψ1 (q1, a1 ),ψ2 (q2 , a2 )).
Пусть V = ( A,Q, B,ϕ,ψ) − конечный автомат. Если
A ={a , a |
|
,..., a |
|
|
} и m ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
символ a можно |
||||
|
m |
|
|
2k |
, |
то входной |
|
|||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b(1)b(2)... |
|||
|
|
|
|
|
|
a(1)a(2)... |
|
|
|
|
|
|
|
V1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k, а именно: |
||||||||
закодировать двоичной |
|
|
последовательностью |
|
|
длины |
||||||||||||||||||||
a |
→ 00...0, |
a |
|
|
→ 00...1, |
|
|
a |
|
→ 00...10 и т.д. Аналогично, если |
||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
1 |
123 |
|
2 |
|
|
123 |
|
|
|
|
3 |
123 |
|
|
|
|
||||||||||
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
b(1)b(2)... |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
a(1)a(2)... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
B ={b , ... ,b } |
|
и |
n ≤ 2l , |
|
то выходные символы b B могут быть |
|||||||||||||||||||||
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
V2 |
|
|
|
|||||||
представлены двоичными |
|
последовательностями длины l. Автомат V , |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||
(см. рис. 3.38) таким образом, становится ус тройством, перерабатывающим двоичную информациюРис. 3.37 :
тройством, перерабатывающим двоичную информациюРис. 3.37 :
x1(t) y1(t)
. . . . |
V .... |
|
xk(t) |
|
yl(t) |
Рис. 3.38

Выходы y j (t) представляют собой булевы функции от входов
 &
&
Z |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||
|
|
|
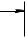
Рис. 3.39 |
||
x1 (i), ... , xk (i), где i = t, t −1, ... Эти функции можно реализовать с
помощью схем, содержащих стандартные булевы элементы и элемент задержки (см. рис. 3.39):
Пример. Рассмотрим устройство, осуществляющее сложение двух двоичных последовательностей с переносом разряда. Например,
x(t) |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
. . . |
y(t) |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
b(t) |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
. . . |
|
x(t) + y(t), |
если не было переполнения, |
Таким образом, b(t) = |
|
|
|
x(t) + y(t) +1 в противном случае. |
|
1, |
если есть переполнение, |
|
Положим u(t) = |
если нет. |
Тогда |
0, |
|
|
b(t) = x(t) + y(t) + u(t −1), u(t) = 0, если среди чисел x(t), y(t), u(t −1) не более одного равны 1, u(t) =1 в противном случае. Нетрудно видеть, что u(t) = x(t) y(t) + (x(t) + y(t))u(t −1). Теперь мы можем изобразить схему устройства (см. рис. 3.40):
x(t) |
& |
|
|
|
|
||
|
|
|
|
y(t) |
& |
|
|
|
|
||
|
Z |
|
|
|
|
b(t) |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.40 |
|
Типовые задачи
Пример 1. Дан алфавит A ={a,b, c}. Построить автомат,
отыскивающий во входной последовательности подслово abc и заменяющий после этого все символы символом . Например,
ababbca cbabcabba... → ababbca cbabc ...
Решение. Пусть q0 обозначает начальное состояние, qa − состояние,
в которое автомат перейдёт, получив на входе символ a, qb − символ b (но не после a), qc − символ c (но не после ab). Далее, пусть q′− состояние ожидания символа c, если уже есть ab , q′′ − есть
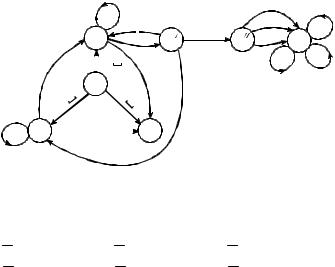
abc , Наконец, пусть q − финальное состояние. Изобразим теперь диаграмму Мура искомого автомата (см. рис. 3.41).
b,b
|
b |
, |
|
a |
|
a,a |
a,b |
||
qa |
|||
q |
|||
|
a, |
b,a |
|
|
|||
|
c,a |
||
q0 |
|||
c |
|||
|
|
||
, |
|
, |
|
b |
|
||
|
c,c |
|
|
c,b |
a,c |
a,* |
|
q b,c |
|||
|
q* |
||
|
c,* |
b,* |
qb |
c,b |
|
||
|
|
|||
qc b,b |
||||
|
||||
Рис. 3.41
Пример 2. Существует ли конечный автомат V с алфавитами
A = B ={0, 1} такой, что: |
|
|
|||
а) ψ |
(q0 ,011) =101, |
ψ |
(q0 ,110) = 000, |
ψ |
(q0 ,010) =111? |
б) ψ |
(q0 ,011) =101, |
ψ |
(q0 ,110) = 000, |
ψ |
(q0 ,010) =100? |
Решение. а) Такого автомата не существует: действительно, у входных слов 011 и 010 совпадают первые две буквы, а выходные слова 101 и 111 этим свойством не обладают. Другими словами, функцию
ψ (q0 , x) нельзя продолжить до детерминированной функции f : A∞ → B∞.
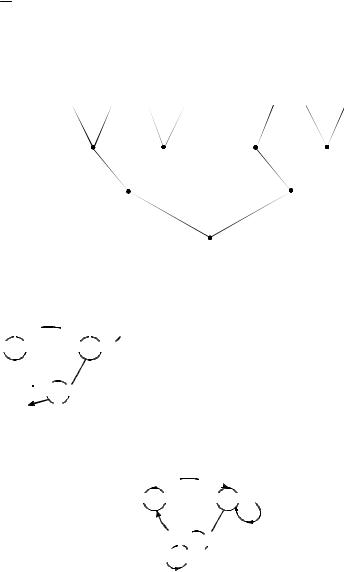
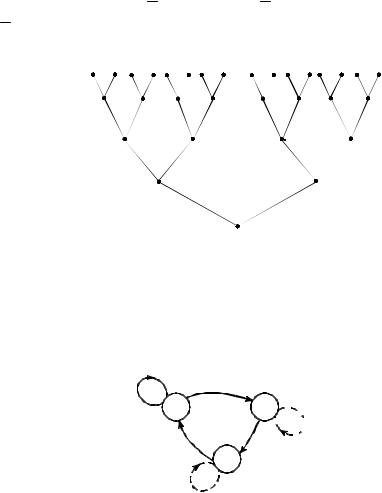
б) Условие детерминированности здесь выполнено. Докажем, что автомат, удовлетворяющий данным условиям, существует. Построим фрагмент информационного дерева:
0 |
1 |
|
|
0 |
|
γ |
η |
0? |
ε |
|
0 |
1? |
0 |
|
β |
1 |
0 |
δ |
|
|
α |
|
|
|
|
Рис. 3.42 |
|
|
|
Вершины α и γ не эквивалентны. Если ребро δη будет помечено
0,1



 1,0
1,0



 q0
q0





 q1
q1


 0,1
0,1
0, |
1,0 |
0 |

 q2
q2
 1,1
1,1 

Рис. 3.43
символом 0, то δ ~/ α и δ ~/ γ; если же
его пометить символом 1, то всё равно
α ~/ δ. Пусть q0 ={α, ...},
q1 ={β,δ,...}, q2 ={ε,γ , ...}. Получим
(см. рис. 3.43):
Замыкая произвольным образом повисшие стрелки этой диаграммы, получим диаграмму Мура автомата (см. рис. 3.44):
0,1


 1,0
1,0


 q0
q0






 q1
q1



0 |
1,0 |
0,1 |
0 |
|
|
, |
|
|


 q2
q2
 1,1
1,1




Рис. 3.44
Пример 3. Построить автомат с наименьшим числом состояний, для
которого A = B ={0, 1}, ψ |
(q0 ,010) =110, |
ψ |
(q0 ,0111) =1110, |
||||
ψ |
(q0 ,11) = 00. |
|
|
|
|
||
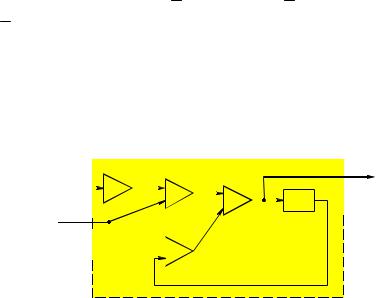
Решение. Построим информационное дерево: |
|
||||||
|
|
|
|
0 |
|
|
|
0 |
δ |
|
|
|
|||
1 |
|
|
|
||||
|
|
|
|
γ |
|
|
|
1 |
|
|
|
0 |
|||
|
|
β |
1 |
0 |
ε |
||
|
|
|
|||||
α
Рис. 3.45
Очевидно, α ~/ β, β ~/ γ , α ~/ γ. Значит, количество классов эквивалентности информационного дерева (т.е. количество состояний автомата) не меньше 3. Полагаем q0 ={α,ε,δ, ...}, q1 = {β,...},
q2 = {γ , ...} и получаем диаграмму Мура искомого автомата (см.
рис.3.46):
0,1 |
|
q1 |
|
0,1 q0 |
|
|
|
1 |
|
|
1 |
|
, |
||
1 |
|
1 |
|
, |
q2 |
|
|
0,0 |
|
|
|
|
|
|
|
 0,0
0,0
Рис. 3.46
Пунктиром обозначены стрелки, добавленные для обеспечения полноты диаграммы. Эти стрелки можно направить в другие кружочки.
Задачи для самостоятельного решения
1. Построить автомат с входным и выходным алфавитами A ={a,b, c} и B ={_, a,b, c, }, который отыскивает во входной
последовательности идущие подряд более одного раза буквы a и заменяет последнюю из них символом . Символ _ зарезервирован здесь для начала последовательности. Пример:
abbcaabcacaaabc... → _ abbca bcacaa bc...
2. Построить диаграмму Мура автомата с A = B ={0, 1}, который во
входной последовательности заменяет символы, стоящие на чётных местах, на противоположные. Например,
01100101001110... → 00110000011011...
3. Построить таблицу автомата с наименьшим числом состояний, удовлетворяющий условиям: ψ (q0 ,011) =111, ψ (q0 ,1011) =1101,
ψ (q0 ,11) =10.
4. Автомат V с A = B ={0, 1} работает по схеме, показанной на рисунке 3.47. При этом считается, что u(0) = 0.
а) Выразить u(t) через x(t), y(t), u(t −1).
б) Найти первые 3 символа в выходной последовательности, если x(1)x(2)x(3) ... =10 0 ..., y(1) y(2) y(3) ... = 011 ...
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(t) |
|
|
|
|
¬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
Z |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||


Рис. 3.47

|
|
|
|
|
|
|
|
|
Ответы |
|
|
||||
1. См. рис. 3.48. 2. См. рис. 3.49. |
|
|
|
|
|
|
|||||||||
|
c |
|
|
c,a |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
a |
|
|
|
|
|
|
|
|
||
|
|
c |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qc |
|
|
|
b, |
|
|
|
qa |
|
a,a |
|
qa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
c,c |
|
|
c |
|
b |
|
|
|
|
|
|
0,0 |
|
||
|
|
|
, |
|
|
|
|
|
|
|
|
||||
|
b |
b |
a |
|
|
a |
, |
|
|
|
|
|
|||
|
, |
|
|
|
|
|
|
|
|||||||
|
c |
|
|
, |
b* |
|
|
|
1,1 |
|
|||||
|
qb |
|
b |
|
|
|
|
q1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||
|
|
b,b |
|
|
|
|
|
|
|
|
q |
0,1 |
|||
|
|
|
|
|
|
c,* |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
|
||
|
|
|
|
Рис. 3.48 |
|
|
|
|
|
|
Рис. 3.49 |
|
|||
3. См. табл. 3. |
|
. (ответ неоднозначен). |
|
|
|
|
|||||||||
|
|
|
|
|
|
q0 |
|
q1 |
|
q2 |
Таблq. |
33. . |
|
||
|
|
|
|
0 |
q1 |
1 |
|
q3 |
0 |
q3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
1 |
q2 |
1 |
|
q0 |
1 |
q0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. а) u(t) = y(t) x(t)u(t −1); б) u(1)u(2)u(3) ... = 011 ... |
|
||||||||||||||
