Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Дискретная математика

Файл:

Литература / Учебник (Кожухов, Прокофьев, Соколова) / discret_mat.pdf

Скачиваний:

588

Добавлен:

16.04.2013

Размер:

2.43 Mб

Скачать

☆

<<< < Предыдущая 12 / 222 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

23. Черный «Бьюик». 24. Третий учащийся изучал логику. 25. Сидоров. 29. а) нет; б) да; в) нет.

§1.2. Функции алгебры логики

Определение. Прямым (декартовым) произведением множеств

~	= A1	× A2	×K× An ) называется
A1 , A2 , K, An (обозначается A
множество всех векторов (a1 , a2 , K, an )			таких, что ai Ai , 1 ≤ i ≤ n .

Если все множества Ai совпадают и равны A , то используют

обозначение An = A × A ×K× A .

1442443

n раз

Основные понятия и факты, связанные с булевым кубом

В дальнейшем в качестве множества Ai будет использоваться множество E2 ={0, 1}.

Определение. Набор (α1 , α2 , K, αn ) , где αi {0, 1}, 1 ≤ i ≤ n ,

называется булевым или двоичным набором (вектором). Элементы набора называют компонентами или координатами. Число n

					~	~ n	.
называют длиной набора. Кратко (α1 , K, αn ) обозначают α						или α	.
	~ n		называют число его координат, равных
Весом (или нормой) набора α			называют число его координат, равных
~ n	n	~	n	n−k
~ n	\|\| = ∑αi . Число ν	~		n−k	называют номером
1, т.е. \|\|α	\|\| = ∑αi . Число ν	(α) = ∑αk 2			называют номером
~	i=1		k =1
~
набора α .

Замечание. Набор (α1 , K, αn ) есть разложение числа ν(σ~) в двоичной системе и находится следующим образом: а) делим ν(σ~) на 2, остаток есть αn частное σ n ; б) делим σ n на 2, остаток есть αn−1 частное σn−1 ; и т. д. до тех пор пока не получим частное, равное 0.

					~ n	длины n
Определение. Множество всех булевых векторов α						длины n
называется n -мерным кубом ( E2n = E2 ×K× E2 ). Сами векторы
					14243
					n раз
называются вершинами n -мерного куба.
Кроме обозначения E2n					для n -мерного куба используют обозначение
B	n	~ n	B	n	называют вершинами куба B	n	.
B		, а наборы α	B		называют вершинами куба B		.

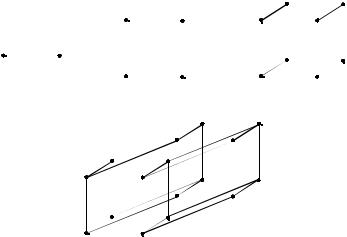
Геометрическая реализация. На рисунке 1.1. изображены проекции, соответственно, 1-мерного, 2-мерного, 3-мерного и 4-мерного кубов на плоскость.

															1,1,0		1,1,1
0		1	1,0						1,1				0,1,0				0,1,1
																1,0,0	0,1,1		1,0,1

			0,0							0,1
	E1
	E1
2								E2					0,0,0		E3			0,0,1
								E2							E3
						2									2
										1,1,1,0					1,1,1,1
						1,0,1,0									1,1,1,1
		0,1,1,0				1,0,1,0								1,0,1,1
						0,1,1,1								1,0,1,1
						0,1,1,1
		0,0,1,0		0,0,1,1							1,1,0,0				1,1,0,1
							1,0,0,0								1,1,0,1
							1,0,0,0
		0,1,0,0											1,0,0,1
							0,1,0,1
		0,0,0,0										E24
		0,0,0,0			0,0,0,1							E24
								Рис. 1.1
Определение. Пусть σi					, σi	2		, K, σi		− фиксированная система чисел
			1			2				k

из 0 и 1 (1 ≤ i1 < i2 <K< ik ≤ n ). Множество всех вершин (α1 , K, αn )

куба Bn таких, что

αi1 =σi1 , αi2 =σi2 , K, αik =σik ,

называется (n − k) -мерной гранью.

Замечание. (n − k) -мерная грань является (n − k) -мерным подкубом

куба Bn .

Определение. Расстоянием (Хемминга) между вершинами α и β

куба B

называется число ρ

= ∑|αi − βi | (т.е. число

(α

, β )

i=1

отличаются друг от друга).

координат, в которых наборы α

и β

куба B

– соседние, если

Определение. Вершины α и

(α,

β )

=1, и противоположные; если ρ(α, β ) = n .

Определение. Говорят, что набор α предшествует набору β

≤ βi для всех i =

(обозначают αp β ), если αi

1, K, n . Если αp

β и

≠ β , то говорят, что набор α

строго предшествует набору β

обозначают α p β . Наборы α и β называют сравнимыми, если либо

αp β

либо β pα .

~ n

) = f (x1 , K, xn )

такая, что

Определение. Функция f (x

f : E2n

→ E2 называется булевой функцией (или функцией алгебры

логики) от n переменных.

Замечание. Булевы функции являются удобными для описания, анализа и синтеза переключательных схем, выходные сигналы которых характеризуются лишь двумя уровнями напряжения: высоким (1) и низким (0). Поэтому в практических приложениях их еще называют

переключательными.

Для задания булевой функции			~ n	) требуется указать ее значения на
			f (x
n	. При	n ≥1		~ n	) можно задать
каждом наборе E2			функцию f (x

таблицей T f (табл. 1.1), называемой таблицей истинности функции,

в которой наборы ~ K выписываются в порядке

σ = (σ1 , , σn )

возрастания их номеров (сверху вниз).

Табл. 1.1.

x1	x2	K	xn−1	xn	~ n	)
x1	x2	K	xn−1	xn	f (x	)
0	0	K	0	0	f (0, 0, K, 0, 0)
0	0	K	1	1	f (0, 0, K, 0, 1)
0	0	K	1	0	f (0, 0, K, 1, 0)
K	K	K	K	K	K

0	1	K	1	1	f (0, 1, K, 1, 1)
1	1	K	1	1	f (1, 1, K, 1, 1)

При стандартном расположении наборов (в соответствии с увеличением

их номера), функцию ~ n можно задавать вектором ее значений f (x )

~ 2n	= (α0 , α1 ,K, α2n −1 )		~
α f	= (α0 , α1 ,K, α2n −1 )		(или α f ), где координата αi равна
	~ n	)	в i -ой строке таблицы ( i = 0,1, K, 2					n	−1 ),
значению функции f (x		)	в i -ой строке таблицы ( i = 0,1, K, 2						−1 ),
	~
т.е. на наборе σi . При этом значение переменной xk i -ой строке
			~
таблицы есть компонента σ k набора σi , которая определяются как
					~
соответствующая k -я цифра в записи числа i =ν(σ ) .
Обозначим P2 (n) − множество всех булевых функций от n
переменных, а P2 − множество всех булевых функций.
Теорема. Число функций в P (n) равно 22 n .
			2
			~ n		) задается вектором
Доказательство. Поскольку функция f (x					) задается вектором
	~		, α2n −1 ) , где αi	{0,1} , 0 ≤ i ≤ 2		n	−1 , то
значений α f = (α0 , α1 ,K			, α2n −1 ) , где αi	{0,1} , 0 ≤ i ≤ 2			−1 , то

различных булевых функций от n переменных столько же, сколько различных 2n -разрядных двоичных векторов, т.е. 22 n .

Фиктивные и существенные переменные

Для сравнения булевых функций от одного количества переменных вводятся следующие понятия.

Определение. Переменная xi для функции f (x1 , K, xn ) называется существенной ( f зависит от xi существенно), если существует такой набор (β1 , K, βi−1 , βi+1 ,K, βn ) , что

f(β1 , K, βi−1 , 0, βi+1 ,K, βn ) ≠ f (β1 , K, βi−1 ,1, βi+1 ,K, βn ) .

Впротивном случае переменная xi – фиктивная, т.е. функция f не

зависит от xi .

Процедура удаления (введения) фиктивных переменных

	Пусть переменная xi для функции									~ n		) – фиктивная. Тогда для ее
	Пусть переменная xi для функции								f (x			) – фиктивная. Тогда для ее
	удаления вычеркиваем все строки таблицы, в которых xi																	=1 и столбец
	переменной xi . В итоге получаем функцию от n −1 переменной.
	Определение. Две функции f1 и								f2 от разного количества
	переменных равны, если одна получается из другой путем удаления или
	введения фиктивных переменных.
					~3	) задана таблицей 1.2. Определить фиктивные
	Пример. Функция f (x					) задана таблицей 1.2. Определить фиктивные
	переменные функции.																		x3 функции
		Решение. Убеждаемся, сначала в том, что переменная																	x3 функции
						~3		)	является				фиктивной.						Удаляя			ее,
				Табл.		f (x		)	является				фиктивной.						Удаляя			ее,
1.2				Табл.											~ 2		)
						получим			функцию						~ 2			(табл.			1.3).
						получим			функцию							f (x		(табл.			1.3).
						Переменная					x	также является фиктивной. В
	x1	x2	x3	~3	)	Переменная					x	также является фиктивной. В
	x1	x2	x3	f (x	)					1		~		3	) = x2 (табл. 1.4).
	0	0	0	1		итоге получаем						~		3
	0	0	0	1		итоге получаем						f (x
	0	0	1	1							Таблл.1.3
	0	1	0	0															Табл. 1.4
	0	1	0	0			x1		x2			~3							Табл. 1.4
	0	1	1	0							f (x		)
	0	1	1	0							f (x		)					x2		~	3	)
																				~	3
	1	0	0	1			0		0			1								f (x
																		0		1
							0		1			0
	1	0	1	1			0		1			0
																		1		0
							1		0			1
	1	1	0	0
	1	1	0	0
							1		1			0
	1	1	1	0			1		1			0

Благодаря введенному понятию конечную совокупность булевых функций можно считать зависящей от одного и того же числа

переменных, являющегося объединением множеств переменных всех функций совокупности.

Функции от одной переменной

	В таблице 1.5 представлены все булевы	Табл. 1.5
	функции одной переменной.	Табл. 1.5
	функции одной переменной.

Функции f0 и f3 называются

соответственно (тождественным) нулем и (тождественной) единицей.

Функция f1 называется

тождественной функцией и обозначается x .

Функция f2 называется отрицанием обозначается x или ¬x и читается «не x ».

x1	f0	f1	f2	f3
0	0	0	1	1
1	0	1	0	1
(или		инверсией) x ,

Функции от двух переменных

В таблице 1.6 представлены все булевы функции от двух переменных.

Табл. 1.6

x1	x2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Функция f1 называется конъюнкцией x1 и x2 , обозначается x1 & x2 или x1 x2 , или x1 x2 , и часто читается « x1 и x2 ».

Функция f6 называется суммой по модулю 2 x1 и x2 , обозначается x1 x2 или x1 + x2 , и часто читается « x1 плюс x2 ».

Функция f7 называется дизъюнкцией x1 и x2 , обозначается x1 x2 ,

и часто читается « x1 или x2 ».
Функция f8 называется стрелкой Пирса x1 и	x2 ,	обозначается
x1 ↓ x2 , и часто читается «ни x1 , ни x2 » или «ни	x1	и ни x2 ». В

технической литературе ее обычно называют антидизъюнкцией или

функцией Вебба (а также функцией Даггера).

Функция f9 называется эквиваленцией (или эквивалентностью) x1 и x2 , обозначается x1 ~ x2 или x1 ≡ x2 , или x1 ↔ x2 , и читается « x1 эквивалентно x2 ».

Функция	f13	называется импликацией		x1 и x2 ,	обозначается
x1 → x2 или x1 x2 , и часто читается « x1 имплицирует x2						» или «из
x1 следует x2 ».
Функция	f14		называется штрихом	Шеффера	x1	и x2 ,
обозначается x1 \|		x2	и часто читается «не x1 или не x2 » или « x1 и x2

не совместны». В технической литературе ее обычно называют

антиконъюнкцией.

Символы из множества B = {¬, &, , , ~, →, ↓, |} , в алгебре

логики участвующие в обозначениях элементарных функций, называют

логическими связками.

Задачи для самостоятельного решения

1. Найти номера следующих двоичных наборов:

а) (1010); б) (1001001); в) (0011001110); г) (10 K01), k ≥1 ;

123

		k раз
д) (1K10 K0), m, k ≥1	; е) (10 K01K10 K01), k ≥1 .
{ 123	123	{123
m раз k раз	k раз	k раз k раз

2.	Найти двоичный набор длины k , являющийся разложением числа n :
а) k = 6, n = 54 ; б) k =11, n = 2000 ;
в) k = m +1, n = 2m +1 ; (m ≥1) ; г) k = m, n = 3 2m−2 −1 (m ≥ 2) .
3.	Для сравнимых наборов множества A из Bn выписать их в порядке

предшествования ( p ). Выяснить, имеются ли в множестве A соседние

и противоположные наборы, и, если они имеются, выписать их:

а) A = {(001), (010), (101), (100), (110), (111)};

б) A = {(00111), (01011), (00110), (10110), (11010), (01010), (11100), (11011)}.

4. Найти:

~ n

из B

, имеющих вес k ( n ≥ k ≥ 0, n ≥1 );

а) число наборов α

~ n

из B

, удовлетворяющих условию

б) число наборов α

n−1

~ n

) < 2

( n ≥1 );

≤ν(α

в) число упорядоченных пар соседних наборов в B n ( n ≥1 );

~ n

) наборов из B

, таких, что

г) число упорядоченных пар (α

, β

~ n

) = k ( n

≥ k ≥1 );

ρ(α

, β

~ n

из B

веса k , у которых между любыми

д) число наборов α

единичными компонентами находится не менее r нулевых компонент

( n − 2 ≥ r ≥ 0, n ≥ k ≥ 2 ). 5. Показать, что:

а) два различных набора в Bn , имеющих одинаковый нес, несравнимы; б) в Bn существуют только два сравнимых противоположных набора;

в) всякое подмножество наборов в B n , содержащее не менее n + 2 наборов, содержит пару несравнимых наборов ( n ≥ 2 );

г) число наборов в B							n			~ n	,
								, не сравнимых с фиксированным набором α
имеющим вес k , равно 2n − 2n−k − 2k +1 ( n ≥ k ≥ 0, n ≥1 ).
6. Найти число функций в P2 (n) , удовлетворяющих условиям:
а) на данных k				наборах значения функции фиксированы, а на
остальных произвольные ( 2n−1 ≥ k ≥1, n ≥1 );
					~ n			из B	n	, удовлетворяющих условию
б) число наборов α
2	n−1	~ n	) ≤ 2		n	( n ≥1 );
		≤ν(α
в) число упорядоченных пар соседних наборов в B n ( n ≥1 ).
7. Найти число функций в P2 (n) , удовлетворяющих условию:
а) на данных k				наборах значения функции фиксированы, а на

остальных произвольные ( 2n −1 ≥ k ≥1, n ≥1);

б) на противоположных наборах функция принимает одинаковые значения ( n ≥1 );

в) на каждой паре соседних наборов функция принимает противоположные значения ( n ≥1 );

г) функция равна 0 не менее чем на половине наборов ( n ≥1 ).

8. а) На аварийном пульте системы расположены четыре сигнальные лампочки L1 , L2 , L3 , L4 . Система выключается только в том случае, когда выполняется хотя бы одно из следующих условий: а) загорелась лампочка L1 , но не загорелась лампочка L2 ; б) загорелись лампочки

L2 и L3 , но не загорелась лампочка L4 ; в) загорелась лампочка L4 и

		~	булевой
не горит лампочка L1 . Построить вектор значений α f
	~ 4	) , характеризующей условия выключения системы, т.е.
функции f (x
~ 4	) =1 тогда и только тогда, когда справедливо хотя бы одно из
f (x

условий а), б), в); при этом предполагается, что xi =1 , если лампочка Li горит, и xi = 0 , если лампочка Li не горит.

б) Четырем членам B1 , B2 , B3 , B4 некоторой комиссии

сформулированы следующие условия посещения заседаний (хотя бы одно из них они должны выполнить): а) в заседании не участвует ни

B1 , ни B2 , но должен быть B3 ; б) в заседании принимают участие B2 и B4 , но отсутствует B3 ; в) на заседании должны присутствовать B1 и B4 . Обязан ли присутствовать на заседании член B3 ; если в нем не участвует B2 ?

9. Указать все фиктивные переменные у функции f :

~3	) = (10101010)	~ 4	) = (1011010110110101) ;
а) f (x		; б) f (x

~ 4 =

в) f (x ) (0101111101011111) .

10. Через P2c (n) обозначим множество всех булевых функций , зависящих от переменных x1 , x2 , K, xn и притом от каждой из них существенным образом.

а) Выписать все функции множества P2c (2) .

б) Найти число элементов множества Pc (3) .
2
в) Доказать, что число элементов множества	Pc (n) равно
	2
n
∑(−1)k Cnk 22n−k .
k =0
Ответы

1. а) 10; б) 73; в) 206; г) 2k +1 +1; д) 2m+k − 2k ; е)

23k +1 + 22k +1 − 2k +1 +1 . 2. а) (110110); б) (11111010000); в)

n = (10 K01)	; г) при m ≥ 4	n = 2m−1 + 2m−2 −1 и n = (10 1K1 ) ;
123		{
k−1 раз		k −2 раз

при m = 3 n = (101) ; при m = 2 n = (10) . 3. а) (001) p (101) p (111); (010) p (110)}; (101) p (111); соседние: (001) и (101), (010) и (110), (101) и (100), (101) и (111), (110) и (111); противоположные (001) и (110), (010) и (101); б) (00110) p (00111), (00110) p (10110),

(01010) p (01011) p (11011), (01010) p (11010) p (11011); шесть пар соседних наборов; противоположных наборов нет. 4. а) Cnk ; б) 2n−1 ;

в) n 2n−1 ; г) Cnk 2n . Указание. Любой набор, отстоящий от

~ n	~ n
фиксированного набора α	на расстоянии k , получается из α

подходящей заменой некоторых k компонент на противоположные. д)

C k− − . n r(k 1)

6. а) Cnk ; б) 2n−1 ; в) n 2n . 7. а) 22 n −k ; б) 22 n−1 ; в) 2;

		2 n	−1		1		2 n−1		~
г)	2			+		C		n	. 8. а) α f	= (0101011111110010) ; б) Нет.
г)	2			+	2	C	2	n	. 8. а) α f	= (0101011111110010) ; б) Нет.
					2		2

Указание. Предполагая, что xi =1 , если член Bi присутствует на заседании, и xi = 0 , если отсутствует, условия задачи с помощью булевой функции можно представить в виде

<<< < Предыдущая 12 / 222 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

x1	x2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

x1	x2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

x1	x2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1