
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание
§2.4. Раскраски графов. Планарность
Определение. Пусть задано несколько красок k1, k2 , ..., ks . Раскраской
графа G называется правило, по которому каждой вершине графа присваивается номер 1 ≤ i ≤ s , соответствующий краске, причем смежные вершины имеют разные номера.
Определение. Хроматическим числом χ(G) графа G называется
наименьшее число красок, требуемое для раскраски данного графа. Для полного графа χ(Kn ) = n .
Определение. Граф называется бихроматичным, если для его раскраски требуется две краски ( χ(G) = 2 ).
Теорема (Критерий бихроматичности). Для любого графа G эквивалентны условия:
(1)Граф G бихроматичен;
(2)граф G двудольный;
(3)в графе G нет циклов нечетной длины. Доказательство. Будем доказывать эквивалентность по схеме
(1)(3) (2) (1) .
(1) (3) Пусть граф G бихроматичен. Нужно доказать, что в нем нет циклов нечетной длины. Предположим, что цикл нечетной длины существует: v1, v2 , ..., v2k −1 . В силу бихроматичности, нечетные вершины одного цвета. Следовательно, вершины v1 и v2k −1 одного
цвета, но они смежные. Получили противоречие. Циклов нечетной длины нет.
(3) (2) Пусть в графе G нет циклов нечетной длины. Нужно доказать, что G двудольный. Пусть – компоненты
связности графа G. Достаточно доказать, что каждая компонента связности является двудольным графом. Поэтому можно считать G связным графом, т.е. любые две вершины в нем соединены путем. Введем на множестве вершин графа V отношение “~” следующим образом: a ~ b , если существует путь четной длины из вершины a в вершину b . Если из a в b существует путь четной длины, то из a в b не существует пути нечетной длины, иначе нашелся бы цикл нечетной длины.
Докажем, что “~” – отношение эквивалентности. Действительно, оно рефлексивно: a ~ a (из a в a существует путь длины 0); симметрично:
если a ~ b , то b ~ a (если из a в b существует путь четной длины, то существует путь четной длины из b в a ); транзитивно: если a ~ b и b ~ c , то a ~ c (если существует пути четной длины из a в b и из b в c , то существует пути четной длины из a в c . Следовательно, множество вершин графа V разбивается на два класса эквивалентности V1 и V2 : V1 – множество вершин графа, до которых из фиксированной вершины а существует путь четной длины, V2 – множество вершин графа, до которых из фиксированной вершины а существует путь нечетной длины. Тогда концы произвольного ребра лежат в разных множествах V1 и V2, иначе для двух вершин одного множества существовал бы путь длины 1 по этому ребру. Следовательно, граф G двудольный.
(2) (1) Пусть G – двудольный граф. Нужно доказать, что он
бихроматичен. Так как смежные вершины графа принадлежат разным долям, то вершины одной доли раскрасим в один цвет, второй – в другой. Теорема доказана.
Определение. Реберным хроматическим числом χp (G) графа G
называется наименьшее количество красок, необходимых для раскраски ребер графа таким образом, чтобы смежные ребра имели разные цвета.
n, если п нечетно, Для полных графов χp (Kn ) = n −1, если п четно.
Если ∆(G) = max deg v, то, очевидно, ∆(G) ≤ χp (G) .
v VG
Справедлива теорема Визинга. ∆(G) ≤ χp (G) ≤ ∆(G) +1.
Планарные графы
Определение. Граф G называется планарным, если его можно изобразить на плоскости без пересечения ребер.
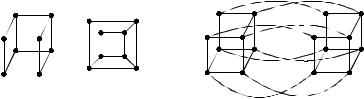
Пример. Трехмерный куб В3 является планарным (рис. 2.49), четырехмерный куб В4 – нет (рис. 2.50). Полный граф К4 является планарным (рис. 2.51), полный граф К5 – нет (рис. 2.52).
Рис. 2.49 |
Рис. 2.50 |

|
|
Пусть G – планарный |
|
|
связный граф. Тогда |
|
|
любой простой цикл в |
|
|
нем определяет |
|
|
|
|
|
некоторую область на |
Рис. 2.51 |
Рис. 2.52 |
R2. Эта область |
|
|
называется гранью. У |
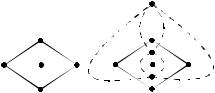
графа есть ровно одна неограниченная грань – она называется океаном
(рис. 2.53).
Теорема (Эйлера). В любом планарном связном |
океан |
|
|||
графе В+ Г = Р+ 2 , где В– количество вершин, |
|
||||
Г – граней, Р |
– ребер. |
|
грань |
|
|
Доказательство. проведем индукцией по числу |
|
|
|
||
ребер. При Р =1 В = 2 , Г =1(океан), и равенство |
Рис.2.53 |
||||
В+ Г = Р+ 2 |
выполняется. |
||||
|
|
|
|||
|
Предположим, что |
||||
e |
утверждение верно при |
||||
любом числе ребер, |
|||||
меньшем п, и докажем
eравенство для графа с п ребрами. Пусть G –
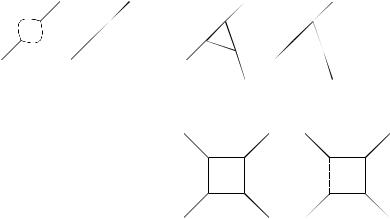
Рис. 2.54 произвольный граф, Р = n . Возьмем произвольно ребро е графа G, и удалим его, если оно висячее, то вместе с соответствующей вершиной. Если ребро было висячим, то для нового графа G' имеем В'= В−1, Г'= Г , Р'= Р−1 (рис. 2.54а). Так как число ребер у G' меньше, чем у G, то по индукционному предположению В'+Г' = Р'+2 и, следовательно, В+ Г = Р+ 2 . Если было удалено невисячее ребро (рис. 2.54б), то В'= В, Г'= Г −1,
Р'= Р−1. Аналогично, В'+Г' = Р'+2 и, следовательно, В+ Г = Р+ 2 . Теорема доказана.
Пусть G – планарный граф. Если у него есть висячие ребра, то добавим произвольные ребра, чтобы висячих не осталось. При этом хроматическое число χ(G) может только увеличится. Граф без висячих
вершин будем называть замкнутым. Далее рассматриваются планарные графы без петель, но в которых могут быть кратные ребра.
Определение. Пусть G – планарный граф. Построим граф G* следующим образом. Число вершин графа G* равно числу граней G . Каждой грани G поставим в соответствие вершину G*. Вершины в G*
смежны тогда и только тогда, когда соответствующие им грани в G граничат по ребру, причем две вершины G* соединяет столько ребер, сколько общих граничных ребер у соответствующих им граней. Граф
G* называется двойственным (сопряженным) графу G.
В |
качестве |
примера |
|
|
|
|
||
построим |
|
|
граф, |
|
|
|
|
|
сопряженный |
графу |
G , |
|
|
|
|
||
изображенному |
на |
рис. |
|
|
|
|
||
2.55а. Каждой грани G |
|
|
|
|
||||
|
|
|
|
|||||
соответствует единственная |
|
|
|
|
||||
|
|
|
|
|||||
вершина G*. Изобразим ее |
|
|
|
|
||||
внутри |
грани. |
|
Если |
а) |
|
б) |
||
вершины а* |
и b* графа G* |
|
Рис. 2.55 |
|||||
лежат |
в соседних гранях, |
|
||||||
|
|
|
|
|||||
граничащих по ребрам e1, e2 , ..., es , соединим ребрами e1*, e2*, ..., es *, пересекающими e1, e2 , ..., es . Ребра ei графа G и ei * графа G* , i =1, 2, ..., s , называются перпендикулярными (рис. 2.55б).
При этом внутри каждой грани графа G* лежит единственная вершина графа G. Действительно, предположим, что внутри некоторой грани γ*
графа G* находятся несколько вершин a1, a2 , ..., as графа G. Так как из
каждой вершины выходит по крайней мере одно ребро, а каждое ребро γ* пересекает ровно одно ребро графа G, то s ≤ n , где п – число
ребер грани γ* . Тогда, если какие-либо две из вершин соединены ребром, то внутри грани γ* найдется ребро e* , пересекающее это
ребро, чего быть не может, так как внутри грани ребер нет. Пусть никакие две из вершин графа G, находящиеся внутри γ* , не соединены
ребром. Тогда все ребра, выходящие из этих вершин, пересекают ребра грани γ* . Так как каждое ребро графа G * пересекает ровно одно
s
ребро графа G, то ∑deg(as ) = n , где п – количество ребер и,
i=1
соответственно, вершин грани γ* . Проведение первого ребра из
каждой вершины не меняет число компонент связности плоской области, ограниченной гранью, проведение каждого следующего, начиная со второго увеличивает число компонент связности на 1. Таким
образом, в результате проведения всех ребер из вершин a1, a2 , ..., as ,
число компонент связности области, ограниченной гранью, не превышает n −1 . Так как количество вершин грани γ* равно п, то
найдутся две вершины, лежащие в одной компоненте связности. Но тогда они принадлежат одной грани графа G, что противоречит определению сопряженного графа.
Таким образом, существует взаимно-однозначное соответствие между гранями G и вершинами G*, вершинами G и гранями G*, ребрами G и G*.
Теорема Эйлера (о пяти красках). Хроматическое число планарного графа не превосходит 5.
Доказательство. Достаточно рассмотреть только замкнутые графы, так как из всякого незамкнутого графа можно получить замкнутый добавлением ребра, что не уменьшает хроматического числа. Пусть G – планарный граф, G* – сопряженный ему. Тогда
В* = Г, Г* = В, Р* = Р. Тогда вместо вершин можно раскрашивать
грани.
Докажем теорему сначала для графов, степени всех вершин которых равны 3. Предварительно докажем лемму.
Лемма. Пусть G – граф, у которого d(vi ) = 0 для любой вершины vi . Тогда в нем существует грань, в которой не больше 5 ребер. Пусть
nk – количество k-угольных граней в G , ∑nk = Г . Тогда k nk –
k
количество ребер в k-угольных гранях. В сумме ∑k nk каждое ребро
считается ровно два раза, поэтому ∑k nk |
k |
= 2Р = ∑deg(vi ) . Так как |
|
k |
i |
степени всех вершин равны 3, имеем ∑k nk = 3V . Воспользовавшись
k
формулой В+ Г = Р+ 2 , получим
13 (2n2 + 3n3 +...)+ (n2 + n3 +...)= 12 (2n2 + 3n3 +...)+ 2 , n2 + n3 +... = 16 (2n2 +3n3 +...)+ 2 ,
6(n2 + n3 +...)= 2n2 +3n3 +... +12 ,
4n2 +3n3 + 2n4 +1n5 + 0n6 − n7 − 2n8 −... =12 ,
4n2 +3n3 + 2n4 +1n5 = n7 + 2n8 +12 .
Если в графе нет двух-, трех-, четырех-, пятиугольников, то n2 = n3 = n4 = n5 = 0 и 0 = n7 + 2n8 +12 > 0 . Получили
противоречие, следовательно, в графе есть хотя бы один из двух-, трех-, четырех-, пятиугольников. Лемма доказана.
Доказательство теоремы для случая, когда степени всех вершин равны 3, проведем индукцией по числу граней графа. Предположим, что для всех графов с числом граней, меньшим п, утверждение верно и докажем для графа с п гранями. По лемме, в графе есть хотя бы один из двух-, трех-, четырех-, пятиугольников.
1) Есть двухугольник (рис. 2.56а). Объединим его с одной из соседних граней. Для нового графа (рис. 2.56б) по индукционному предположению существует раскраска пятью красками. Возвращаясь к исходному графу, раскрашиваем двухугольник в цвет, отличный от цвета двух соседних с ним граней.
2) Есть треугольник (рис. 2.57а). Объединим его с одной из соседних граней. Для нового графа (рис. 2.57б) по индукционному предположению существует раскраска пятью красками. Возвращаясь к исходному графу, раскрашиваем треугольник в цвет, отличный от цвета трех соседних с ним граней.
а) |
б) |
а) |
б) |
|
Рис. 2.56 |
|
Рис. 2.57 |
3) Есть четырехугольник (рис.
2.58а). Объединим его с одной из соседних граней. Для нового
графа (рис. 2.58б) по индукционному предположению существует раскраска пятью
а) б)
Рис. 2.58
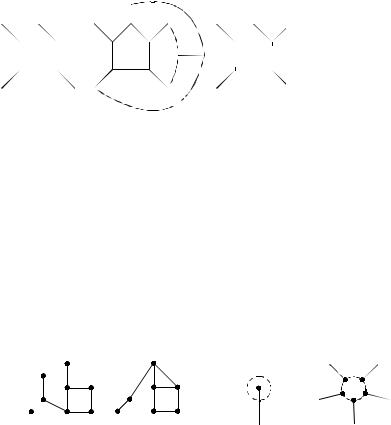
красками. Возвращаясь к исходному графу, раскрашиваем четырехугольник в цвет, отличный от цвета четырех соседних с ним граней.
4) Есть пятиугольник (рис. 2.59а). Тогда из граничащих с ним граней найдутся две противоположные, которые не граничат между собой. Действительно, пусть L1 и L3 – противоположные грани, граничащие
|
|
|
|
|
|
|
|
|
|
между собой (рис. |
|
L5 |
|
L1 |
k5 |
|
|
k1 |
2.59б). Тогда L2 не |
||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
граничит ни с L4, ни |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
L2 |
|
|
|
|
k2 |
|
с L5. |
L4 |
|
|
|
|
|
|
|
Объединим |
||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
пятиугольник с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k3 |
||
|
|
L3 |
|
|
|
|
гранями L2 и L4. Для |
|||
|
|
|
|
|
|
|
|
нового графа (рис. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.52в) по |
а) |
|
|
б) |
|
|
в) |
индукционному |
|||
|
|
|
|
|
|
|
|
|
|
предположению |
Рис. 2.59 |
существует |
|
раскраска пятью красками. Возвращаясь к исходному графу, раскрашиваем L2 и L4 тем цветом, который был у объединенной грани, пятиугольник в оставшийся пятый цвет. Теорема доказана для графа, у которого степени всех вершин равны 3 .
Пусть теперь G – граф с произвольными степенями вершин. Если степень вершины равна 2, то мы можем просто ее удалить, вместо двух ребер составив одно. Это не повлияет на существование границ между гранями (рис. 2.60). Если степень вершины равна п ≥ 4, заменяем ее на п-угольник (рис. 2.61). Степени образовавшихся новых вершин равны 3. Для нового графа существует раскраска пятью красками. Возвращаясь к исходному графу, получаем ту же раскраску и для него.
Рис. 2.60 |
Рис. 2.61 |
Теорема полностью доказана.
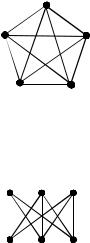
Рассмотрим теперь проблему планарности графов. Теорема. Полный граф K5 не планарный.
Доказательство. Для графа K5 (рис. 2.62) имеем В = 5, Р =10 . Если бы он был планарный, то вы-
полнялось бы равенство В+ Г = Р+ 2 , т.е. Г = 7 . Двухугольные грани, очевидно, отсутствуют.
Имеем n2 = 0, n3 + n4 +... = 7 . Кроме того, 3n3 + 4n4 +... = 2Р = 20 . Умножим первое равенство на 3 и отнимем из второго. Получим n4 + 2n5 +... = −1. Получили противоречие, следовательно, граф K5 не планарный.
Теорема. Полный двудольный граф K3,3 не планарный.
Доказательство. Для графа K3,3 (рис. 2.63) имеем В = 6, Р = 9 . Если бы он был планарный, то
выполнялось бы равенство В+ Г = Р+ 2 , т.е.
Г = 5 .
Имеем n2 = 0, n3 + n4 +... = 5 . В силу того, что
Рис.2.62
Рис. 2.63
общее количество ребер 9, в графе не может быть граней с большим,
чем |
9, |
числом |
ребер. |
Получаем |
n3 + n4 +... + n9 = 5 , 3n3 + 4n4 +... + 9n9 = 2Р =18 . |
Так как граф K3,3 |
|||
двудольный, то по критерию бихроматичности в нем нет циклов нечетной длины, следовательно, нет граней с нечетным числом ребер:
n3 = n5 = n7 = n9 = 0 . Имеем
n4 + n6 + n8 = 5 , 4n4 + 6n6 +8n8 =18 . Умножив первое равенство на 4 и вычтя его из второго, получим 2n6 + 4n8 = −2 . Противоречие, граф
K3,3 не планарный.
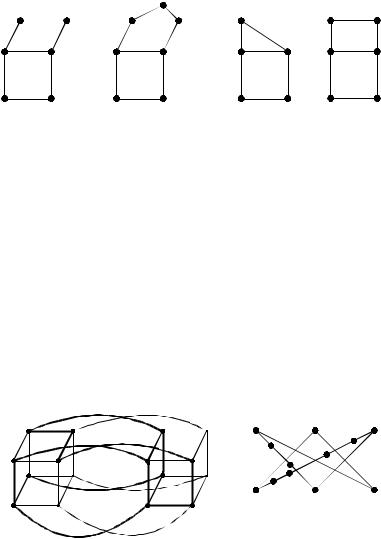
Определение. Пусть задан граф G, е =(а, b) – произвольное ребро. Операцией разделения ребра будем называть добавление к множеству V(G) одной вершины c и замену одного ребра е на два e'= (a, c) и
e"= (c, b) (рис. 2.64).
а е b |
а |
e/ c e// |
||
|
|
|
|
b |
Рис. 2.64 |
Рис.2.65 |
Определение. Графы G1 и G2 называются гомеоморфными, если существуют изоморфные графы G1' и G2', полученные из графов G1 и G2 применением один или несколько раз операции разбиения ребер.
Пример. Графы на рис. 2.65 не изоморфны, но гомеоморфны. Если граф содержит непланарный подграф, то он сам не планарен.
Теорема (Критерий планарности А.С. Понтрягина – К.
Куратовского). Граф G планарный тогда и только тогда, когда у него нет подграфов, гомеоморфных K5 или K3,3.
Пример. Доказать, что четырехмерный куб В4 не планарен.
Рассмотрим подграф графа В4, образованный вершинами K1, K2, K3, D1,
D2, D3, Х1, Х2, Х3, Х4, Х5, Х6 и ребрами (D1, K1), (D1, K2), (D1, K3), (D1, K1), (D2, K1), (D2, K3), (D2, X1), (X1, X2), (X2, K2), (D3, K2), (D3, K3), (D3, X3), (X3, X4), (X3, X4), (X4, X5), (X5, K1) (рис.2.66а).
Этот подграф гомеоморфен K3,3 (рис. 2.66б). Следовательно, граф В4 не планарен.
|
K1 |
|
X6 |
D2 |
X5 |
|
|
|
X2 |
K2 |
|
D1 |
X4 |
|
|
K3 |
X1 |
D3 |
X3 |
D1 |
|
D |
D |
|||||
|
2 |
X3 3 |
||||||
|
|
|
|
|
|
X4X3 |
|
|
|
|
|
|
|
|
|
||
|
|
X1 |
X2 |
|
|
X2 X4 |
|
|
|
|
X6 |
X5 |
|
|
|
|
|
|
2 |
K3 |
||||||
K1 |
|
K |
|
|
||||
а) |
б) |
Рис. 2.66
Задачи для самостоятельного решения
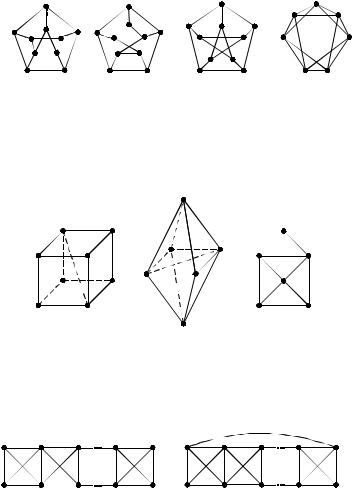
1.Является ли планарным граф K5 , из которого удалено одно ребро?
2.Являются ли планарными графы, изображенные на рис.2.67?
а) |
б) |
в) |
г) |
Рис. 2.67
3.Является ли планарным граф, получающийся из B3 добавлением главной диагонали (рис. 2.68а)?
4.В октаэдре соединены две противоположные вершины (рис. 2.68б). Является ли получившийся граф планарным?
а) |
б) |
в) |
Рис.2.68
5.Планарен ли граф C3 ×Z5 ?
6.При каких значениях п ≥ 2 планарен граф (см. рис. 2.69)?
а) |
б) |
Рис. 2.69
