Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Дискретная математика

Файл:

Литература / Учебник (Кожухов, Прокофьев, Соколова) / discret_mat.pdf

Скачиваний:

562

Добавлен:

16.04.2013

Размер:

2.43 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 226 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

§1.6. Дизъюнктивная нормальная форма

~3 =

Пример. Рассмотрим функцию f (x ) (01001100) . Приведем несколько различных формул, являющихся д. н. ф. и реализующих функцию f . Это ее СДНФ = x1 x2 x3 x1 x2 x3 x1 x2 x3 и д. н. ф.: f1 = x1 x2 x2 x3 , f2 = x1 x2 x3 x2 x3 , f3 = x1 x2 x1 x2 x3 .

Заметим, что f = f1 = f2 = f3 .

Лемма. Число различных д. н. ф. от переменных x1 , K, xn равно 23n . Доказательство. Действительно, число различных элементарных

конъюнкций K = xiσ1 Kxiσr равно 3n (“пустой” конъюнкции
1	r

сопоставлена константа 1), так как для каждой переменной xi имеется

три возможности: присутствует в конъюнкции, присутствует с отрицанием и отсутствует. Выпишем все элементарные конъюнкции,

поставив между ними дизъюнкции: D = K1 K K n . Удаляя

1442443

различные Ki , получим все возможные д. н. ф. Следовательно, число

различных д. н. ф. равно 23n и одной функции соответствует несколько различных д. н. ф.

Введем функционал L(D) , означающий сложность д. н. ф., обладающий свойствами:

1.L(D) ≥ 0 .

2.Если D = D′ xiσi K ′, то L(D) ≥ L(D′ K ′) .

3.Если D = D1 D2 и D1 D2 ≡ 0 , то L(D) ≥ L(D1 ) + L(D2 ) .

4.Если D и D′ получены одна из другой переименованием переменных, то L(D) = L(D′) .

Примеры: 1) LБ (D) – число букв в д. н. ф.; 2) LK (D) – число элементарных конъюнкций; 3) LO (D) – число знаков отрицаний. Тогда для рассмотренного в начале параграфа примера:

LБ ( f ) = 9 , LБ ( f1 ) = 4 , LБ ( f2 ) = LБ ( f3 ) = 5 ; LK ( f ) = 3 , LK ( f1 ) = LK ( f2 ) = LK ( f3 ) = 2 ; LO ( f ) = 5 , LO ( f1 ) = 2 , LO ( f2 ) = LO ( f3 ) = 3 .

Определение. Д. н. ф. D называется минимальной для данной функции f , если L(D) имеет минимальное значение.

Проблема минимизации д. н. ф. состоит в том, каким образом для произвольной функции f построить минимальную д. н. ф. Конечно,

существует алгоритм, реализующий проблему минимизации, – это алгоритм полного перебора. Однако этот алгоритм занимает слишком много времени и для функций, зависящих от большого числа переменных, реализован быть не может. В связи с этим важное значение приобретают методы, позволяющие за реальное время получить д. н. ф., в той или иной степени приближенные к минимальной.

Процедура упрощения д. н. ф.

1. Удаление элементарной конъюнкции, которая представима в виде

D = D′ K . D f – реализует функцию f и если D′f	– тоже
реализует функцию f , тогда мы можем отбросить K	′
реализует функцию f , тогда мы можем отбросить K	. L(D) ≥ L(D ) .

2. Удаление множителя. Для двух д. н. ф. D = D′ xiσ K ′ и D′ K ′ таких, что (D′ K ′) f = D f , L(D) ≥ L(D′ K ′) .

Определение. Д. н. ф., которую нельзя упростить с помощью вышеприведенных методов, называется тупиковой.

) = (01001100) д. н. ф. x1 x2 x3 x2 x3

Примеры: Для функции f (x

– не тупиковая, а x1

2 x3

– тупиковая.

Алгоритм получения тупиковой д. н. ф.

1. По функции f строят какую-либо д. н. ф. (с уверенностью можно

говорить о построении хотя бы СДНФ). В д. н. ф. фиксируют порядок слагаемых и в каждом слагаемом порядок множителей.

2. Просматривают слева направо д. н. ф. каждую элементарную конъюнкцию на предмет упрощения:

а) возможность удаления элементарных конъюнкций; б) возможность удаления множителя.

3. Возврат в п.2а, проводя то же (не просматривая множители).

~3 =

Например, для функции f ( x ) (01001100) .

f = x1 x2 x3 x1 x2 x3 x1 x2 x3 = x2 x3 x1 x2 x3 x1 x2 x3 =

= x2 x3 x1 x2 (x3 x3 ) = x2 x3 x1 x2 . Получили тупиковую д. н. ф. при данном порядке следования конъюнкций и букв.

~ n	) P2 (n) и	D – ее
Теорема (без доказательства). Пусть f (x

тупиковая д. н. ф. Тогда существует такое упорядочение СДНФ, что при помощи данного алгоритма получается D .

Рассмотрим также геометрическую интерпретацию построения д. н. ф. на единичном кубе.

Геометрическая интерпретация

Каждой булевой функции				~ n	)	в булевом кубе B	n	можно поставить
				f (x
в соответствие множество его вершин, называемое носителем f ,
		N f ={(α1 , K, αn )\| f (α1 , K, αn ) =1} .
Очевидно, множество N f				однозначно определяет функцию f .
Если функция реализуется элементарной конъюнкцией
K(x , K, x	n	) = xα1 Kxαr , то соответствующее множество N							K
1		i1	ir

называется интервалом r -го ранга ( N K есть (n − r) -мерная грань

Bn ). Очевидно, что если

f (x1 , K, xn ) =ϕ(x1 , K, xn ) ψ (x1 , K, xn ) , то N f = Nϕ Nψ .

Для функции f , реализуемой д. н. ф. K1 K Km , справедливо равенство N K = N K1 K N Km . Если ri − ранг Ki , то число

m
r = ∑ri называется рангом покрытия.
i=1
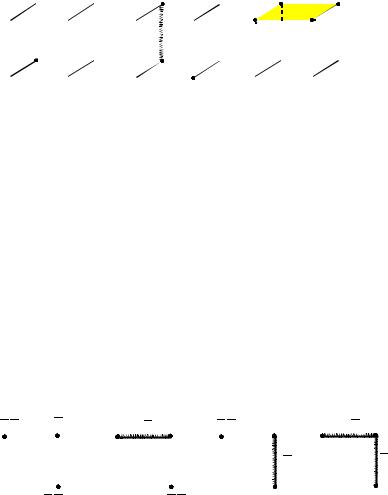
Примеры. Носитель N f функции
~3	) = (01001100) показан на рис. 1.2.
f (x

1,1,0		1,1,1
0,1,0		0,1,1
0,1,0

	1,0,0		1,0,1

0,0,0 0,0,1

Рис. 1.2

Для конъюнкции x1

носитель – точка (x1 =1, x2 = 0, x3 = 0)

( n = 3, r = 3 определяют нулевую грань) (см. рис. 1.3а).

Для конъюнкции x1 x3 ранг равен 2, поэтому носитель – ребро

(x1 =1, x3 = 0) (см. рис. 1.3б). Для конъюнкции x2

ранг равен 1;

1,1,0

1,1,1

1,1,0

1,1,1

0,1,0

1,1,0

1,1,1

0,1,0

0,1,1

0,1,0

0,1,1

1,0,0

1,0,1

0,0,0

0,0,1

0,0,0

0,0,1

0,0,0

0,0,1

x2x3

а)

б)

в)

Рис. 1.3

носитель – плоскость ( x2 =1 )(см. рис. 1.3в).

Свойства носителя.

1. Если

f (x1 ,K, xn ) = g(x1 ,K, xn ) h(x1 ,K, xn ) , то:

а) N g N f , Nh N f ;

б) N f = Ng Nh .

3. Для функции, представленной д. н. ф. f = Ki ,

N f = UN Ki .

i=1

Замечание. Проблема построения д. н. ф. сводится к покрытию

носителя f гранями.

)

= (01001100) покрывается

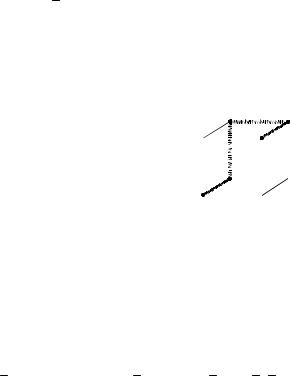
Пример. Носитель функции f (x

а) x1

3 x1

2 x3

1 x2 x3 (рис. 1.4а); б) x1

2 x3

(рис.

2 x3

x3 (рис. 1.4г).

1.4б); в)

(рис. 1.4в); г)

x1x2x3	x1x2x3	x1x2	x1x2x3	x1x2
			x2x3	x2x3

x1x2x3 x1x2x3

а)

б)

в)

г)

Рис. 1.4

Сокращенная д. н. ф.

Определение. Конъюнкция K(x , K, x	n	) = xσ1 Kxσr называется
1		i1	ir
импликантой для функции f , если N K		N f .
Определение. Импликанта называется простой, если из
соответствующей конъюнкции K = xiσ1 Kxiσr			нельзя вычеркнуть ни
1		r

одной переменной, чтобы оставшееся выражение было импликантой.

~3
~3	) = (01001100) конъюнкция	K = x1 x2 x3
Пример. Для функции f (x	) = (01001100) конъюнкция	K = x1 x2 x3
(это импликанта, так как носителем является точка) не является

простой, так как K ′ = x1 x2 – простая импликанта. В геометрической интерпретации импликанта – наибольшая грань.

Определение. Сокращенная д. н. ф. – это дизъюнкция всех простых импликант (она единственна).

Пример. Для функции

) = (01001100) это два ребра

f (x

2 x3 .

1,1,0

0,1,0

1,1,1

Для функции f (x

) =

(10011011)

(рис.

0,1,1

1.5) сокращенная д. н. ф. имеет вид

1,0,0

x2 x3 x1 x3 x1 x2 x2 x3 .

1,0,1

Теорема. Минимальная д. н. ф.

0,0,0

0,0,1

получается из сокращенной

Рис. 1.5

вычеркиванием из нее некоторых простых

импликант.

Аналитические методы построения сокращенной д. н. ф. Метод Нельсона


1.	~ n	) строят СКНФ. Например, для					~3		) = (10011011)
1.	По f (x	) строят СКНФ. Например, для					f (x		) = (10011011)
	СКНФ = (x1 x2			3 )(x1		2 x3 )(			1 x2		3 ) .
	СКНФ = (x1 x2		x	3 )(x1	x	2 x3 )(		x	1 x2	x	3 ) .
2.	Раскрывют скобки.

(x1 x1 x1 x2 x1 x3 x2 x1 x2 x2 x2 x3 x3 x1 x3 x1

x3 x3 ) (x1 x2 x3 ) = (x1 x2 x3 x3 x2 ) (x1 x2 x3 ) = = x1 x1 x1 x2 x1 x3 x2 x3 x1 x2 x3 x2 x2 x3 x3

x3 x2 x1 x3 x2 x2 x3 x2 x3 = x1 x2 x1 x3 x2 x3 x2 x3 . 3. Производим упрощение по следующим правилам:

K K = K ,			K K = K ,
K		= 0 ,	K 0 = K , K1K2 K1 = K1 .
	K
			Метод Квайна

1. По f (x1 , K, xn ) строим СДНФ. Например, для функции

f (x1 , x2 , x3 ) = (01001100) . СДНФ= x1 x2 x3 x1 x2 x3 x1 x2 x3 . 2. Применяем операцию неполного склеивания

xK xK = K xK xK .

3. После того как такая операция применена к каждой паре конъюнкций из СДНФ, к которой она применима, с помощью операции поглощения

( K xσ K = K ) удаляются те конъюнкции ранга n , которые можно удалить таким образом. В итоге получаем некоторую д. н. ф. D1 . 4. Если проведено k ≥1 этапов, то на (k +1) -м этапе операции

неполного склеивания и поглощения применяются к конъюнкции ранга n − k д. н. ф. Dk . Получаем д. н. ф. Dk +1 .

Алгоритм завершается, если Dk+1 = Dk .

Пример. Построить сокращенную д. н. ф. функции f (x1 , x2 , x3 ) = (11001101) .

Решение. D0 = x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .

После первого этапа имеем D1 = x1 x2 x1 x2 x1 x2 x3 . После второго этапа имеем D2 = x1 x1 x2 x3 .

Определение. Простая импликанта K называется ядровой, если

существует набор (α1 , K, αn ) Bn такой, что K(α1 , K, αn ) =1, но K ′(α1 , K, αn ) = 0 для всех K ′, входящих в сокращенную д. н. ф.

Геометрическая интерпретация: K – ядровая импликанта, если

существует точка, принадлежащая N f								Bn , которая покрывается
только N K .				~3
				~3			) = (10011011) сокращенная д. н. ф. =
Пример. Для функции f (x							) = (10011011) сокращенная д. н. ф. =
				x1		3 x1 x2		x2 x3
=		x	x	x1	x	3 x1 x2		x2 x3	.
	123							{
	ядровая импликант						ядровая импликанта

Определение. Ядровая д. н. ф. (ЯДНФ) – это дизъюнкция всех ядровых импликант.

Пример. На рис. 1.6 представлен носитель функции, у которой нет ядровой д. н. ф.

1,1,0	1,1,1
0,1,0	0,1,1
	0,1,1
1,0,0
	1,0,1
0,0,0	0,0,1
Рис. 1.6

Задачи для самостоятельного решения

1. Из заданного множества A элементарных конъюнкция выделить простые импликанты функции f :

а)

A ={x1 , x3 , x1 x2 , x2 x3},

) = (00101111) ;

f (x

б)

A ={x1 x2 , x2 x3 , x1 x2 x3},

) = (01111110) ;

f (x

в)

~ 4

) = (1010111001011110) .

A ={x1 , x4 , x2 x3 , x1 x2 x4 }, f (x

Построить сокращенную д. н. ф. по заданной к. н. ф.:

а) (x1 x2 x3 )(x1 x2 x3 )(x2 x3 ) ;

б) (x1 x2 x3 )(x1 x2 x4 )(x2 x3 x4 )(x1 x4 ) .

3. Используя алгоритм Квайна построить сокращенную д. н. ф. функции f :

а)

) = (11001110) ; б)

) = (1100111110011101) .

f (x

Изобразив множество N f

функции f в B n , найти ее простые

импликаты, построить сокращенную и ядровую д. н. ф.:

а)

) = (11110100) ;

f (x

б)

~ 4

) = (1111100001001100) .

f (x

Найти длину сокращенной д. н. ф. функции f

~ n

) = x1 x2 K xn ;

а) f (x

~ n

) = (x1 x2 x3 )(x1 x2 x3 ) x4

xn .

б) f (x

Показать, что число функций, для которых фиксированная

элементарная конъюнкция ранга r является импликантой, равно

22n − 2n−r .

Показать, что любая функция от n переменных может быть

реализована д. н. ф., содержащей не более 2n−1 элементарных

конъюнкций.

Показать, что число конъюнкций в тупиковых д. н. ф. не превосходит

2n .

~ n

Показать, что число ядровых импликант функции

)

не

f (x

превосходит 2n−1 .

~ n

10. Показать, что вякая простая импликанта функции

) :

f (x

а) ранга n является ядровой;

б) ранга меньше 2 является ядровой.

Ответы

1. а) x1 , x2 x3 ; б) x1 x2 ; в) x2 x3 , x1 x2 x4 . 2. а) x1 x3 x1 x2 x3 ; б) x1 x2 x1 x2 x4 x1 x3 x4 . 3. а) x2 x1 x3 ; б) x1 x2 x1 x3

x2 x4 x3 x4 x1 x2 x4 . 4. а) сокращенная, она же ядровая д. н. ф. x1 x2 x3 ; б)

<<< < Предыдущая 1 2 3 4 56 / 226 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>