
- •Предисловие
- •§1.2. Функции алгебры логики
- •§1.3. Формулы. Реализация булевых функций формулами
- •§1.4. Специальные представления булевых функций
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •§1.6. Дизъюнктивная нормальная форма
- •§1.7. Схемы из функциональных элементов
- •Глава 2. Графы
- •§2.1. Основные определения
- •§2.2. Способы задания графов
- •§2.3. Связность
- •§2.4. Раскраски графов. Планарность
- •§2.5. Потоки в сетях
- •Глава 3. Автоматы
- •§3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •§3.4. Приведённый автомат
- •§3.6. Теоремы Мура
- •§3.7. Ограниченно-детерминированные функции. Информационное дерево
- •§3.8. Синтез автоматов
- •§3.9. Алгебраический подход к теории автоматов
- •Глава 4. Алгоритмы и машины Тьюринга
- •§4.1. О понятии алгоритма. Тезис Чёрча
- •§4.2. Машина Тьюринга
- •§4.3. Рекурсивные функции
- •§4.4. Алгоритмически неразрешимые задачи
- •Содержание

Глава 3. Автоматы
§3.1. Определение и примеры автоматов
Функционирование автоматического устройства, работающего в дискретном режиме времени по заданному закону (определённому, например, схемой этого устройства), может быть описано на математическом языке с помощью понятия конечного автомата. В математической теории предполагается, что автомат V имеет конечное
множество состояний Q ={q1 , ... , qn }, входной алфавит
A ={a1 , ... , am }, выходной алфавит B ={b1 , ... , bk }, причём в дискретные моменты времени t = 0,1,2,... он принимает входной символ a A, изменяет (или сохраняет) своё состояние и выдаёт на выходе символ b B. Изменение (или сохранение) состояния и символ b B на выходе автомата зависят от предыдущего состояния и
a(1)a(2)a(3)... V b(1)b(2)b(3)...
Рис. 3.1
принятого на входе символа a A.
Обозначая через a(i) и b(i) входной и выходной символы, соответствующие моменту времени t = i, мы получим, что автомат V перерабатывает входную последовательность a(1)a(2)a(3)... в выходную последовательность b(1)b(2)b(3)...
Для построения математической теории конечных автоматов необходимо дать строгое определение этому понятию, его мы сейчас приведём.
Определение. Конечным автоматом называется пятёрка V = ( A,Q, B,ϕ,ψ), где A,Q, B − конечные множества, а
ϕ : Q × A → Q и ψ : Q × A → B − отображения.
Отображение ϕ называется функцией переходов, а отображение ψ − функцией выходов. При этом равенство ϕ(q,a) = q' означает, что если автомат V находится в данный момент времени в состоянии q и на его вход пришёл символ а, то к следующему моменту времени он перейдёт в состояние q'. Далее, равенство означает, что если текущее состояние автомата есть q, а на вход поступил символ а,
то на выход будет послан символ b.
Работа автомата описывается системой канонических уравнений:
q(t +1) =ϕ(q(t),a(t)),b(t)=ψ(q(t),a(t)),
которая должна быть дополнена начальным условием q(0) = q0 . Здесь q(0) = q0 Q − начальное, или инициальное состояние.
Замечания.
1.Автомат V = ( A,Q, B,ϕ,ψ), в котором выделено начальное состояние q0 Q, иногда называют инициальным автоматом.
2.Иногда у автомата V выделяют одно или несколько состояний
(скажем, q Q ), называемых конечными, или финальными состояниями. Смысл их состоит в том, что если автомат “попадёт” в состояние q , то он прекращает свою работу.
3.Можно рассматривать вероятностные, или стохастические
автоматы, т.е. такие, в которых переход из одного состояния в другое и формирование выходного символа осуществляются не по жёстко заданному правилу, а с некоторой вероятностью, закон распределения которой должен быть указан. В отличие от вероятностных автоматов обычные автоматы называют
детерминированными.
4.Многие утверждения, касающиеся автоматов, справедливы и без предположения о том, что A, B,Q − конечные множества. Назовём
абстрактным автоматом пятёрку V = ( A,Q, B,ϕ,ψ), где функции ϕ и ψ определяются так же, как и раньше, т.е.

ϕ : Q × A → Q, ψ : Q × A → B, но множества A, B,Q могут быть
бесконечными.
В теории автоматов рассматриваются вопросы исследования поведения автоматов, т.е. реакции автомата на то или иное внешнее воздействие (под которым здесь понимается слово или буква входного алфавита), вопросы синтеза автоматов (т.е. построения автоматов с теми или иными свойствами), а также некоторые другие вопросы. Рассмотрим некоторые примеры автоматов.
Пример 1. Автомат без памяти. Таким автоматом называется автомат, в котором множество  состояний состоит в точности из
состояний состоит в точности из
одного элемента. В этом случае функцию ϕ можно не
рассматривать, а функция ψ
зависит фактически только от пришедшей на вход автомата буквы входного алфавита. Канонические уравнения автомата выглядят здесь
совсем просто:
Так, в частности, работает автомат, который осуществляет перекодировку символов одного алфавита в другой (если при этом одна буква заменяется на другую).
Пример 2. Элемент задержки. У этого автомата входной и выходной алфавиты совпадают: А= е, а выходной символ представляет собой задержанный на 1 такт (на 1 момент времени) входной символ. Таким
a(i) |
|
b(i)=a(i 1) |
образом, b(t +1) = a(t) при всех |
|
Z |
t ≥ 0. Построим этот автомат. Пусть |
|||
|
|
|||
Рис. 3.3. Элемент задержки |
A = B ={a1 ,..., an }. В качестве |
|||
множества состояний возьмём то же |
||||
множество: Q ={a1 ,..., an }. Тогда полагаем: ϕ(q,a) = a Q, ψ(q,a) = q B. Здесь текущее
состояние “запоминает” поступившую букву входного алфавита, а выходной буквой является предыдущее состояние, т.е. “запомненная” буква.
Автоматы V = ( A,Q, B,ϕ,ψ), определённые в этом параграфе,
называются автоматами Мили. Определим теперь автомат Мура,
или автомат без выхода.
Определение. Автоматом Мура называется тройка V = ( A,Q,ϕ), где A,Q − множества, а ϕ : Q × A → Q − отображение.
Множества A и Q называются соответственно входным алфавитом и множеством состояний. Предполагается, что множества A и Q конечны, хотя во многих вопросах это не имеет значения. Функция ϕ называется функцией переходов. Равенство ϕ(q,a) = q' означает, что если автомат находится в состоянии q и принимает символ а, то должен осуществиться его переход в состояние q'.
Покажем, что на самом деле в автомате Мили можно “избавиться” от выходного алфавита В, увеличив соответствующим образом множество состояний Q,
смысле подходящему автомату Мура. Пусть дан автомат Мили
V = ( A,Q, B,ϕ,ψ). Построим автомат Мура V ' = ( A',Q',ϕ'). В качестве множества состояний нового автомата возьмём Q' = Q × B, входной алфавит сохраним прежним: A' = A, а функцию ϕ'
определим следующим образом:
ϕ' (q',a) = ϕ'((q,b),a) = (ϕ(q,a),ψ(q,a)).
Автомат Мура V ' = ( A',Q',ϕ') эквивалентен автомату Мили
V = ( A,Q, B,ϕ,ψ) в том смысле, что V ' “работает” так же, как V ,
но реакцией на входной сигнал является не выходной символ b, а изменённое более сложным образом состояние, в котором фактически “зашифрован” выходной символ b.
§3.2. Диаграмма Мура и таблица автомата
Наряду с каноническими уравнениями работа автомата может быть описана с помощью диаграммы Мура или таблицы.
Определение. Диаграммой Мура автомата V = ( A,Q, B,ϕ,ψ)
называется ориентированный граф, вершинами которого являются
состояния q Q и для каждого равенства вида ϕ(a,q) = q' |
граф |
имеет ребро, идущее из q в q' , на котором стоит метка a,b, |
где |
b = ψ(q,a). |
|
|
|
0,a |
|
|
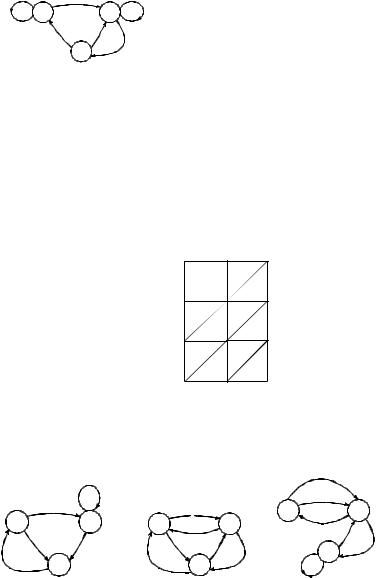
Например, следующей диаграммой |
||
1,b |
q1 |
q2 |
1,c |
Мура (см. рис. 3.4) изображается |
|||
|
|||||||
|
0,b |
|
1,c |
|
автомат, у которого A = {0,1}, |
||
|
q3 |
0,a |
B = {a,b,c}, Q = {q1 ,q2 ,q3}, |
||||
|
|
|
|||||
|
Рис. 3.4 |
|
|
ϕ(q1 ,0) = q2 , ϕ(q1 ,1) = q1 , |
|||
|
|
|
ψ(q1 |
,0) = a, ψ(q1 ,1) = b, |
|||
|
|
|
|
|
|||
Определение. Таблицей автомата V |
= ( A,Q, B,ϕ,ψ) называется |
||||||
прямоугольная таблица с n =|Q| строками и m =| A| столбцами, причём в клетке, стоящей на пересечении i -й строчки и j -го столбца
написаны символы ϕ(qi ,a j ) и ψ(qi ,a j ).
Например, автомат из предыдущего примера может задаваться таблицей
|
|
|
Табл. 3.1 |
|
|
0 |
|
1 |
|
q1 |
q2 |
a |
q1 |
b |
|
|
|||
|
|
|
||
q2 |
q3 |
a |
q2 |
c |
|
|
|
||
q3 |
|
|
|
|
Примеры решения задач
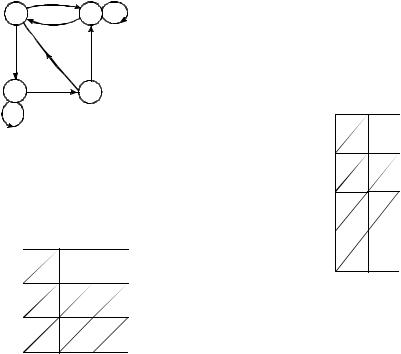
Задача 1. Выяснить, является ли следующий граф диаграммой Мура некоторого автомата:
|
|
|
|
|
|
|
|
a,a |
|
|
0,1 |
1,1 |
|
|
a,0 |
|
q1 |
b,a |
q2 |
|
|
|
|
a,a |
|||||
|
|
|
|
|
|||||
q1 |
q2 |
|
|
q1 b,1 |
q2 |
|
|
||
|
|
|
|
b,a |
|||||
|
0,0 |
|
|
|
|
a,1 |
|
q3 |
|
1,0 |
|
|
b,1 |
q3 |
|
b,b |
|||
0,1 |
q3 |
|
b,0 |
|
b,0 |
a,b |
|
|
|
|
|
|
|
|
|
|
|||
|
(а) |
|
|
|
(б) |
|
|
(в) |
|
|
|
|
|
Рис. 3.5 |
|
|
|
|
|
Решение. |
Граф (а) не является диаграммой Мура никакого автомата, |
|||||||||||
так как на диаграмме не указано, в какое состояние должен переходить |
||||||||||||
автомат, если он находится в состоянии q3 и получает на входе символ |
||||||||||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
Граф (б) также не является диаграммой Мура, так как переход из |
|
|
||||||||||
состояния |
q2 при получении символа b определён неоднозначно. |
|
||||||||||
Граф (в) является диаграммой Мура конечного автомата. |
|
|
|
|
|
|||||||
Из определения конечного автомата и диаграммы Мура следует, что |
|
|||||||||||
ориентированный граф, рёбра которого помечены символами a,b |
|
|
||||||||||
( a A,b B), |
является диаграммой Мура некоторого конечного |
|
||||||||||
автомата в том и только том случае, если из каждого состояния |
qi |
|
|
|||||||||
выходит по одной стрелке для каждого символа a A. |
|
|
|
|
|
|||||||
|
a,0 |
|
|
Задача 2. Построить таблицу автомата, |
||||||||
q1 |
q2 |
b,0 |
заданного следующей диаграммой Мура |
|||||||||
a,1 |
||||||||||||
(рис. 3.6): |
ϕ(q1 ,a) = q2 и |
|
||||||||||
b,0 |
|
a,1 |
b,1 |
|
Решение. Так как |
|
||||||
|
|
ψ(q1 ,a) = 0, то в клетке (q1 ,a) |
надо |
|||||||||
q3 |
|
|
q4 |
|
записать символы |
|
|
|
Табл. 3.2 |
|||
|
|
|
q2 и 0. Аналогично |
|
|
|||||||
a,1 |
|
|
a |
b |
||||||||
|
|
|
|
|||||||||
|
b,0 |
|
|
|
заполняются другие |
q1 |
q2 |
|
q3 |
|
||
|
Рис. 3.6 |
|
клетки таблицы, и |
|
0 |
0 |
||||||
|
|
|
мы получаем: |
|
|
|
|
|||||
Задача 3. |
Построить диаграмму Мура автомата, |
|
q2 |
q1 |
1 |
q2 |
0 |
|||||
заданного таблицей. |
|
|
|
|
|
|
||||||
|
|
|
q3 |
q4 |
|
q3 |
|
|||||
|
|
|
Табл. 3.3 |
|
Решение. Первая клетка |
1 |
0 |
|||||
|
|
|
|
|
|
|
||||||
|
0 |
1 |
2 |
|
показывает, что автомат, |
|
q1 |
|
q2 |
|
||
|
|
находясь в состоянии |
q |
q4 |
|
|
||||||
q1 |
q3 |
q1 |
q2 |
|
и приняв символ 0, |
1 |
|
|
1 |
|
1 |
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|||
|
|
должен перейти в |
|
|
|
|
|
|
||||
|
q2 0 |
q2 0 |
q3 1 |
|
|
|
|
|
|
|
||
q2 |
|
состояние q3 и выдать на выход символ 2. |
||||||||||
q3 |
q3 |
q3 |
q1 |
|
Следовательно, из q1 в q3 должно идти |
|||||||
|
1 |
2 |
0 |
|
|
|
|
|
|
|
|
|
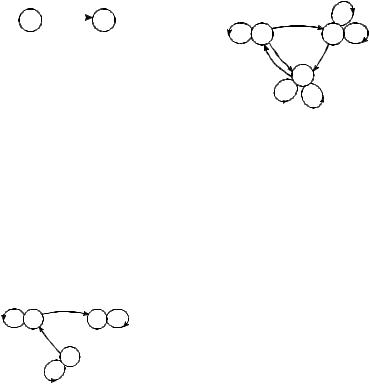
ребро, помеченное символами 0 и 2 (см. рис. 3.7).
|
0,2 |
|
q3 |
|
|
|
|
2,2 |
|
0,0 |
|||
|
q1 |
|
|
|
|
1,1 |
q1 |
|
q2 |
|
1,0 |
||
|
|
|
|
|
|
|
|||||||
|
|
Рис. 3.7 |
|
|
|
|
0,2 |
|
|||||
|
|
|
|
|
|
2,0 |
|
2,1 |
|
|
|||
|
Рассуждая |
аналогично |
для |
|
q3 |
|
|
||||||
|
|
|
|
|
|||||||||
других клеток, мы получаем |
|
|
|
1,2 |
|
|
|||||||
диаграмму |
Мура |
данного |
0,1 |
|
|
|
|||||||
автомата (см. рис. 3.8): |
|
|
|
|
|
|
|||||||
|
|
|
|
Рис. 3.8 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
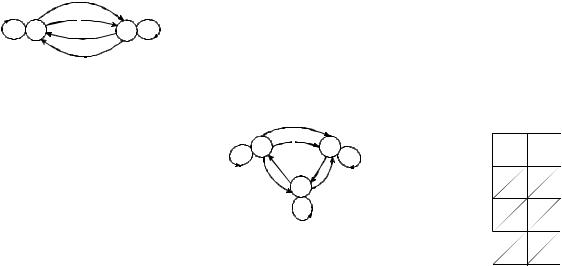
Задача 4. Автомат, у которого Q ={0, 1, 2}, |
A = B ={0, 1}, задан |
||||||||||||
каноническими уравнениями |
ϕ(q, a) = q + a (mod 3), |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ(q, a) = a , если q < 2, |
||||||
|
|
|
|
|
|
|
|
|
1 − a, если q = 2. |
||||
Построить диаграмму Мура этого автомата. |
|
|
|
|
|
|
|||||||
|
1,0 |
|
|
|
Решение. Пусть q = a = 0. Тогда |
||||||||
0,0 |
|
|
0,1 |
ϕ(q, a) = 0 и ψ(q, a) = 0. |
|
|
|||||||
0 |
|
|
1 |
|
|
||||||||
|
1,0 |
|
|
|
|
Следовательно, на диаграмме Мура |
|||||||
|
|
|
2 |
|
|
|
из кружочка, обозначающего |
|
|
||||
|
|
|
|
|
|
состояние 0, в этот же кружочек |
|
||||||
|
|
|
|
|
|
|
|
||||||
|
0,0 |
|
|
|
|
должна идти стрелка, помеченная |
|
||||||
|
|
|
|
|
символами 0, 0. Пусть теперь, |
|
|
||||||
|
|
Рис. 3.9 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
скажем, q = 2, |
a =1. Тогда |
|
|
|||
ϕ(q, a) = 2 +1 (mod3) = 0 и ψ(q, a) =1 − a = 0. Значит, из
кружочка с номером 2 в кружочек с номером 0 идёт стрелка, помеченная символами 0, 0. Рассматривая ана-логичным образом остальные случаи, получим диаграмму Мура (см. рис. 3.9).
Задачи для самостоятельного решения
1. |
Автомат V задан каноническими уравнениями |
|
|
b(t) |
= q(t) + a(t) (mod 3), |
|
|
= a(t) +1 (mod 3), |
|
q(t +1) |
|
где A = B = Q ={0, 1, 2}. Построить диаграмму Мура автомата V. |
||
2. |
Автомат V таков, что A ={0, 1}×{0, 1}, B = Q ={0, 1}, |
|
ϕ(q, (x, y)) = q + xy (mod 2), ψ(q, (x, y)) = q + x + y (mod 2).
a,a |
b,b |
a,c |
c,c |
||
0 |
b,c |
1 |
|
c,c |
|
|
Рис. 3.10. |
|
3. Написать канонические уравнения автомата, заданного следующей диаграммой Мура (см. рис. 3.11):
Ответы
1. См. рис. 3. 11. 2. См. табл. 3.
a(t), если q(t)
3. b(t) =
c, если a(t)
|
|
0,0 |
|
|
|
|
|
Табл. 3.3 |
|||
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
2,0 |
|
|
|
|
|
|
|
||
2,2 |
0 |
|
1 |
(0,0) |
0 |
|
1 |
|
|||
|
|
0 |
1 |
||||||||
|
|
2 |
|
2 |
|
|
0,1 |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
||
|
|
, |
1, |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
0 |
|
1 |
|
|
|
1 |
2 |
|
|
, |
2 |
(0,1) |
|
|
|
|
|
1 |
|
0 |
|
1 |
|
0 |
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
|
|
|
(1,0) |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
0 |
|
||
|
|
Рис. 3.11 |
|
|
(1,1) |
0 |
|
||||
=0,
=b или c.
§3.3. Продолжение функций ϕ и ψ
Пусть A ={a , a |
2 |
, ... a |
n |
} − конечный алфавит. Обозначим через A |
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
множество всех слов w = ai |
ai |
...ai . Число k называется длиной |
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
k |
|
|
|
слова w и обозначается |
|
| w | . Например, если A ={a,b, c}, |
то |
|
|
||||||||||
a, ab, babc A , | aba |= 3, |
| c |=1. Слово, в котором нет ни одной |
||||||||||||||
буквы, будем называть пустым словом и обозначать символом λ. |
|
||||||||||||||
Очевидно, |
| λ |= 0. |
Пусть Am − множество всех слов длины m, |
а |
|
|||||||||||
A+ − множество всех непустых слов. Полагаем A0 ={λ} . Очевидно, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
∞ |
|
|
∞ |
|
|
|
A+ = A \ {λ}, A = UAm , A+ = UAm . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
m=0 |
|
|
m=1 |
|
|
|
|
Произведением двух слов w, w′ A называется слово, полученное |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
приписыванием к слову w справа слова w . Таким образом, если |
|
|
|||||||||||||
w = ai |
ai |
...ai |
s |
, w′ = a j a j |
2 |
...a j , то |
|
|
|
||||||
1 |
2 |
|
|
|
|
|
|
1 |
|
t |
|
|
|
||
ww′ = ai ai ...ai |
|
a j a j |
...a j |
. Нетрудно проверить, что |
|
|
|
||||||||
|
1 |
2 |
|
|
s |
1 |
2 |
|
t |
|
|
|
|
||
произведение слов ассоциативно, т.е. (w1w2 )w3 = w1 (w2 w3 ) для |
|
||||||||||||||
любых |
w , w , w A . Вообще, произведение слов w w ... w |
s |
|||||||||||||
|
1 |
2 |
|
|
3 |
|
|
|
|
|
1 |
2 |
|
||
не зависит от расстановки скобок (но зависит от порядка сомножителей). В частности,
((w1w2 )w3 )w4 = (w1 (w2 w3 ))w4 = (w1w2 )(w3 w4 ) = = w1 ((w2 w3 )w4 ) = w1 (w2 (w3 w4 )).
Произведение слов некоммутативно, так как в общем случае
w1w2 = w2 w1.
Множество, на котором задана ассоциативная операция, называется полугруппой. Полугруппа S, в которой есть единица, т.е. такой
элемент е, что ae = ea = a для всех a A, называется моноидом.
Множества A и A+ являются полугруппами. Кроме того, A − моноид (так как wλ = λw = w для всех w A , то пустое слово λ
является единицей). Полугруппа A+ моноидом не является. Действительно, если ae = a при некоторых a, e A , то
| a |=| ae |=| a | + | e | , откуда | e |= 0 , что невозможно, так как e ≠ λ . Функции ϕ : Q × A → Q и ψ : Q × A → B можно продолжить до
функций ϕ : Q × A → Q и ψ : Q × A → B следующим образом. Положим
ϕ(q, a) = ϕ(q, a) при a A,
ϕ(q, aw) = ϕ(ϕ(q, a), w) при a A, w A+ ; ψ(q, a) =ψ(q, a) при a A,
ψ(q, aw) =ψ(q, a)ψ(ϕ(q, a), w) при a A, w A+ ; ϕ(q, λ) = q, ψ(q, λ) = λ.
Функция ϕ несёт информацию о том, в какое состояние перейдёт автомат, если на его вход будут поступать последовательно несколько букв из алфавита A. Действительно, если в какой-либо момент автомат находится в состоянии q, а на его вход поступают буквы
ai1 , ai2 , ... ais , то будут осуществляться следующие переходы в
другие состояния:
q →ϕ(q, ai1 ) →ϕ(ϕ(q, ai1 ), ai2 ) → . .. → →ϕ(ϕ(.. .ϕ(q, ai1 ), ai2 ), ... ais ),
т.е. в конце концов автомат окажется в состоянии ϕ(q, ai1 ... ais ).
Аналогичным образом интерпретируется функция ψ. А именно,
|
ψ |
(q, ai |
... ai |
) = b j |
b j |
2 |
... b j |
s |
, |
где b j |
k |
− буква, которая будет |
1 |
s |
1 |
|
|
|
|
|
|||||
выдана автоматом на k -м шаге.
Примеры решения задач
Пример 1. Автомат задан таблицей 3.4.
Определить: ϕ(q1, ab), ϕ(q2 , abc), |
|
a |
|
|
Табл. 3.4 |
|||
ϕ(q1, abca), ψ(q1,ba), ψ(q2 , a3b2 ). |
|
|
b |
c |
||||
Решение. |
|
|
|
q1 |
q1 |
0 |
q2 |
q2 |
|
|
|
|
|
0 |
1 |
||
ϕ(q1, ab) = ϕ(ϕ(q1, a),b) = ϕ(q1,b) = q2 ; |
|
|||||||
q1 |
|
q1 1 |
q2 1 |
|||||
ϕ(q2 , abc) =ϕ(ϕ(q2 , a), bc) =ϕ(q1 , bc) = |
q2 |
0 |
||||||
ϕ(ϕ(q1 ,b), c) = ϕ(q2 , c) = q2 ; |
|
|
|
|
|
|
||
a |
b |
c |
a |
, |
|
|
|
|
q1 →q1 |
→q2 |
→q2 |
→q1 |
|
|
|
|
|
поэтому
ϕ(q1, abca) = q1;
ψ(q1,ba) =ψ(q1,b)ψ(ϕ(q1,b), a) = 0ψ(q2 , a) = 00; q2 a→q1 a→q1 a→q1 b→q2 b→q1,
0 |
0 |
0 |
0 |
1 |
поэтому ψ(q2 , a3b2 ) = 00001.
Пример 2. Автомат задан диаграммой Мура, изображенной на рис. 3.12. Найти:
ϕ(q1, 001), ψ(q3 ,110).
Решение. Имеем:
q1 0→q2 0→q1 1→q2 ,
поэтому ϕ(q1, 001) = q2 ;
0,0
 q1
q1
 1,0
1,0 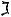
 q2
q2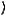
0,1 
 0,2 1,0
0,2 1,0
q3 |
|
q4 |
1,2 |
|
1,1 |
||||
|
|
|
||
|
Рис. 3.12 |
|
||
ψ(q3 ,110) =ψ(q3 ,1)ψ(ϕ(q3 ,1),1)ψ(ϕ(ϕ(q3 ,1),1), 0) =
=1ψ(q4 ,1)ψ(ϕ(q4 ,1), 0) =12ψ(q4 , 0) =121.
