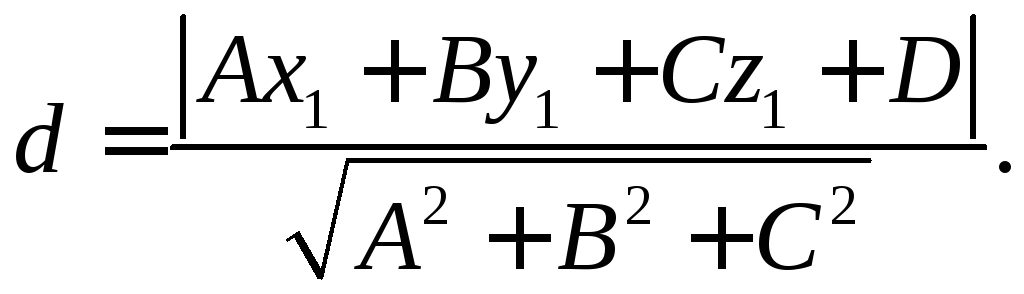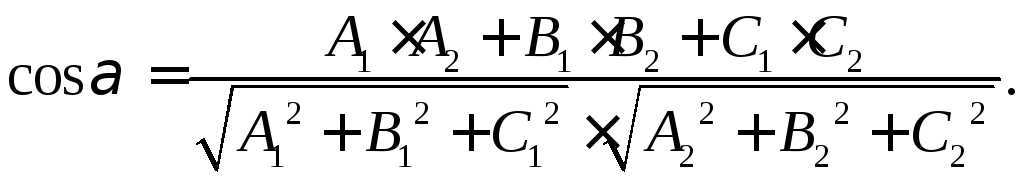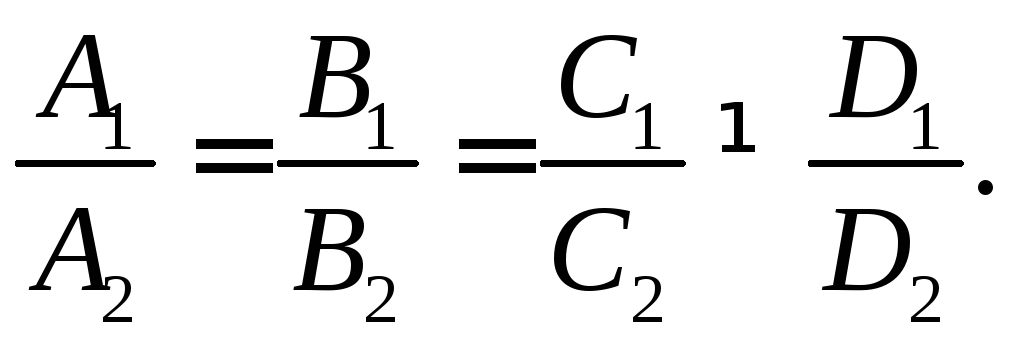- •1 Курс, 1 семестр.
- •Лекция 1. Определители. (рассм. На прк)
- •Свойства определителей (справедливы для определителей любого порядка)
- •Вычисление определителей 4-го и более высоких порядков.
- •Лекция 3. Скалярное, векторное и смешанное произведение векторов и их свойства.
- •Лекция 4. Комплексные числа
- •Линейная алгебра
- •Лекция 5. Матрицы: определения, виды матриц.
- •Действия над матрицами.
- •Основные определения
- •Линейные операции над матрицами
- •Транспонирование матриц и его свойства
- •Лекция 6. Системы линейных алгебраических уравнений и методы их решения (формулы Крамера, матричный метод)
- •Решение систем трех линейных уравнений с тремя неизвестными матричным методом.
- •Лекция 7. Решение систем линейных алгебраических уравнений (слау) методом Гаусса Суть метода Гаусса:
- •Решение однородных слау
- •Лекция 8. Плоскость в пространстве
- •1.1. Общее уравнение плоскости в пространстве
- •1.2. Уравнение плоскости, проходящей через данную точку параллельно двум заданным (неколлинеарным) векторам
- •1.3. Уравнение плоскости, проходящей через три данные точки
- •1.4. Уравнение плоскости «в отрезках»
- •1.5. Нормальное уравнение плоскости
- •1.6. Полярные параметры плоскости
- •1.7. Особые случаи расположения плоскости в пространстве относительно системы координат
- •2. Плоскости в пространстве: взаимное расположение
- •2.5. Угол между плоскостями
- •2.6. Условия параллельности и перпендикулярности плоскостей
- •1.1. Уравнение прямой на плоскости,
- •1.10. Полярные параметры прямой
- •2. Прямые на плоскости: взаимное расположение
- •2.1. Условие, при котором три точки лежат на одной прямой
- •2.2. Взаимное расположение прямой и пары точек
- •2.3. Расстояние от точки до прямой
- •2.4. Пучок прямых
- •2.5. Угол между прямыми
- •2.6. Условия параллельности и перпендикулярности прямых
- •2.7. Точка пересечения непараллельных прямых
- •Лекция 10. Прямая в пространстве
- •Лекция 11. Кривые второго порядка
- •Лекция 12. Поверхности второго порядка
- •Математический анализ
2. Плоскости в пространстве: взаимное расположение
2.1. Условие, при котором четыре точки лежат в одной плоскости
Четыре точки
пространства –
![]() ,
,![]() ,
,![]() ,
,![]() – лежат в одной плоскости тогда и только
тогда, когда векторы
– лежат в одной плоскости тогда и только
тогда, когда векторы![]() компланарны, т.е. выполнено условие:
компланарны, т.е. выполнено условие:

Равенство нулю
определителя (12) означает, что объем
параллелепипеда, построенного на
векторах
![]() ,
равен нулю.
,
равен нулю.
2.2. Взаимное расположение плоскости и пары точек
Взаимное расположение
точек
![]()
![]() и плоскости
и плоскости![]() можно
определить по следующим признакам:
можно
определить по следующим признакам:
1) выражения
![]() и
и![]() имеют одинаковые знаки, в этом случае
точки
имеют одинаковые знаки, в этом случае
точки![]() и
и![]() лежат по одну сторону от плоскости;
лежат по одну сторону от плоскости;
2) числа
![]() и
и![]() ,
определенные в п. 1, имеют противоположные
знаки, в этом случае точки
,
определенные в п. 1, имеют противоположные
знаки, в этом случае точки![]() и
и![]() лежат по разные стороны от плоскости
(отрезок
лежат по разные стороны от плоскости
(отрезок![]() пересекает плоскость);
пересекает плоскость);
3) одно из чисел
![]() ,
,![]() равно нулю или они оба равны нулю, в этом
случае одна из точек
равно нулю или они оба равны нулю, в этом
случае одна из точек![]() ,
,![]() соответственно или обе точки принадлежат
плоскости.
соответственно или обе точки принадлежат
плоскости.
2.3. Расстояние от точки до плоскости
|
|
Расстояние d
от точки
|
2.4. Пучок плоскостей
Через одну
фиксированную прямую
![]() в пространстве (рис. 19) проходит бесконечное
множество плоскостей. Это множество
называетсяпучком
плоскостей,
а прямая
в пространстве (рис. 19) проходит бесконечное
множество плоскостей. Это множество
называетсяпучком
плоскостей,
а прямая
![]() –осью
пучка.
–осью
пучка.
|
Рис. 19 |
Если пара
различных плоскостей –
|
![]()
![]()
которое называется уравнением пучка плоскостей.
Замечание.
Уравнение (14) также задает плоскости
![]() и
и![]() Например, при
Например, при![]() получим уравнение плоскости
получим уравнение плоскости![]() ,
а при
,
а при![]() – уравнение плоскости
– уравнение плоскости![]() .
.
2.5. Угол между плоскостями
|
Если пара
плоскостей в пространстве (рис. 20)
задана общими уравнениями:
|
Рис. 20 |
Замечание.
Углом между
плоскостями принято считать тот из
образованных ими двугранных углов,
который является острым. Обозначим
значение выражения, полученного по
формуле (15) через
![]() .
Тогда при
.
Тогда при![]() угол между плоскостями равен
угол между плоскостями равен![]() ,
а при
,
а при![]() – (
– (![]() ).
).
2.6. Условия параллельности и перпендикулярности плоскостей
Утверждение 2.
Пусть в
пространстве заданы две плоскости:
![]() и
и![]() .
Тогда выполняется одно и только одно
из трех условий:
.
Тогда выполняется одно и только одно
из трех условий:
1) плоскости не
имеют общих точек
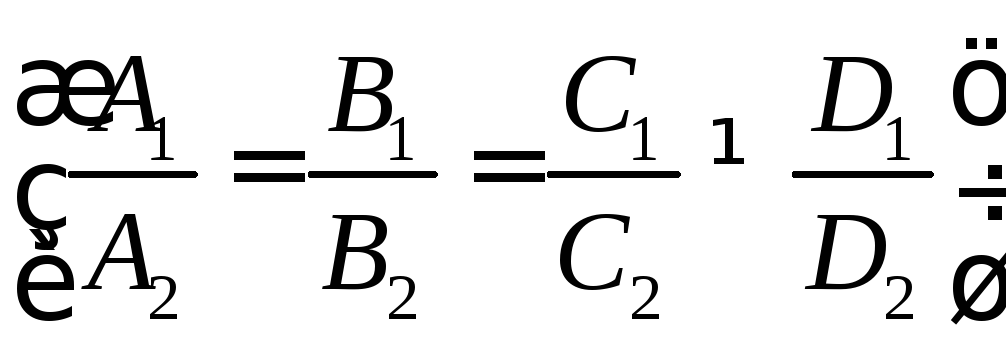 ;
;
2) плоскости
пересекаются по прямой
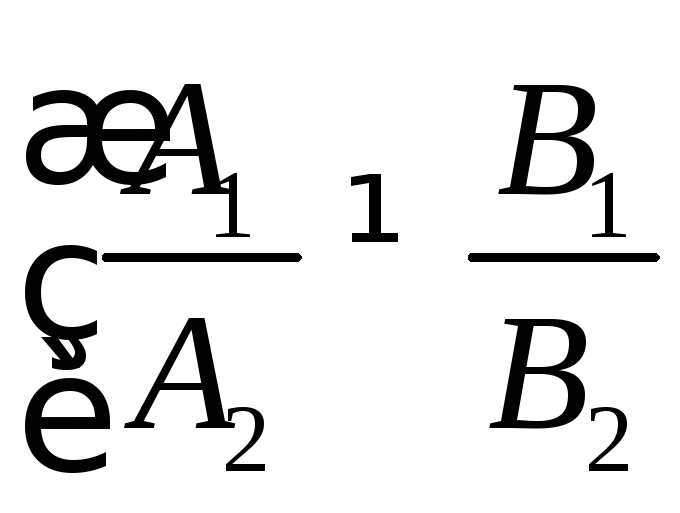 или
или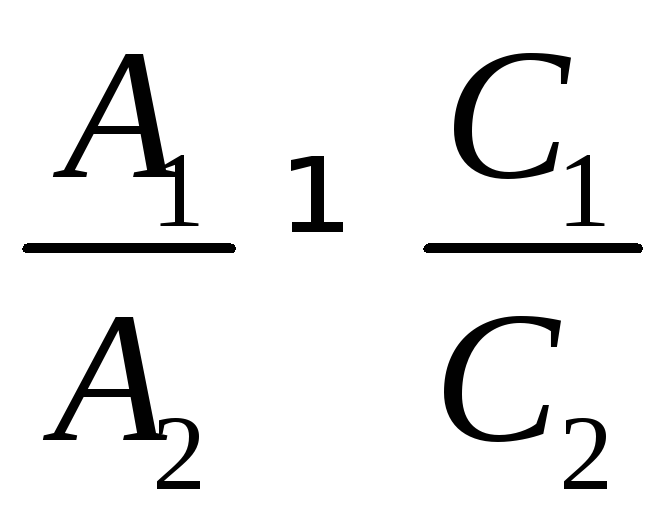 ,
или
,
или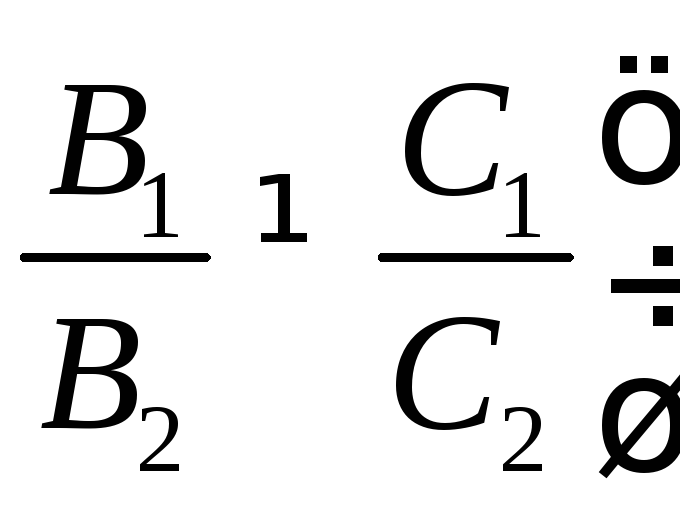 ;
;
3) плоскости
совпадают
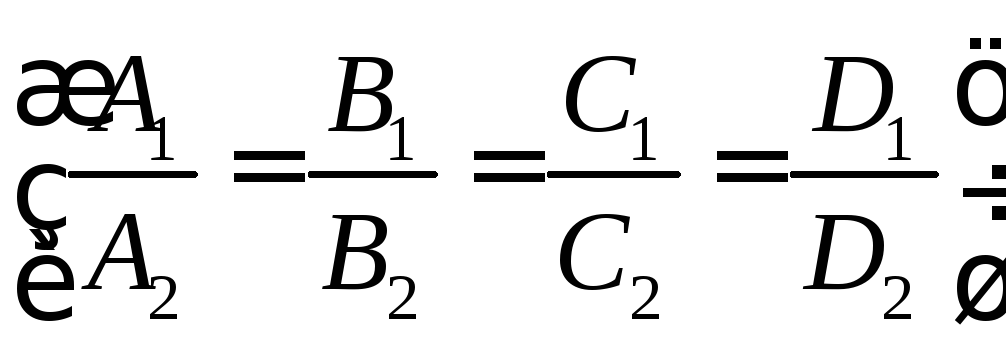 .
.
Пусть плоскости
![]() и
и![]() заданы общими уравнениями
заданы общими уравнениями![]() и
и![]() соответственно. Очевидно, что
рассматриваемые плоскости (рис. 21)
параллельны в том, и только в том случае,
если параллельны (коллинеарны) их
нормальные векторы. Так как плоскость
соответственно. Очевидно, что
рассматриваемые плоскости (рис. 21)
параллельны в том, и только в том случае,
если параллельны (коллинеарны) их
нормальные векторы. Так как плоскость![]() имеет нормальный вектор
имеет нормальный вектор![]() ,
а плоскость
,
а плоскость![]() –
–![]() ,
то условие коллинеарности векторов
соответствует условию:
,
то условие коллинеарности векторов
соответствует условию:![]() (для некоторого коэффициента
пропорциональности
(для некоторого коэффициента
пропорциональности![]() ).
Для
).
Для
|
Рис. 21 |
векторов, заданных
координатами, это означает
пропорциональность соответст-вующих
координат. Таким образом, сог-ласно
утверждению 2 несовпадающие плоскости
|
Замечание.
Если для плоскостей
![]() и
и![]() выполняется условие
выполняется условие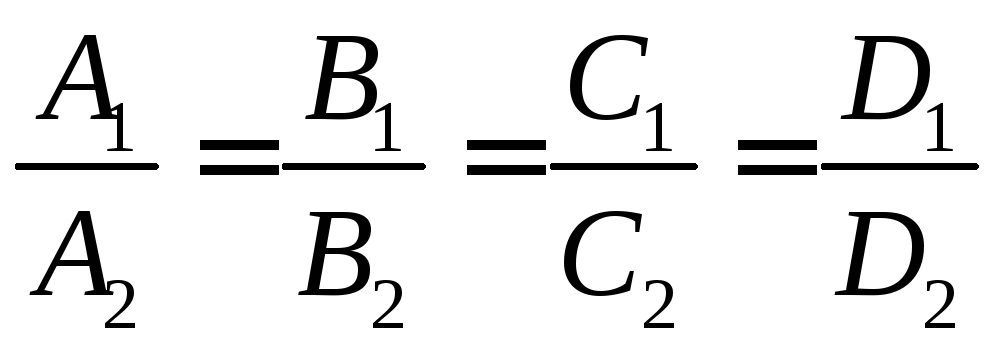 ,
то уравнения
,
то уравнения![]() и
и![]()
![]() задают в пространстве одну и ту же
плоскость, представленную различными
уравнениями, причем одно из уравнений
легко получить из другого умножением
его на соответствующий множитель.
задают в пространстве одну и ту же
плоскость, представленную различными
уравнениями, причем одно из уравнений
легко получить из другого умножением
его на соответствующий множитель.
|
Рис. 22 |
Если нарушается
хотя бы одно из равенств в условии
(16), то согласно ут-верждению 2 плоскости
|
гональность) их нормальных векторов, что соответствует равенству нулю их скалярного произведения. Таким образом, условие перпендикулярности плоскостей можно записать так:
![]()
![]()
Лекция 9. Прямая на плоскости (изучить самостоятельно)
ПРЯМАЯ НА ПЛОСКОСТИ: ВИДЫ УРАВНЕНИЙ

 Рис. 18
Рис. 18