
- •1 Курс, 1 семестр.
- •Лекция 1. Определители. (рассм. На прк)
- •Свойства определителей (справедливы для определителей любого порядка)
- •Вычисление определителей 4-го и более высоких порядков.
- •Лекция 3. Скалярное, векторное и смешанное произведение векторов и их свойства.
- •Лекция 4. Комплексные числа
- •Линейная алгебра
- •Лекция 5. Матрицы: определения, виды матриц.
- •Действия над матрицами.
- •Основные определения
- •Линейные операции над матрицами
- •Транспонирование матриц и его свойства
- •Лекция 6. Системы линейных алгебраических уравнений и методы их решения (формулы Крамера, матричный метод)
- •Решение систем трех линейных уравнений с тремя неизвестными матричным методом.
- •Лекция 7. Решение систем линейных алгебраических уравнений (слау) методом Гаусса Суть метода Гаусса:
- •Решение однородных слау
- •Лекция 8. Плоскость в пространстве
- •1.1. Общее уравнение плоскости в пространстве
- •1.2. Уравнение плоскости, проходящей через данную точку параллельно двум заданным (неколлинеарным) векторам
- •1.3. Уравнение плоскости, проходящей через три данные точки
- •1.4. Уравнение плоскости «в отрезках»
- •1.5. Нормальное уравнение плоскости
- •1.6. Полярные параметры плоскости
- •1.7. Особые случаи расположения плоскости в пространстве относительно системы координат
- •2. Плоскости в пространстве: взаимное расположение
- •2.5. Угол между плоскостями
- •2.6. Условия параллельности и перпендикулярности плоскостей
- •1.1. Уравнение прямой на плоскости,
- •1.10. Полярные параметры прямой
- •2. Прямые на плоскости: взаимное расположение
- •2.1. Условие, при котором три точки лежат на одной прямой
- •2.2. Взаимное расположение прямой и пары точек
- •2.3. Расстояние от точки до прямой
- •2.4. Пучок прямых
- •2.5. Угол между прямыми
- •2.6. Условия параллельности и перпендикулярности прямых
- •2.7. Точка пересечения непараллельных прямых
- •Лекция 10. Прямая в пространстве
- •Лекция 11. Кривые второго порядка
- •Лекция 12. Поверхности второго порядка
- •Математический анализ
Лекции по высшей математике
1 Курс, 1 семестр.
Линейная алгебра
Лекция 1. Определители. (рассм. На прк)
Определителем второго порядка называется выражение:
 ,
равное a11a22-a12a21
,
равное a11a22-a12a21
Определителем третьего порядка называется выражение:
 ,
равное
a11a22a33+a12a23a31+a12a21a32-a13a22a31-a12a21a33-a11a23a32
,
равное
a11a22a33+a12a23a31+a12a21a32-a13a22a31-a12a21a33-a11a23a32


Мнемоническое правило вычисления определителей (только третьего порядка)
+ -








Свойства определителей (справедливы для определителей любого порядка)
Определитель не меняется от замены строк столбцами (и наоборот)
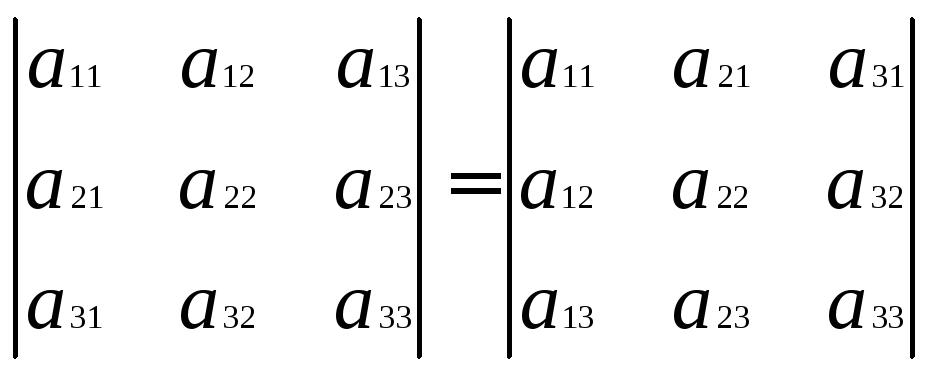
Если переставить две соседние строчки определителя, то он поменяет знак
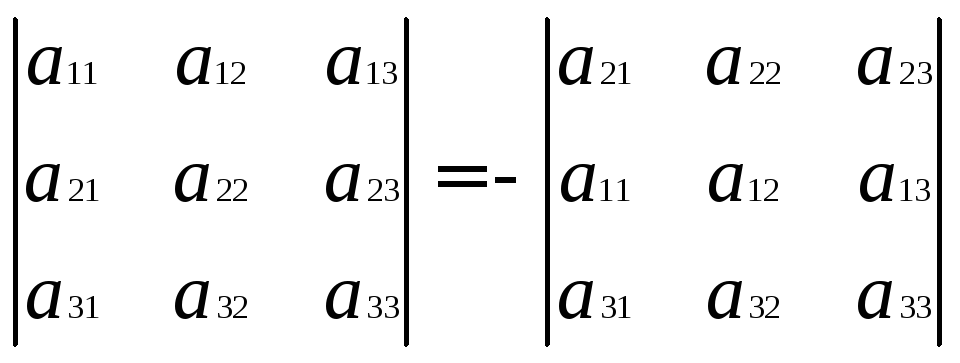
Если у определителя две одинаковые строчки или столбца, то он равен 0

Если элементы строки или столбца умножить на k, то соответствующий определитель умножится на k

Если все элементы некоторой строчки или столбца равны 0, то определитель равен 0
Если элементы строчек или столбцов пропорциональны, то определитель равен 0

Если элементы строчки или столбца представлены в виде суммы aij+bij, то определитель можно представить в виде суммы двух, в соответствующей строчке (столбце) одного из них будет стоять aij, а другого – bij
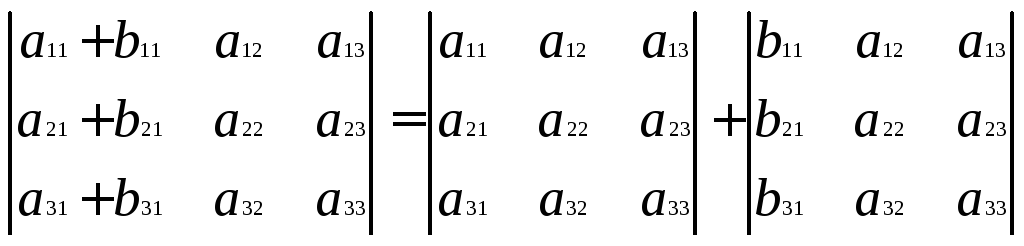
Если к какой-либо строчке или столбцу определителя прибавить другую строчку или столбец определителя, умноженную на k, то определитель от этого не изменится

Определитель можно разложить по строчке или столбцу:
Минором Mij определителя n-го порядка называется определитель порядка n-1, получающийся вычеркиванием i-той строчки и j-того столбца.
 ,
,

Алгебраическим дополнением Aij называют выражение Aij=(-1)i+jMij. Знаки алгебраических дополнений:

Разложение определителя по строке или столбцу:

Более подробно эта формула запишется в таком виде (это разложение по первой строке):

Вычисление определителей 4-го и более высоких порядков.
Для вычисления определителей порядка выше третьего используется метод разложения определителя по строке или столбцу, который позволяет понизить порядок вычисляемых определителей. Понизив порядок определителей до 3-го (или 2-го) используют описанные выше способы их вычисления.
Задача.
Вычислить определитель 4-го порядка
 .
.
Решение. Сначала найдем в заданном определителе такую строку (или столбец), в которой содержится наибольшее число нулевых элементов. В данной задаче это четвертая строка (или четвертый столбец). Для определенности будем проводить разложение по четвертой строке, образуем сумму, состоящую из произведений элементов этой строки на соответствующее алгебраическое дополнение.
Вычислим миноры нужных элементов.


Соответствующие
алгебраические дополнения:
![]() ,
,![]()
Вычислим данный
определитель:
![]()
![]()
Замечание. Вычисление определителя, например, 6-го порядка, сначала сводится к вычислению определителей 5-го порядка, которые затем сводятся к определителям 4го порядка, каждый из которых вычисляется как показано выше. Таким образом, можно вычислять определители любого (конечного) порядка.
Векторная алгебра.
Лекция 2. Понятие геометрического вектора. Проекции координат вектора. Направляющие косинусы вектора. Операции над геометрическими векторами. Разложение вектора по базису.
Коллинеарность и компланарность векторов.
1.Понятие геометрического вектора.
Под геометрическим
вектором
![]() мы
будем понимать совокупность равных и
одинаково направленных отрезков.
Геометрический вектор однозначно
определяется заданием его длины и
направления на плоскости –R2
– или в пространстве – R3.
мы
будем понимать совокупность равных и
одинаково направленных отрезков.
Геометрический вектор однозначно
определяется заданием его длины и
направления на плоскости –R2
– или в пространстве – R3.
2.Проекция вектора на ось
 Проекцией
вектора
Проекцией
вектора![]() на
осьOx
называется вектор
на
осьOx
называется вектор
![]() ,
который сонаправлен с осьюOx
или
противоположно направлен ей и имеет
длину
,
который сонаправлен с осьюOx
или
противоположно направлен ей и имеет
длину
![]() ,
где
,
где![]() - угол между направлением вектора
- угол между направлением вектора![]() и
осьюOx.
и
осьюOx.

![]()
![]()
3.Длина и направляющие косинусы вектора
 Проекции вектора
Проекции вектора
![]() на
оси системы координат можно задать
двумя способами.
на
оси системы координат можно задать
двумя способами.
 - координатами.
- координатами.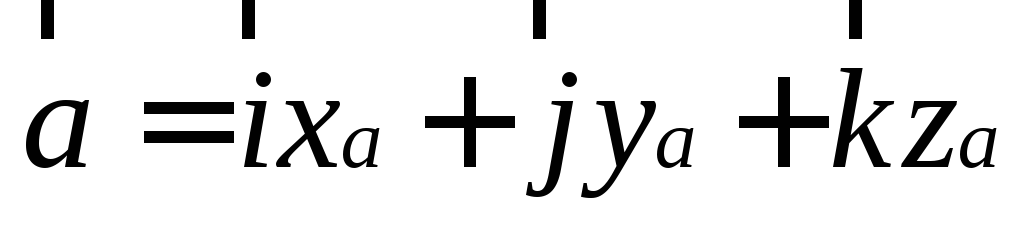 - в
виде разложения вектора по ортам системы
координат.
- в
виде разложения вектора по ортам системы
координат.
В ектор
ектор![]() имеет длину
имеет длину![]()
Под направляющими
косинусами
мы будем понимать косинусы углов между
осями системы координат и направлением
данного вектора.
![]() -
угол между осьюOx
и направлением вектора,
-
угол между осьюOx
и направлением вектора,
![]() -
угол между осьюOy
и направлением вектора,
-
угол между осьюOy
и направлением вектора,
![]() -
угол между осьюOz
и направлением
вектора.
-
угол между осьюOz
и направлением
вектора.



Для направляющих
косинусов выполняется тождество
![]() .
Действительно, подставив вместо
.
Действительно, подставив вместо![]() ,
,![]() и
и![]() их определения через отношение
соответствующей проекции вектора к его
длине, получим:
их определения через отношение
соответствующей проекции вектора к его
длине, получим:



Понятие направляющих
косинусов тесно связано с понятием орта
вектора. Вектор
![]() будем называть ортом вектора
будем называть ортом вектора![]() ,
если он имеет единичную длину и такое
же направление, что и вектор
,
если он имеет единичную длину и такое
же направление, что и вектор![]() .
.
![]()
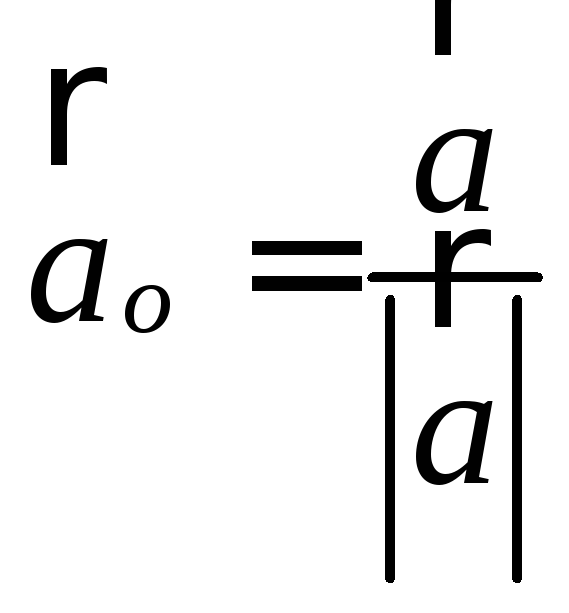
4.Операции над геометрическими векторами
Вектор
![]() ,
начало которого совпадает с концом,
будем называть нулевым.
,
начало которого совпадает с концом,
будем называть нулевым.
Вектор
![]() ,
имеющий ту же длину, что и
,
имеющий ту же длину, что и![]() и противоположно ему направленный,
будем называть противоположным вектором.
и противоположно ему направленный,
будем называть противоположным вектором.
Умножение вектора на число.

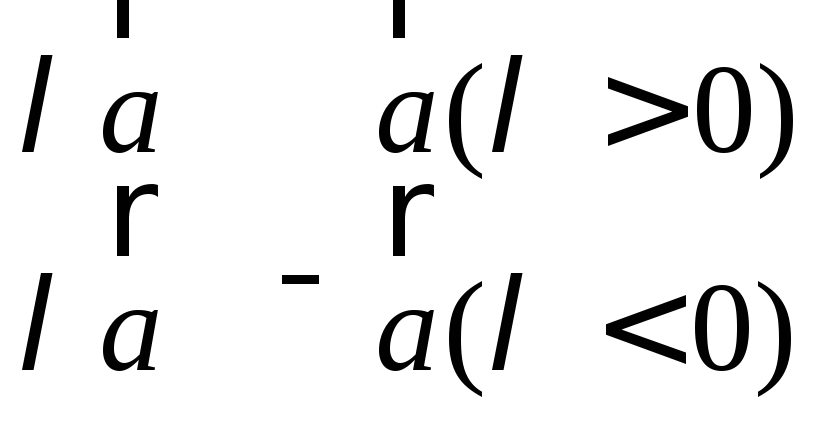
При умножении вектора на число нужно все его координаты умножить на это число:
![]()
![]()
Сложение векторов.
Два вектора складываются по правилу треугольника или по правилу параллелограмма.
В координатах
сумма вектора
![]() и вектора
и вектора![]() имеет координаты
имеет координаты![]()
5. Свойства операций над векторами
5.1 Свойства умножения вектора на число:
5.2 Свойства сложения векторов:

 (коммутативность,
или перестановочность сложения)
(коммутативность,
или перестановочность сложения) (дистрибутивность
относительно числа)
(дистрибутивность
относительно числа) (дистрибутивность
относительно векторов)
(дистрибутивность
относительно векторов)
Множество всех векторов с вышеперечисленными свойствами называется векторным пространством.
6. Коллинеарность и компланарность векторов
6.1 Коллинеарность векторов
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных. Нулевой вектор коллинеарен любому вектору.
Условие коллинеарности векторов в координатах:

Два вектора в пространстве коллинеарны друг другу, если отношение их соответствующих координат постоянно.
6.2 Компланарность векторов
Три ненулевых вектора называются компланарными если они, будучи приведенными к одному началу, лежат в одной плоскости. Если хотя бы один из векторов нулевой, то вся тройка компланарна.
Необходимое и достаточное условие компланарности векторов с координатами
![]()
![]()
![]() записывается в
виде:
записывается в
виде:

Оно вытекает из свойств смешанного произведения векторов, которое будет рассмотрено далее.
7. Базисы R2 и R3. Разложение вектора по базису.
Два (три ) вектора называют базисными R2 (R3), если произвольный вектор из R2 (R3) можно разложить через базисные, а сами векторы друг через друга не выражаются.
Два неколлинеарных
вектора на плоскости образуют базис
R2.
В этом случае разложение вектора
![]() по
базису
по
базису![]() ,
,![]() можно представить в виде
можно представить в виде![]() ,
где
и
– коэффициенты разложения.
,
где
и
– коэффициенты разложения.
Тройка некомпланарных векторов образует базис R3.
Пример разложения
вектора
![]() по базису
по базису![]() ,
,![]() на
плоскости:
на
плоскости:
![]()
![]()
![]()
Проверяем неколлинеарность базисных векторов:
![]() ,
значит базисные вектора неколлинеарны
и возможно разложение единственным
образом.
,
значит базисные вектора неколлинеарны
и возможно разложение единственным
образом.
Представим вектор
 в виде
в виде ,
тогда можно написать:
,
тогда можно написать: ,
или в виде системы двух уравнений:
,
или в виде системы двух уравнений:
![]() ,
решая которую найдем =2,
.
Таким образом,
,
решая которую найдем =2,
.
Таким образом,
![]()
