1.1. Общее уравнение плоскости в пространстве

Зададим в пространстве декартову прямоугольную систему коорди-

нат (ДПСК). Пусть – фиксированная точка пространства,– ненулевой вектор. Тогдауравнение плоскости в пространстве, проходящей через точку перпендикулярно к векторуможет быть записанов векторной форме:

где векторы и– радиусы-векторы точек(произвольной точки этой плоскости) исоответственно (рис. 1). В этом случае векторназываютнормальным вектором данной плоскости или нормалью. Переписав уравнение (1) в координатной форме, получим:

Рис. 1

Раскроем скобки в левой части равенства (2) и введем обозначение: , тогда уравнение плоскости можно записать в виде:

Утверждение 1. Если в уравнении (3) хотя бы один из коэффициентов не равен нулю, то уравнение (3) в пространстве определяет некоторую плоскость. Уравнение вида (3) называетсяобщим уравнением плоскости в пространстве.

Замечание. Вывод уравнения (3) позволяет считать, что вектор с координатами является нормальным вектором плоскости, заданной общим уравнением:Например, если плоскость задана уравнениемто вектор нормали будет иметь координаты:.

1.2. Уравнение плоскости, проходящей через данную точку параллельно двум заданным (неколлинеарным) векторам

Пусть в пространстве заданы фиксированная точка и два неколлинеарных вектора –и. Рассмотрим плос- кость в пространстве, проходящую через данную точку параллельно заданным

Рис. 2

векторам. Если – произвольная точка плоскости, то векторы,икомпланарны (рис. 2). Условием компланарности трех векторов является равенство нулю их смешанного произведения, запишем это условие в координатной форме:

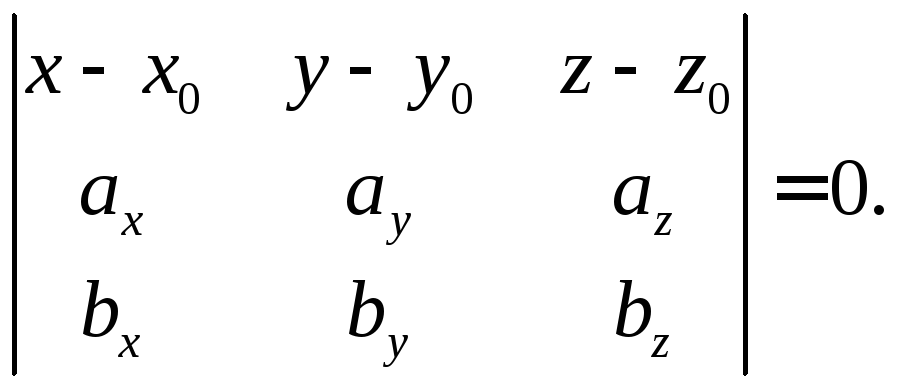
Из уравнения (4), раскрыв определитель и приведя подобные, получим общее уравнение плоскости, проходящей через данную точку параллельно двум неколлинеарным векторам. Уравнение вида (4) называютдетерминантным уравнением плоскости.

1.3. Уравнение плоскости, проходящей через три данные точки

Рассмотрим три фиксированные точки пространства (рис. 3), не лежащие на одной прямой, и запишем их координаты: ,,. Поскольку точки не лежат на одной прямой, то векторыи

Рис. 3

не являются коллинеарными. Таким образом, плоскость, проходящая через точки ,,совпадает с плоскостью, проходящей через точкупараллельно двум заданным (неколлинерным) векторам –

и . Если– произвольная точка рассматриваемой плоскости, то ее уравнение можно записать, пользуясь формулой (4). В качестве точкивозьмем точку(см. рис. 3), координаты векторовизаменим координатами векторовисоответственно и получим:

Таким образом, уравнение (5) является уравнением плоскости в прост-ранстве, проходящей через три данные точки, не лежащие на одной прямой.

1.4. Уравнение плоскости «в отрезках»

Пусть плоскость задана своим общим уравнением: . Предположим, что коэффициент. Перепишем данное уравнение плос-кости:разделим обе части полученного равенства наи получим уравнение плоскости в виде:

Введем следующие обозначения: ,,, тогда уравнение (6) примет вид, называемыйуравнением плоскости «в отрезках»:

Рассмотрим в пространстве декартову прямоугольную систему координат. Очевидно, что точки пространства с координатами ,,принадлежат плоскости, заданной уравнением (7). Следовательно, рассматриваемая плоскость отсекает на осях координат отрезки, значения длины которых соответствуют значениям параметров, взятым по модулю. При этом положительный знак параметра означает, что отрезок отсекается на положительной части соответствующей оси координат, а отрицательный – на отрицательной.

Пример. Записать уравнение плоскости «в отрезках» и построить данную плоскость в ДПСК.

Решение. Перенесем свободный член данного уравнения в его правую часть: После деления уравнения на 6 проведем соответствующие

Рис. 4

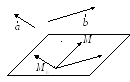
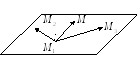
преобразования коэффициентов и получим: – это и есть требуемое уравнение плоскости«в отрезках». Схематичное изображение плоскости, которая отсекает на положительной части осиотрезок длиной 2, на отрицательной части оси– отрезок длиной 3, на положительной части оси– отрезок длиной 6, приведен на рис. 4.