
- •1 Курс, 1 семестр.
- •Лекция 1. Определители. (рассм. На прк)
- •Свойства определителей (справедливы для определителей любого порядка)
- •Вычисление определителей 4-го и более высоких порядков.
- •Лекция 3. Скалярное, векторное и смешанное произведение векторов и их свойства.
- •Лекция 4. Комплексные числа
- •Линейная алгебра
- •Лекция 5. Матрицы: определения, виды матриц.
- •Действия над матрицами.
- •Основные определения
- •Линейные операции над матрицами
- •Транспонирование матриц и его свойства
- •Лекция 6. Системы линейных алгебраических уравнений и методы их решения (формулы Крамера, матричный метод)
- •Решение систем трех линейных уравнений с тремя неизвестными матричным методом.
- •Лекция 7. Решение систем линейных алгебраических уравнений (слау) методом Гаусса Суть метода Гаусса:
- •Решение однородных слау
- •Лекция 8. Плоскость в пространстве
- •1.1. Общее уравнение плоскости в пространстве
- •1.2. Уравнение плоскости, проходящей через данную точку параллельно двум заданным (неколлинеарным) векторам
- •1.3. Уравнение плоскости, проходящей через три данные точки
- •1.4. Уравнение плоскости «в отрезках»
- •1.5. Нормальное уравнение плоскости
- •1.6. Полярные параметры плоскости
- •1.7. Особые случаи расположения плоскости в пространстве относительно системы координат
- •2. Плоскости в пространстве: взаимное расположение
- •2.5. Угол между плоскостями
- •2.6. Условия параллельности и перпендикулярности плоскостей
- •1.1. Уравнение прямой на плоскости,
- •1.10. Полярные параметры прямой
- •2. Прямые на плоскости: взаимное расположение
- •2.1. Условие, при котором три точки лежат на одной прямой
- •2.2. Взаимное расположение прямой и пары точек
- •2.3. Расстояние от точки до прямой
- •2.4. Пучок прямых
- •2.5. Угол между прямыми
- •2.6. Условия параллельности и перпендикулярности прямых
- •2.7. Точка пересечения непараллельных прямых
- •Лекция 10. Прямая в пространстве
- •Лекция 11. Кривые второго порядка
- •Лекция 12. Поверхности второго порядка
- •Математический анализ
Линейная алгебра
Лекция 5. Матрицы: определения, виды матриц.
Действия над матрицами.
Основные определения
Матрицей называется прямоугольная таблица, состоящая из чисел.
Обозначение матриц: A,B,C,K… - заглавными буквами латинского алфавита.
Горизонтальная линия матрицы – строка, вертикальная – столбец.
Элементы этой
таблицы имеют такое обозначение:
Числа m и n – размер матрицы. Если m=n, то матрица квадратная.
Матрица, все элементы которой – нули, называется нулевой.
Если в квадратной матрице все элементы главной диагонали равны единице, а остальные нулевые, то матрица называется единичной.
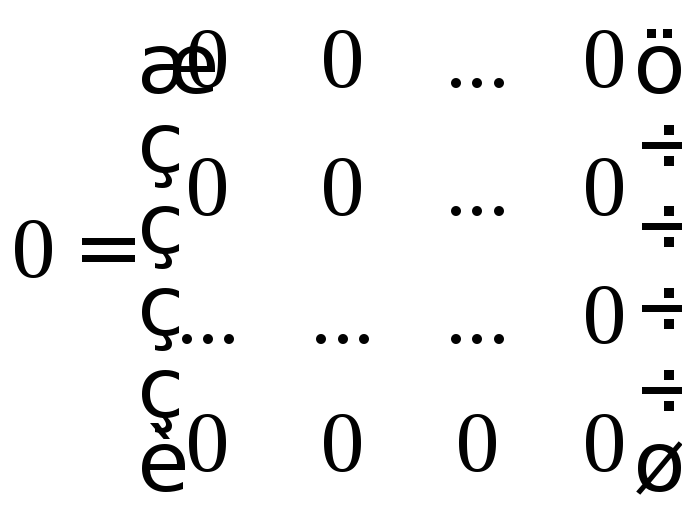

Не следует путать понятие определителя и матрицы. Определитель – одно число, матрица – таблица из чисел. Для любой квадратной матрицы определитель может быть вычислен.
Вектор – это частный случай матрицы, содержащей всего одну строку
Если у матрицы только один столбец, то такая матрица называется вектор-столбцом.
Линейные операции над матрицами
Сложение матриц
Складывать можно только матрицы одинакового размера. Матрицы складываются поэлементно.
![]()
![]()
![]()
Умножение матрицы на число
Любую матрицу можно умножить на число, это делается поэлементно
![]()
Свойства линейных операций над матрицами

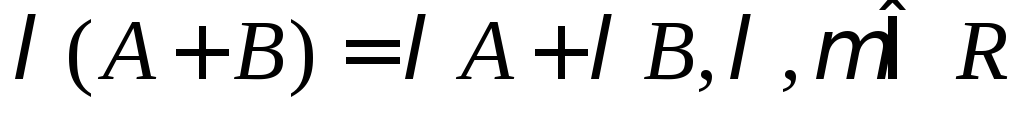

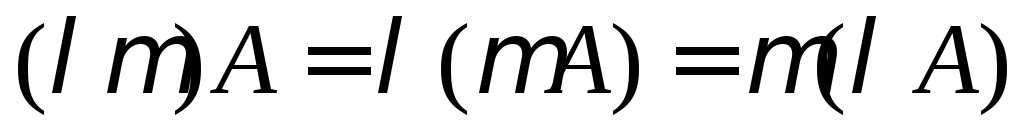

Противоположнаяматрица – матрица, все элементы которой имеют противоположные элементам исходной матрицы знаки.
![]()
![]()
 Это свойство можно
рассмотреть на примере матрицы 2*2
Это свойство можно
рассмотреть на примере матрицы 2*2

Умножение матриц
Пусть матрица Aимеет размерm×n, а матрицаBразмерl×k. Чтобы эти матрицы можно было перемножить, нужно чтобы выполнялось условиеn=l. Тогда произведением будет матрица размераm×k.
Найдем элементы
матрицы произведения
![]() .
Для нахождения каждого элемента
.
Для нахождения каждого элемента
![]() матрицы
С выделимi-ю строчку
матрицыAиj-ю
столбец матрицыB.
матрицы
С выделимi-ю строчку
матрицыAиj-ю
столбец матрицыB.




![]()
Примеры:
Вычисление произведения матриц:
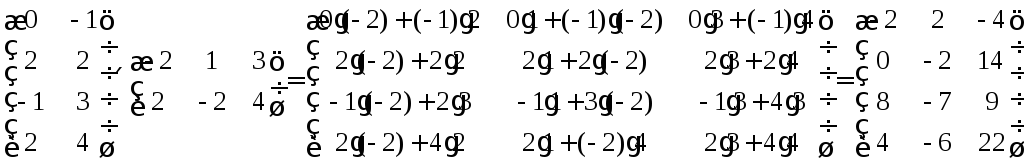
Произведение матрицы на вектор-столбец

Произведение вектор-столбца на вектор-строку


Свойства умножения матриц
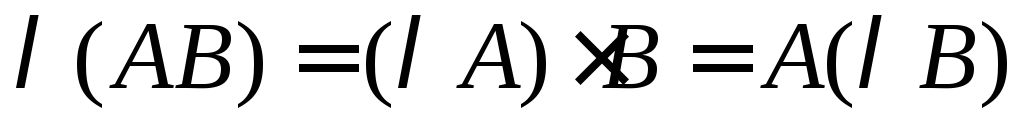


 сочетательный
закон
сочетательный
закон A-квадратная
матрица,E-единичная
A-квадратная
матрица,E-единичная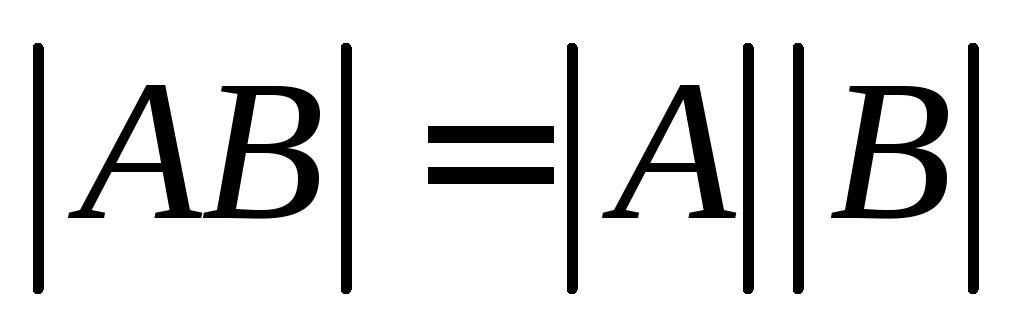 определитель
произведения матриц AиBравен произведению их
определителей.
определитель
произведения матриц AиBравен произведению их
определителей.
Замечание: для квадратных матриц переместительный закон умножения (коммутативность) неверен.
Транспонирование матриц и его свойства
Матрица, у которой строчки заменены столбцами, а столбцы – строчками называется транспонированной по отношению к данной.

Пример:


Свойства транспонирования матриц


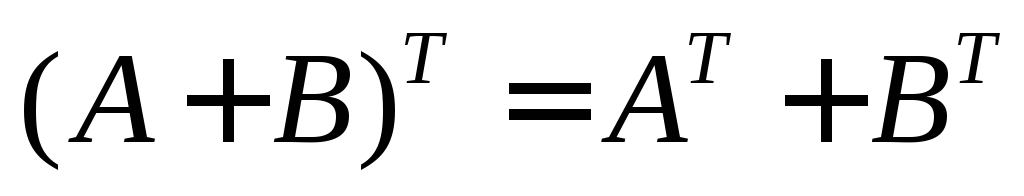

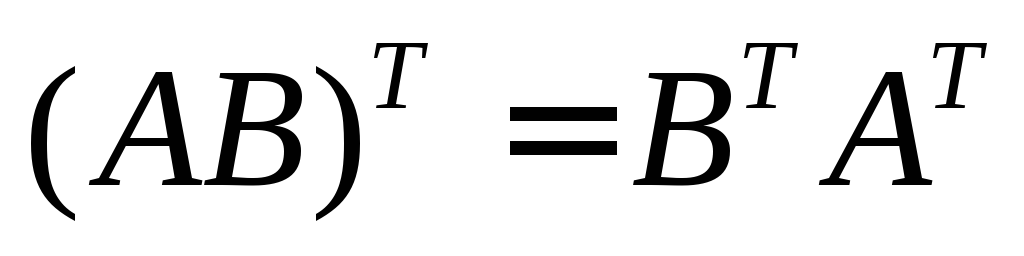
 Определитель
транспонированной матрицы совпадает
с исходным
Определитель
транспонированной матрицы совпадает
с исходным
Обратная матрица и ее вычисление.
Пусть A– квадратная матрица порядкаn,
тогда обратной будем называть (и
обозначать ееA-1)
такую матрицу, что![]() .
.
Обратная матрица определена тогда и только тогда, когда ее определитель отличен от 0.
Обратная матрица вычисляется по следующей схеме:
Пусть задана матрица Bn×n
 ,
тогда
,
тогда

Здесь знаком B* обозначена союзная матрица – транспонированная матрицаалгебраических дополненийисходной матрицы.
Для матрицы второго порядка можно указать простые формулы для нахождения ей обратной.
Пусть дана матрица С размером 2×2. Найдем обратную матрицу:
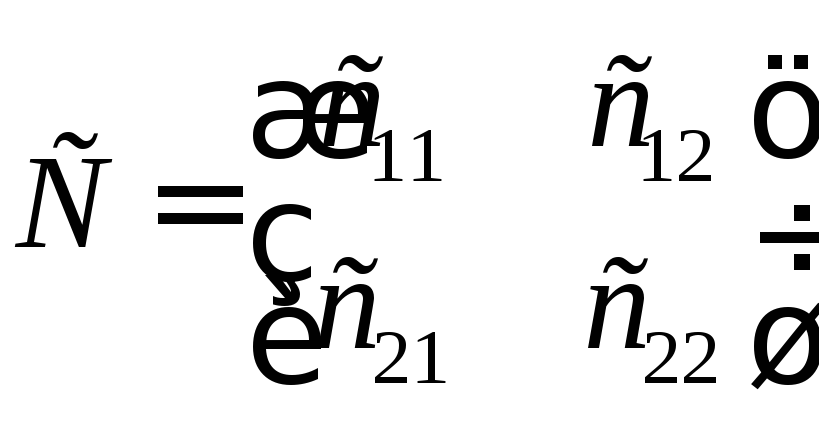
![]()
![]()
![]()
![]()
Союзная матрица:

Перемножим исходную матрицу и союзную:

Отсюда найдем обратную матрицу:
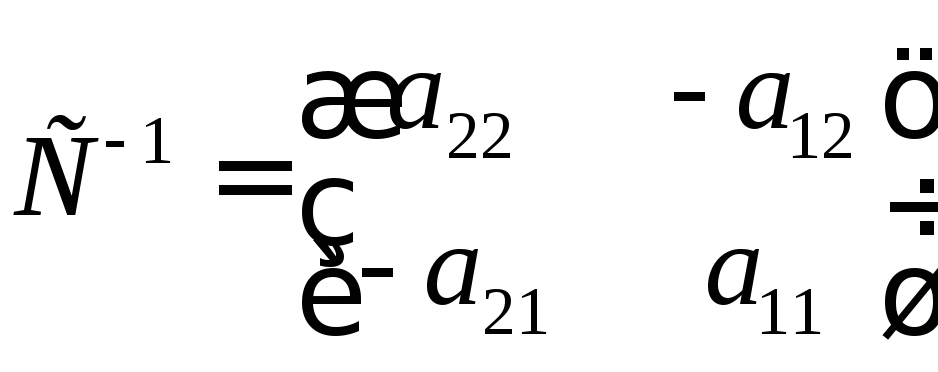 - матрица второго
порядка
- матрица второго
порядка
Пример:
Для матрицы 3×3 найдем ей обратную. Пусть дана матрица:

![]()


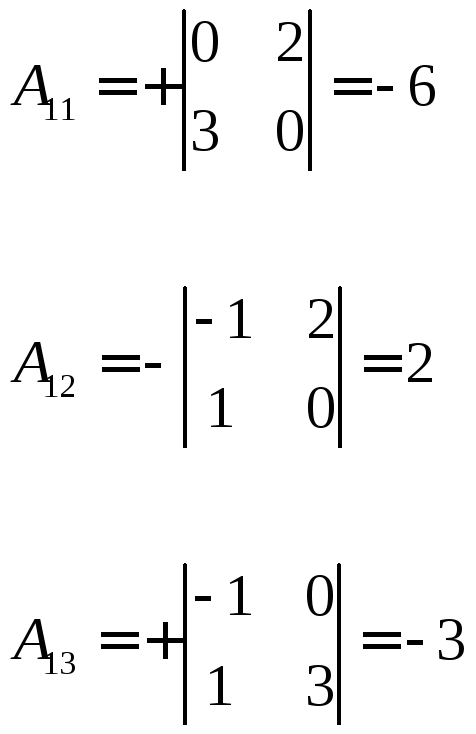

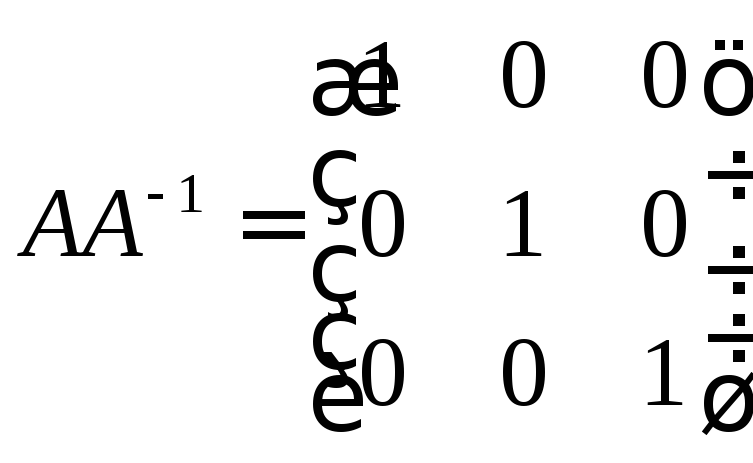
Решение матричных уравнений.
В общем случае
матричное уравнение имеет следующий
вид: либо
![]() ,
тогда его решение находится так:
,
тогда его решение находится так:
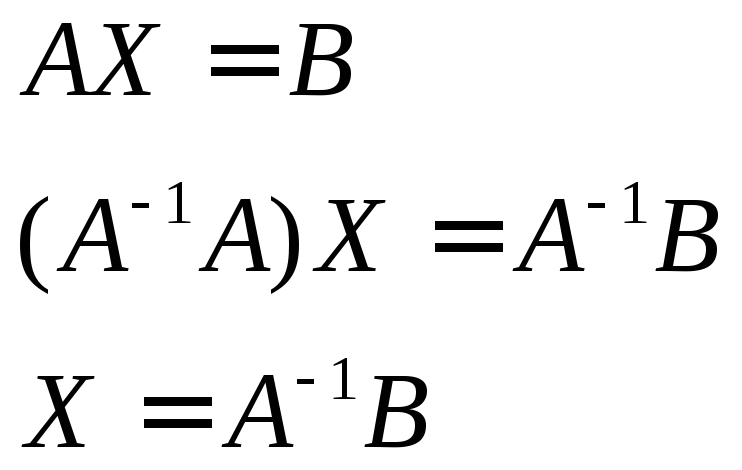
Предполагается,
что X– матрица неизвестных
( ее размер заранее не определен),A– квадратная матрица коэффициентов,
причем![]() ,
матрицаBизвестна из
условия, либо определяется в ходе
алгебраических преобразований более
сложного уравнения.
,
матрицаBизвестна из
условия, либо определяется в ходе
алгебраических преобразований более
сложного уравнения.
Матричное уравнение,
кроме того, моет иметь вид
![]() ,
причем смысл обозначений остается тем
же.Порядок следования
матриц в уравнении важен, так
как уравнение
,
причем смысл обозначений остается тем
же.Порядок следования
матриц в уравнении важен, так
как уравнение ![]() имеет другое решение, чем уравнение
имеет другое решение, чем уравнение![]() ,
а именно:
,
а именно:
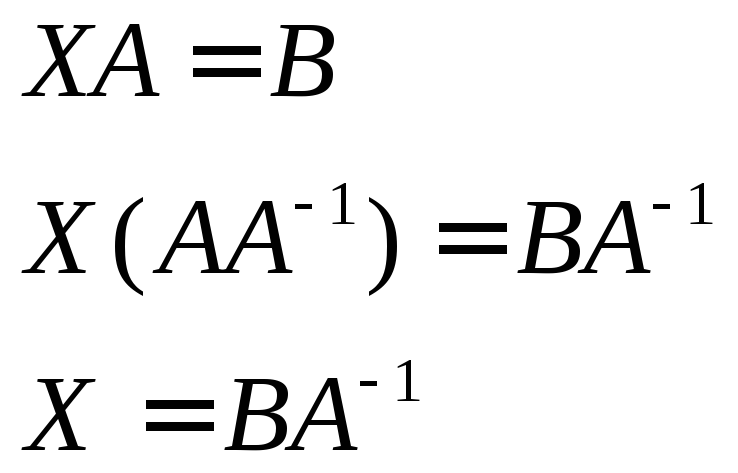
Пример решения матричного уравнения:
![]() .
Здесь
.
Здесь
![]() ,
,![]()
Решение найдем по
формуле
![]()

Проверка:

