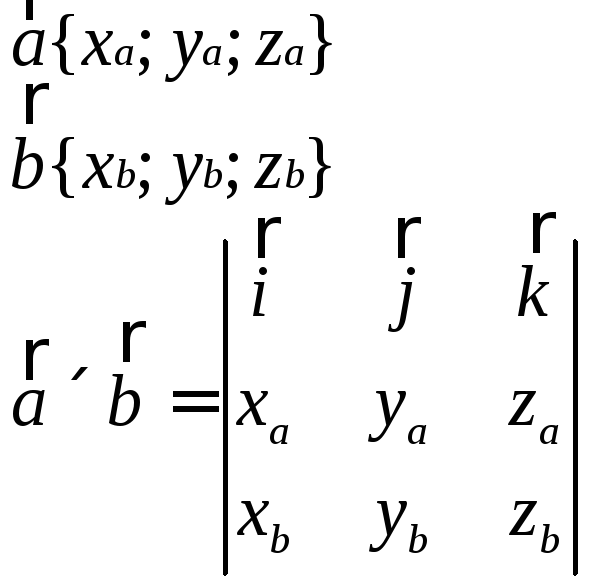- •1 Курс, 1 семестр.
- •Лекция 1. Определители. (рассм. На прк)
- •Свойства определителей (справедливы для определителей любого порядка)
- •Вычисление определителей 4-го и более высоких порядков.
- •Лекция 3. Скалярное, векторное и смешанное произведение векторов и их свойства.
- •Лекция 4. Комплексные числа
- •Линейная алгебра
- •Лекция 5. Матрицы: определения, виды матриц.
- •Действия над матрицами.
- •Основные определения
- •Линейные операции над матрицами
- •Транспонирование матриц и его свойства
- •Лекция 6. Системы линейных алгебраических уравнений и методы их решения (формулы Крамера, матричный метод)
- •Решение систем трех линейных уравнений с тремя неизвестными матричным методом.
- •Лекция 7. Решение систем линейных алгебраических уравнений (слау) методом Гаусса Суть метода Гаусса:
- •Решение однородных слау
- •Лекция 8. Плоскость в пространстве
- •1.1. Общее уравнение плоскости в пространстве
- •1.2. Уравнение плоскости, проходящей через данную точку параллельно двум заданным (неколлинеарным) векторам
- •1.3. Уравнение плоскости, проходящей через три данные точки
- •1.4. Уравнение плоскости «в отрезках»
- •1.5. Нормальное уравнение плоскости
- •1.6. Полярные параметры плоскости
- •1.7. Особые случаи расположения плоскости в пространстве относительно системы координат
- •2. Плоскости в пространстве: взаимное расположение
- •2.5. Угол между плоскостями
- •2.6. Условия параллельности и перпендикулярности плоскостей
- •1.1. Уравнение прямой на плоскости,
- •1.10. Полярные параметры прямой
- •2. Прямые на плоскости: взаимное расположение
- •2.1. Условие, при котором три точки лежат на одной прямой
- •2.2. Взаимное расположение прямой и пары точек
- •2.3. Расстояние от точки до прямой
- •2.4. Пучок прямых
- •2.5. Угол между прямыми
- •2.6. Условия параллельности и перпендикулярности прямых
- •2.7. Точка пересечения непараллельных прямых
- •Лекция 10. Прямая в пространстве
- •Лекция 11. Кривые второго порядка
- •Лекция 12. Поверхности второго порядка
- •Математический анализ
Лекция 3. Скалярное, векторное и смешанное произведение векторов и их свойства.
|
|
Скалярное произведение |
Векторное произведение |
Смешанное произведение |
|
Определение |
Скалярным произведением называется (число) произведение длин векторов на косинус угла между ними
|
Векторным
произведением векторов
|
Смешанным
произведением векторов
|
|
Алгебраические свойства |
|
|
|
|
Геометрические свойства |
|
|
Если
|
|
Физический смысл |
Работа
силы
|
Момент
силы
|
Не определен |
|
Условие ра- венства нулю |
|
|
|
|
Вычисление в декартовой системе координат |
|
|
|
Правило вычисления векторного произведения векторов :
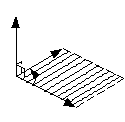
Результирующий вектор имеет направление поступательного движения буравчика при вращении его ручки по направлению от первого вектора ко второму. На рисунке показана левая тройка векторов.
Вывод формул скалярного, векторного и смешанного произведении векторов в декартовой системе координат (ДСК).
Скалярное произведение вектора
 на вектор
на вектор
Найдем скалярное произведение соответствующих ортов:
![]() ,
так как орты – единичные векторы по
определению
,
так как орты – единичные векторы по
определению
![]() ,
так как орты перпендикулярны друг другу.
,
так как орты перпендикулярны друг другу.
С учетом этого
найдем скалярное произведение
![]() на
на
![]() :
:
![]()
Векторное произведение векторов:
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Перемножая вектор
![]() на вектор
на вектор![]() ,
получим:
,
получим:![]()

Смешанное произведение векторов
![]() ,
,
![]() ,
,![]() ,
,
найдем по правилам вычисления векторного и скалярного произведения векторов.

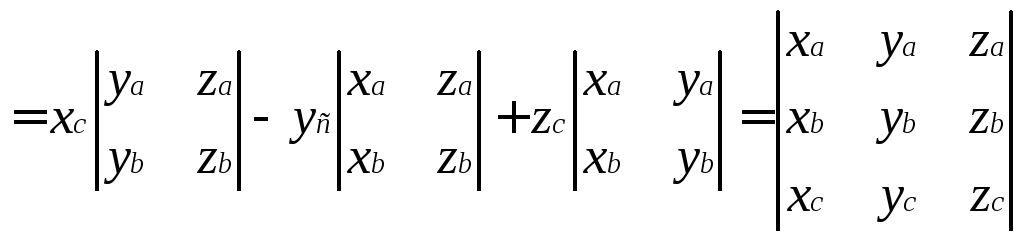
Лекция 4. Комплексные числа
Алгебраическая форма и геометрическая интерпретация комплексных чисел (КЧ).
Под комплексным
числом (КЧ) мы будем понимать абстрактное
выражение
![]() ,
где
,
где![]() ,
а
,
а![]() .
Число
.
Число![]() называют «мнимой единицей». Выражение
вида
называют «мнимой единицей». Выражение
вида![]() -алгебраическая форма
записи комплексного числа.
-алгебраическая форма
записи комплексного числа.

а
– действительная часть
КЧ, b
– мнимая часть
КЧ. Таким образом, если комплексное
число z
представить как ![]() ,
то
,
то![]() ,
а
,
а![]() .
.
Тригонометрическая и показательная форма записи КЧ.
П усть
дано комплексное число
усть
дано комплексное число![]() ,
тогда можно его представить как
,
тогда можно его представить как![]() .
Такой вид записи КЧ называется
тригонометрическим. МножительR
называется модулем КЧ, а число
.
Такой вид записи КЧ называется
тригонометрическим. МножительR
называется модулем КЧ, а число![]() - аргументом. Они определяются из
следующих соотношений:
- аргументом. Они определяются из
следующих соотношений:
![]() ,
,

Обратно к алгебраической форме записи можно перейти по формулам:
 ,
причем
,
причем
![]() ( иногда бывает удобнее использовать
эти формулы наоборот, чтобы записывать
КЧ в тригонометрическом виде).
( иногда бывает удобнее использовать
эти формулы наоборот, чтобы записывать
КЧ в тригонометрическом виде).
В
показательном виде КЧ можно записать
с помощью формулы Эйлера:
![]() ,
тогда
,
тогда![]() .
.
Пример:
записать комплексное число
![]() в тригонометрической и показательной
форме.
в тригонометрической и показательной
форме.
Найдем модуль и аргумент этого КЧ:
![]()
![]()
Окончательно запишем:
![]() .
.
Сложение и умножение комплексных чисел. Их свойства.
Пусть
даны два комплексных числа
![]() и
и![]() .
Найдем их сумму и произведение:
.
Найдем их сумму и произведение:
в алгебраической форме:
![]()
![]()
в тригонометрической и показательной формах записи:
![]()
![]()
Свойства сложения и умножения комплексных чисел:
Свойства сложения:
Свойства умножения:

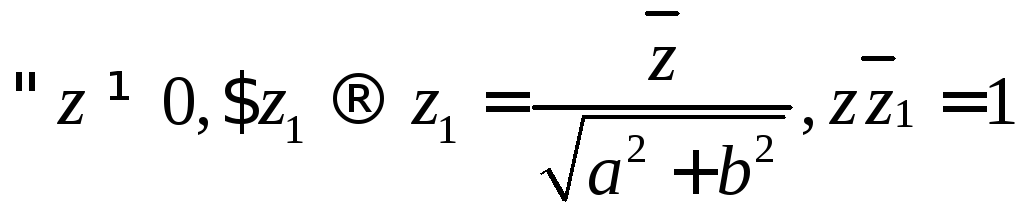 :
для всякого ненулевого комплексного
числа z
существует такое число z1,
равное частному от деления
комплексно-сопряженного числа на модуль
z,
произведение которого на само число
равно 1
:
для всякого ненулевого комплексного
числа z
существует такое число z1,
равное частному от деления
комплексно-сопряженного числа на модуль
z,
произведение которого на само число
равно 1

 - дистрибутивность
умножения КЧ
- дистрибутивность
умножения КЧ
Сопряжение КЧ. Деление КЧ.
Пусть дано
комплексное число
![]() ,
тогда проведя операцию сопряжения
комплексных чисел ( обозначается знаком
,
тогда проведя операцию сопряжения
комплексных чисел ( обозначается знаком![]() )
, получим:
)
, получим:![]() .
В тригонометрической и показательной
форме соответственно имеем:
.
В тригонометрической и показательной
форме соответственно имеем:![]() ,
,![]() .
.
Свойства сопряжения:
![]()
![]()
Деление комплексных чисел
Комплексные
числа можно делить в алгебраической,
тригонометрической и показательной
форме. Пусть имеются два комплексных
числа
![]() и
и![]() .
Частное этих чисел в алгебраическом
виде находится по формуле
.
Частное этих чисел в алгебраическом
виде находится по формуле![]() .
В показательной и тригонометрической
форме частное найдем по формуле
.
В показательной и тригонометрической
форме частное найдем по формуле![]()
Пример:
Разделить
![]() в алгебраической форме.
в алгебраической форме.
![]() .
.
Проверка:
![]()
Формула Муавра. Нахождение корней из комплексных чисел.
Пусть
![]() .
.
Формула Муавра:
![]()
Корни
из комплексного числа – решения уравнения
![]() .
Их существует ровноn
(
.
Их существует ровноn
(![]() ).
Пусть
).
Пусть![]() ,
тогда
,
тогда