3.8. Расчёт червячной передачи. Механизм подъёма пути

электробалластера ЭЛБ-1

Червячные передачи, благодаря своему высокому передаточному отношению и возможности самоторможения, применяются в грузоподъёмных механизмах строительных, путевых и дорожно-строительных машин.

В целях предотвращения усталостного выкрашивания поверхности зуба червячного колеса, червячные передачи рассчитываются на поверхностную выносливость (контактную прочность). Для всех червячных передач, кроме ручных и с числом зубьев колеса более 100, этот расчёт является проектным. Для предотвращения излома зубьев колеса они проверяются на прочность по напряжениям изгиба.

Рассмотрим расчёт червячной передачи на примере редуктора лебёдки механизма подъёма пути электробалластера ЭЛБ-1 [33].

Рис. 3.26. Типовой редуктор лебёдки механизма подъёма пути ЭЛБ-1

Редуктор (рис. 3.26) через муфту передаёт вращение на червячный вал, а червячное колесо имеет в центре трапецеидальную резьбу, толкающую винт, который поднимает приготовленные к укладке пакеты пути.

Электробалластер ЭЛБ-1 имеет несколько таких редукторов для подъёма, сдвига и перекоса пути, которые создают разные усилия (от 6 до 13 тонн) и отличаются размерами червячных передач и подшипников, а также мощностью приводных электродвигателей. Однако их конструкция и принцип действия одинаковы, поэтому они приняты, как типовые [33]. Особенность конструкции наиболее грузоподъёмного редуктора – сборное червячное колесо в виду его значительных размеров ( > 400 мм в диаметре).

Выполним расчёт наиболее грузоподъёмного редуктора, создающего осевое усилие на винте F_вин =13 т (127530 Н).

Для создания такого усилия к винту со стандартной трапецеидальной резьбой d = 40 мм должен быть приложен со стороны ступицы червячного колеса вращающий момент, который приближённо, с учётом угла наклона винтовой линии резьбы [34], можно оценить, как

M₂ ≈ 0,18· F_вин·d = 0,18·127530·40 = 918216 ≈ 920000 Нмм.

Силовая передача потребует электродвигатель с небольшой частотой вращения n₁ = 750 об/мин. Передаточное отношение примем стандартное U = 20. Частота вращения червячного колеса n₂ = n₁/U = 750/20 = 37,5 об/мин. Угловые скорости вращения валов ω₁ = 78,5 с⁻¹, ω₂ = 3,93 с⁻¹.

Мощность, которая должна дойти до червячного колеса

N₂ = M₂·ω₂ = 920000·10⁻³ ·3,93 = 3616 Вт.

КПД червячного редуктора можно предварительно оценить [18], как

η ≈ 0,9(1−U/200) ≈ 0,81.

Тогда требуемая мощность электродвигателя

N₂ = N₂/η = 3616/0,81 = 4463 Вт ≈ 4,5 кВт.

Таким параметрам соответствует асинхронный двигатель (табл. 2.1, 2.2) 4А132М8У3, который, с учётом его КПД η_эдв = 82% при паспортной мощности N_эдв =5,5 кВт, обеспечит для редуктора требуемую мощность на валу червяка N₂ = N_эдв/η_эдв = 5,5/0,82 = 4,51 кВт с частотой вращения 750 об/мин.

Расчётный срок службы редуктора Т = 40000 часов.

По этим исходным данным выполняем расчёт червячной передачи [48].

Выбираем материалы деталей по табл. 3.1:

– для червяка сталь 18ХГТ с цементацией на НRС56…62; E₁ = 2,1·10⁵ Н/мм²; коэффициент Пуассона μ₁ = 0,3;

– для колеса бронзу БрО10Ф1 E₂ = 1,01·10⁵ Н/мм²; μ₂ = 0,3; предельное контактное напряжение σ_Hlim2 = 234 Н/мм²; предельное изгибное напряжение σ_Flim2 = 58 Н/мм².

Базовые числа циклов нагружения:

для контактных напряжений N₀=10⁷; для изгибных напряжений N₀=10⁶.

Фактическое число циклов нагружения зуба колеса

N_E = T·n₂·60 = T·n₁·60/u =4·10⁴·750·60/20 = 0,9·10⁸ ≈ 10⁸ циклов.

Если окажется, что N_E > 2,5·10⁸, то принимают N_E = 2,5·10⁸;

Если N_E < N₀, то принимают N_Е = N₀ и тогда в качестве допускаемых принимаются предельные напряжения σ_Hlim, σ_Flim.

В этих двух случаях необходимо будет пересчитать срок службы механизма T_факт = N_E· U /n₁ · 60.

Рассчитываем допускаемые напряжения с учетом фактических условий нагружения.

Допускаемые контактные напряжения материала колеса:

Допускаемое напряжение изгиба:

Определяем число заходов червяка из условия Z₁ > Z_2min / U. Для несиловых передач Z_2min = 17, для силовых Z_2min= 26. Таким образом, Z₁ > 26/20 > 1,3. Примем Z₁ = 2. Считаем число зубьев колеса Z₂ = Z₁·U = 2·20 = 40.

Выбираем коэффициент диаметра червяка, q в соответствии с рекомендациями ГОСТ 2144-93 по оптимальному сочетанию с модулем m (табл. 3.14).

Выбираем коэффициент диаметра червяка q = 8, сочетающийся с любыми модулями.

Вычисляем приведённый модуль упругости материалов червяка и колеса

Находим коэффициент деформации червяка (табл. 3.15) для двухзаходного червяка с коэффициентом диаметра q = 8 найдём Θ = 57.

Коэффициент концентрации нагрузки K_β = 1+(Z₂/Θ)³ =1+(40/57)³=1,346.

Скоростной коэффициент K_V = 1…1,3. Выбираем среднее K_V = 1,15.

Коэффициент нагрузки K = K_β · K_V = 1,346 · 1,15 = 1,55.

Таблица 3.14 Сочетание модулей m и коэффициентов диаметра q червяка (+ рекомендуемое, − недопустимое)

Коэффициент диаметра червяка q по ГОСТ 19672-74

6,3

(7,1)

(7,5)

8,0

(9,0)

10

(11,2)

(12)

12,5

(14)

16

(18)

20

(22,4)

25

Модуль m по ГОСТ 2144-76

1 ; 1,25

−

−

−

−

−

−

+

+

+

+

1,6

−

−

−

−

−

+

+

+

+

+

2

−

−

−

+

+

+

+

+

+

2,5

−

−

−

+

+

+

+

+

+

(3)

−

−

−

+

+

+

3,15

−

−

−

+

+

+

+

+

+

(3,5)

−

−

−

+

+*

+*

4

−

+

+

+*

+

+

+

+

5

+

+

+

+

+

+

+

+

(6)

+

+

6,3

+

+

+

+

+

+

+

+

+

+

(7)

+

8

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

10

+

+

+

+

+

+

+

+

+

+

+

+

+

+

−

(12)

+

+**

−

−

12,5

+

+

+

+

+

+

+

+

+

−

−

(14)

+***

−

−

−

16

+

+

+

+

+

+

+

−

−

−

−

20

+

+

+

+

+

−

−

−

−

−

−

−

Примечание. В скобках даны дополнительные значения модуля и коэффициента диаметра.* – только при Z1 = 1; ** – только при Z1 = 1 и 2; *** – только при Z1 = 2.

=‒

Таблица 3.15 Коэффициент деформации червяка Θ
Число заходов, Z1	Коэффициент диаметра червяка q по ГОСТ 19672-74
	6,3	(7,1)	(7,5)	8,0	(9,0)	10	(11,2)	(12)	12,5	(14)	16	(18)	20	(22,4)	25
1	44	57	66	72	89	108	127	143	157	176	225	280	318	373	434
2	35	45	52	57	71	86	102	117	125	152	185	233	259	304	353
3	30	40	47	51	61	76	89	105	110	134	162	202	215	263	307
4	28	37	43	47	58	70	82	98	101	123	148	186	206	243	280
Примечание. В скобках даны дополнительные значения коэффициента диаметра.

Угол подъёма винтовой линии червяка γ = arctg(Z1/q) = arctg(2/8) = 14°1'48".

Угол зацепления α = 20°. Осевой модуль зацепления

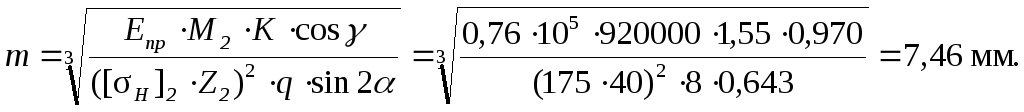
Принимаем из нормального ряда ближайший больший модуль m = 8.

Эквивалентное число зубьев Z_V = Z₂ / cos³ γ = 40/cos³14°1'48" = 43,8.

Коэффициент прочности зуба (табл. 3.16) для эквивалентного числа зубьев 43,8 Y_H = 1,50.

Проверяем прочность червячного колеса по напряжениям изгиба

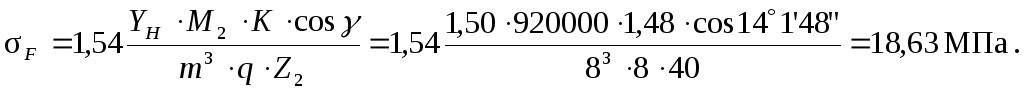
Таблица 3.16 Коэффициенты прочности зубьев червячных колес YH при различных эквивалентных числах зубьев ZV
ZV YH	ZV YH	ZV YH	ZV YH
20 1,98	30 1,76	40 1,55	80 1,34
24 1,88	32 1,71	45 1,48	100 1,30
25 1,85	35 1,64	50 1,45	150 1,27
28 1,80	37 1,61	60 1,40	300 1,24

Условие прочности на изгиб выполняется, т.к. напряжения меньше допускаемых (42,53 МПа).

Рассчитываем геометрические параметры передачи:

– межосевое расстояние A_W = m·((Z₂ + q)/2) = 8·((40+8)/2) = 192 мм;

– размеры червяка:

диаметр делительного цилиндра d_W1 = m · q = 8·8 = 64 мм;

диаметр цилиндра вершин d_a1 = d_W1 +2m = 64 + 2·8 = 80 мм;

диаметр цилиндра впадин d_f1 = d_W1 −2,4m = 64 − 2,4·8 = 44,8 мм;

длина нарезанной части червяка b₁ = (C₁+C₂·Z₂)m

при Z₁ = 1,2 C₁ = 11; C₂= 0,06;

при Z₁ = 4 C₁ =12,5; C₂ = 0,09;

тогда b₁ = (11 + 0,06·40)·8 = 107,2 мм;

– размеры червячного колеса:

диаметр делительной (начальной) окружности в среднем сечении

d_W2 = m · Z₂ = 8 · 40 = 320 мм;

диаметр окружности впадин в среднем сечении

d_f2 = d_W2 − 2,4m = 320 − 2,4·8 = 300,8 мм;

диаметр окружности вершин в среднем сечении

d_a2 = d_W2 +2m = 320 + 2·8 = 336 мм;

наибольший диаметр колеса

d_am2 = d_a2 + 6m / (Z₁ +2) = 336 + 6·8/(2+2) = 348 мм;

ширина зубчатого венца червячного колеса b₂ = A · d_a1 для Z₁ = 1 и 2 принимаем A = 0,75; при Z₁ = 4 A =0,67; тогда b₂ = 0,75 · 96 = 72 мм;

условный угол обхвата

2δ = 2arcsin[b₂/(d_a1−0,5m)] = 2arcsin[72/(96−0,5·8)] = 110°51'51".

Рассчитываем силы, действующие в зацеплении:

− окружная сила на колесе, равная осевой силе на червяке

F_t2 = F_a1 = 2M₂ / d_W2 = 2 · 900000/320 = 5625 H;

− окружная сила на червяке, равная осевой силе на колесе

F_t1 = F_a2 = 2M₁/d_W1 = 2·57300/64 = 1790 H;

− радиальная сила: F_r1 = F_r2 = F_t2· tgα = 5625·tg20° = 2050 H.

Рассчитываем скорость скольжения

V_cк = πd_W1n₁/(60·1000·cosγ) = 3,14·64·750/(60000·cos14°1'48") = 2,58 м/с.

Коэффициенты и углы трения для рассчитанной скорости скольжения:

Таблица 3.17 Коэффициенты трения ƒ и углы трения φ = arctg ƒ для стального червяка и колеса из бронз и чугунов

Vск, м/с

0,01

0,1

0,25

0,5

1

1,5

2

2,5

3

4

7

10

15

ƒ

0,10 … 0,12

0,08 … 0,09

0,065… 0,075

0,055… 0,065

0,045… 0,055

0,04 … 0,05

0,035… 0,045

0,03 … 0,04

0,028… 0,035

0,023… 0,03

0,018… 0,026

0,016… 0,024

0,014… 0,020

φ

5°40' … 6°50'

4°30' … 5°10'

3°40' … 4°20'

3°10' … 3°40'

2°30' … 3°10'

2°20' … 2°50'

2°00' … 2°30'

1°40' … 2°20'

1°30' … 2°00'

1°20' … 1°40'

1°00' … 1°30'

0°55' … 1°20'

0°50' ... 1°10'

Примечание. Меньшие значения φ относятся к венцам из оловянных бронз, большие – к безоловянным бронзам, латуни и чугунам.

для V_cк = 2,58 м/с и оловянной бронзы БрО10Ф1: φ =1°40'; ƒ = 0,03.

Коэффициент полезного действия червячной передачи

η = tg γ / tg(γ + φ) = tg14°1'48" / tg(14°1'48"+1°40') = 0,8989 ≈ 89 % .

По полученным геометрическим параметрам червяка и колеса выполняются рабочие чертежи (рис. 3.27, 3.28).