Кол. методы МБА 2012 / 1. Статистика / Книга по стат. методам / Книга

•Как, например, используя имеющуюся статистику, оценить шансы того, что изучаемый показатель будет находиться в некотором конкретном диапазоне значений, или не превысит некоторого критического уровня?

2.2. Группировка данных. Ряд распределения

Одним из эффективных методов обработки одномерных массивов является группировка данных – разбиение всего диапазона изменения показателя на группы (интервалы) с подсчетом числа наблюдений (частот), попавших в ту или иную группу или их доли (относительных частот). Это позволяет оценить, в каких интервалах значений исследуемая величина появляется чаще, а в каких реже. Подобный подход с одной стороны приводит к потере части информации, а с другой позволяет превратить неупорядоченный набор выборочных данных, в картину, показывающую, насколько часто значения исследуемой величины появляются в том или ином диапазоне ее изменения. Основные идеи метода группировки иллюстрирует следующий пример.

Пример. 2.1. Количество посетителей кафе в период бизнес ленча колеблется от 16 до 25 человек в час. Для своевременного обслуживания посетителей владельцу кафе необходимо обеспечить в этот период соответствующее количество обслуживающего персонала и необходимый запас продуктов. Информация (статистика) о числе посетителей кафе за последние 50 дней приведена в таблице 2.2.

Таблица 2.2.

Количество посетителей кафе в период бизнес ленча

21

Вопросы

1.На какое количество посетителей целесообразно ориентироваться, чтобы правильно определить запас необходимых блюд и назначить оптимальное число сотрудников, обслуживающих клиентов?

2.Как оценить шансы того, что число посетителей не превысит, например, 28 человек?

Решение

1. Упорядочим исходные данные по возрастанию (проранжи-

руем ряд): 16, 17, 18, 18, 19, 19, 20, 20, 20, 21, 21, 21, 21, 22, 22, 22, 22, 22, 23, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25, 26, 26, 27, 27, 28, 28, 28, 29, 29, 29, 30, 32.

Как видно, наименьшее число посетителей кафе по данным имеющейся выборки составило Ymin = 16 человек, а максимальное Ymax = 32 человека.

2.Разобьем диапазон от 16 до 32 посетителей на 9 интервалов одинаковой «длины» [14-16], [16-18], [18-20], [20-22], …, [28-30], [30-32].

3.Подсчитаем количество наблюдений, попадающих в каждый из интервалов. При этом полагаем, что если число посетителей в точности совпадет с правой границей интервала, то оно считается принадлежащим данному интервалу. Анализируя ранжированный ряд, устанавливаем, что в интервал до 16 посетителей попадает одно наблюдение (16), в интервал от 16 до 18 – три наблюдения (17, 18, 18), в интервал [18-20] – пять наблюдений (19, 19, 20, 20, 20) и т.д.

Результаты подсчетов занесем в таблицу 2.3 (столбец «Частота»).

4.Для оценки доли числа посетителей, находящихся в том или ином диапазоне значений, вычислим относительные частоты.

Заметим, что с содержательной точки зрения каждый интервал определяет конкретное событие, например, интервал [26-28] соответствует событию «кафе посетят от 26 до 28 человек». Следовательно, относительная частота является не чем иным, как оценкой частоты такого события.

Так, относительная частота события «число посетителей не превысит 16 человек» равна, по данным выборки, состоящей из 50 наблюдений:

P1 (число посетителей будет не более16) = 501 100% = 2% .

22

Аналогично частота события «число посетителей составит от 16 до 18» человек:

P2 (число посетителей будет от16 до18) = 503 100% = 6% .

5. Вычисляя относительные частоты для остальных интервалов, заносим их в таблицу 2.3 (столбец «Относительная частота»).

Таблица 2.3.

6. Используя данные последнего столбца таблицы 2.3, строим гистограмму ряда распределения (рис. 2.1), дающую возможность наглядно оценить характер и особенности посещаемости кафе в период бизнес ленча.

Рис. 2.1.

23

Чаще всего (в 24% случаев) кафе посещают от 22 до 24 человек. Если рассмотреть более широкий диапазон – от 20 до 26 человек, то таковой численность посетителей бывает, по данным выборки, в 62% случаев (18% + 24% + 20%). А шансы того, что число посетителей не превысит 28 человек, можно оценить (рис. 2.1) как

100% – 10% (8% + 2%) = 90%.

Формальный алгоритм группировки данных для построения ряда распределения заключается в следующем.

1.Находят минимальное Ymin и максимальное Ymax значения среди выборочных данных, представленных в табл. 2.1.

2.Весь диапазон изменения величины Y от Ymin до Ymax разби-

вают на интервалы (карманы) одинаковой «длины» – рис. 2.2. Количество интервалов (k) и их «длину» определяют исходя из содержательного смысла анализируемого показателя и задач исследования. На практике число интервалов выбирают не менее 5 и не более 15.

Рис. 2.2.

3. Подсчитывают, сколько наблюдений попало в каждый из таких интервалов (частоты)

n1, n2 , K, ni , L, nk .

4. Наряду с подсчетом числа наблюдений, попавших в тот или иной интервал (частот), вычисляют относительные частоты – доли наблюдений, оказавшихся в том или ином интервале. Для целей последующего анализа их, как правило, удобнее вычислять в процентах

P1 = nN1 100%,…, Pi = nNi 100% , …, Pk = nNk 100% ,

где ni – число наблюдений, попавших в i-й интервал [Y(i−1) , Y(i ) ], N – число наблюдений (объем выборки).

24

5. Результаты вычислений фиксируют в таблице (табл. 2.4).

6. Используя, в зависимости от целей анализа, второй или третий столбец строят график – гистограмму, характеризующую особенности распределения исследуемого показателя в зависимости от его значений.

2.3.Построение рядов распределения

игистограмм в Excel

Обработка реальных выборочных данных с построением рядов распределения и гистограмм «вручную» может оказаться весьма трудоемкой задачей. Для этих целей можно использовать стандартное программное обеспечение современных ПК и, в частности, инструменты MS Excel.

Наряду с хорошо известными возможностями Excel по проведению расчетов с помощью библиотеки встроенных стандартных функций – математических, статистических, финансовых и других, дополнительные возможности для моделирования представляют так называемые надстройки.

Надстройки – это особые приложения, позволяющие расширить стандартные возможности Excel. Они созданы в виде самостоятельных программных модулей. Информация, введенная в электронную таблицу, переносится в соответствующий программный модуль, обрабатывается там и затем возвращается на рабочий лист

25

в виде результатов. Любую надстройку при необходимости можно активировать и после проведения вычислений, «выгрузить» из памяти.

Для статистического моделирования и анализа статистических данных в Excel предназначена надстройка «Пакет анализа» – набор программ для обработки статистических данных и прогнозирования. «Пакет анализа» не появляется в меню Excel автоматически при уста-

новке Microsoft Office или Excel

на компьютер.

Для активации надстроек в

Excel версии 2003-2007, необхо-

димо в пункте меню «Сервис» выбрать раздел «Надстройки» и в открывшемся диалоговом окне (рис. 2.3) поставить флажок в окошке «Пакет анализа». После чего в пункте меню «Сервис» появится строка «Анализ данных...» (рис. 2.4). В дальнейшем вызов надстройки выполняется из пункта меню Сервис ¾ Анализ данных ....

Рис. 2.4.

26

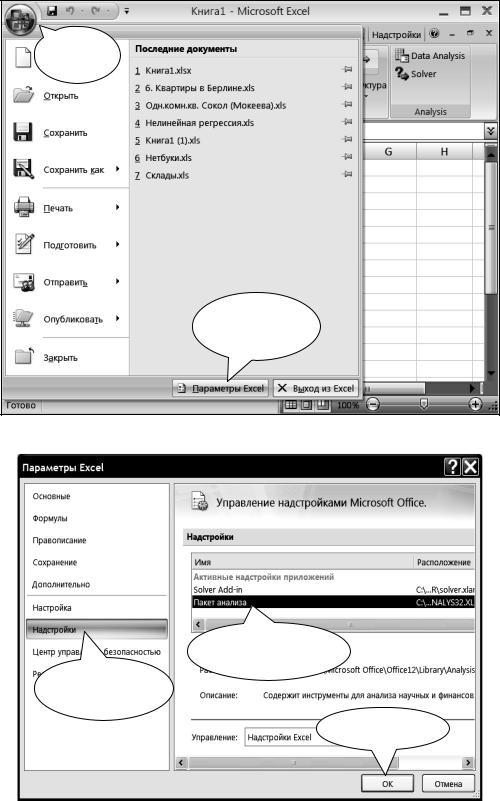
В Excel-2007 для активации надстройки «Пакет анализа» необходимо нажать кнопку «Офис» ¾ войти в «Параметры Excel» ¾

вокне «Параметры Excel» выбрать «Надстройки» ¾ активировать

вправой части окна надпись «Пакет анализа» ¾ нажать кнопку

«ОК» – рис. 2.5, 2.6.

Кнопка

“Office”

Войти в «Параметры

Excel»

Рис. 2.5.

Выделить «Пакет анализа»

Войти в «Надстройки»

Нажать «ОК»

Рис. 2.6.

27

После этого в пункт меню «Данные» добавится раздел «Ана-

лиз данных» («Data Analysis») – рис. 2.7.

Пункт

меню «Анализ «Данные» данных»

Рис. 2.7.

Вдальнейшем вызов надстройки выполняется из пункта меню

«Данные» ¾ Анализ данных ....

Вдиалоговом окне «Анализ данных» – рис. 2.8. Excel приведены девятнадцать различных инструментов для обработки статистики.

Рис. 2.8. Диалоговое окно «Анализ данных».

Для группировки данных, построения ряда распределения и гистограмм предназначен инструмент «Гистограмма». После вы-

28

зова инструмента «Гистограмма» появляется диалоговое окно – рис. 2.9.

Рис. 2.9. Диалоговое окно инструмента «Гистограмма».

Окно «Входной интервал» «Гистограммы» (рис. 2.6.) предназначено для ввода адресов ячеек, в которых расположены данные выборки (предварительно выборочные данные необходимо записать либо в один столбец, либо в одну строку).

Если строка или столбец выборочных данных содержит текстовой заголовок, то в окне надписи «Метки» необходимо установить флажок.

По терминологии, принятой в Excel, интервалы, на которые разбивается диапазон изменения исследуемого показателя, называются «карманами». Окно «Интервал карманов» предназначено для ввода адресов тех ячеек, в которых указаны границы интервалов. Для этого на рабочем листе Excel необходимо предусмотреть соответствующие ячейки, куда заблаговременно следует ввести значения границ интервалов (карманов)

Ymin , Y(1) , Y(2) , …, Y(i−1) , Y(i ) , …, Y(k −1) , Ymax .

Разбиение диапазона изменения показателя от Ymin до Ymax , а именно – определение числа разбиений (числа интервалов), шири-

29

ны каждого интервала и значений границ, целесообразно выполнять вручную.

Для нахождения максимального и минимального значений выборочных данных можно использовать стандартные функции

Excel – пункт меню Вставка ¾ Функция ¾ Категория «Статистические» ¾ МАКС (…), МИН(…).

Если в окне «Интервал карманов» не указывать адреса ячеек с границами, то Excel самостоятельно разобьет диапазон Ymin – Ymax

на карманы и подсчитает число выборочных данных, оказавшихся в каждом из них. Однако делать это не рекомендуется, так как чаще всего такое автоматическое разбиение не всегда соответствует задачам реального анализа. Кроме того, границы интервалов при автоматическом разбиении могут оказаться не целыми числами, что не всегда соответствует реальным выборочным данным, отражающим, например, число покупателей, количество проданных единиц техники и т.д.

Вывести результаты подсчета частот – количества данных из выборки, попавших в тот или иной «карман» (интервал), можно тремя способами.

–На тот же рабочий лист, на котором размещены исходные данные. Для этого в окне «Выходной интервал» указывают адрес ячейки для левого верхнего «угла» выводимой таблицы с результатами расчетов;

–На новый рабочий лист. В этом случае в окне «Новый рабочий лист» указывают имя листа из той же рабочей книги-файла, в которой производятся вычисления.

–В новую рабочую книгу. Для этого в окне «Новая рабочая книга» необходимо указать ее адрес.

Для графического представления ряда распределения «Гистограмма» «предлагает» три вида графиков.

Для получения «классической» гистограммы, аналогичной той, которая изображена на рис. 2.1, следует установить флажок у надписи «Вывод графика».

Частотное распределение можно также представить в виде отсортированной гистограммы Парето. В этом случае столбцы гистограммы будут расположены в порядке убывания по «высоте» слева –

Найти минимальное и максимальное значение можно также с помощью «Пакета анализа», используя инструмент «Описательная статистика»: пункт меню Сервис ¾ Анализ данных ... ¾ Описательная статистика – подробнее см. п.п.3.2.

30