Книга

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(ln x−ln a)2

.pdf

Скачиваний:

114

Добавлен:

08.04.2015

Размер:

3.32 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 3122 23 24 25 26 27 28 29 30 31 > Следующая >>>

В математической статистике и теории вероятностей установ-

лено, что сумма независимых случайных величин, каждая из кото-

рых может иметь любой закон распределения, распределена по нормальному закону. Причем, чем больше число слагаемых, тем ближе к нормальному закону распределена их сумма. Кроме того, он является предельным законом, к которому приближаются другие законы распределения при выполнении определенных условий. В экономике, где на экономический результат оказывает влияние огромное число самых разнообразных факторов, этот закон играет исключительно важную роль.

Нормальный закон распределения характеризуется функцией плотности вероятности вида

f (x) =		1	e−	( x−μ)2
f (x) =	σ	1	e−	2σ 2			(П1.4)
	σ	2π
Как следует из (П1.4) он полностью определяется двумя па-
раметрами – μ и σ , где μ – математическое ожидание, σ – стан-
дартное отклонение.
Кривая функции плотности вероятности случайной величины,
распределенной по нормальному закону, показана на рис. П1.11.
f(x)					1	−	( x −μ)2
					1	−	2σ2
			f (x) =		σ 2π	e
							X
3σ		μ			3σ
Рис. П1.11.
							211

Для среднеквадратического отклонения нормально распреде-
ленной случайной величины получен ряд важных для практики ре-
зультатов. В частности
	P( μ −3σ < X < μ + 3σ ) = 0,9973
Этот результат – правило трех сигм означает, что с вероят-
ностью практически равной единице можно утверждать, что слу-
чайная величина X, распределенная по нормальному закону, за-
ключена	в интервале μ ± 3σ . Или, в	другой формулировке –
практически все значения случайной величины, распределенной по
нормальному закону, лежат в диапазоне μ ± 3σ .
Чем больше значение σ, тем шире диапазон изменения нор-
мально распределенной случайной величины (рис. П1.12).
	Нормальное распределение при одинаковом
0,1	математическом ожидании и разных стандартных
	отклонениях σ1 > σ2
0,08
0,06		σ2

0,04
0,02		σ1
	μ

0
	3σ2	3σ2
	Рис. П1.12.
Вероятности того, что нормально распределенная случайная
величина лежит в других диапазонах, «кратных» стандартному от-
клонению, определяется формулами

P(μ − 2σ < X < μ + 2σ ) = 0,9545

P(μ −σ < X < μ +σ ) = 0,6827

212

Для практических целей удобно использовать, в частности, тот факт, что 90% значений случайной величины заключены в интервале μ ± (1,64)σ :

P( μ −1,64σ < X < μ +1,64σ ) ≈ 0,9 ,

а95% значений случайной величины заключено в интервале

μ± (1,96)σ

P(μ −1,96σ < X < μ +1,96σ ) ≈ 0,95

Зная μ, σ нормального закона распределения, всегда можно

найти (оценить) доверительные интервалы для интересующих аналитика значений и диапазонов случайной величины.

Вероятность того, что случайная величина заключена в произвольном интервале (a,b)

( x−μ)2

( x−

P(a < x <b) = ∫b

∫b e−

f (x) dx =

2 σ 2

dx ≈

2 S 2

σ 2π

S 2π

Для вычисления этого интеграла и решения ряда других задач созданы специальные таблицы, а в Excel предусмотрена стандартная функция НОРМРАСП (…) – пункт меню Вставка ¾ Функция ¾ Категория «Статистические» ¾ НОРМРАСП (… ) –

рис. П1.13, П1.14.

Рис. П1.13.

213

Рис. П1.14.

Если для нормально распределенной случайной величины известны значения μ, σ или их оценки, вычисленные на основе имею-

щейся статистики – X , S (в этом случае полагают μ ≈ X , σ ≈ S ), то

с помощью стандартных функций Excel можно вычислить вероятности того, что случайная величина окажется в том или ином диапазоне значений.

Для вычисления в Excel нужной вероятности в какой либо из ячеек рабочего листа Excel необходимо записать правые части одной из следующих формул:

y Вероятность того, что значения случайной величины X примут значения, меньшие, чем a (рис. П1.15):

P ( X < a) = НОРМРАСП ( a; μ; σ; ИСТИНА)

f(x)

P (X < a)

Рис. П1.15.

214

y	Вероятность того, что значения	случайной	величины	X
примут значения, большие, чем b (рис. П1.16):
	P ( X > b ) = 1 – НОРМРАСП ( b; μ; σ; ИСТИНА).
	f(x)	P (X > b)
	b	x
	Рис. П1.16.
y Вероятность того, что значения случайной величины X бу-
дут находиться в диапазоне от a до b (рис. П1.17):

P ( a < X < b) = НОРМРАСП ( b; μ; σ; ИСТИНА) –

– НОРМРАСП ( a; μ; σ; ИСТИНА)

f(x)	P(a < X < b)
	P(a < X < b)
a	b	x
	Рис. П1.17.

Во многих задачах практики весьма актуальной бывает «обратная» задача (рис. П1.18).

215

f(x)
P(X < b) = Pзад.
b = ?	x
Рис. П1.18.
А именно: требуется найти такое граничное (критическое)
значение b, которое с заданной вероятностью Pзад. = γ	не будет пре-
вышено. Критическое значение b называют квантилем уровня γ .
Для решения такой задачи в Excel предусмотрена специальная
функция НОРМОБР(…) . Вызов функции: Вставка ¾ Функция ¾
Категория «Статистические» ¾ НОРМОБР(…) – рис. П1.19,
П1.20.

Рис. П1.19.

216

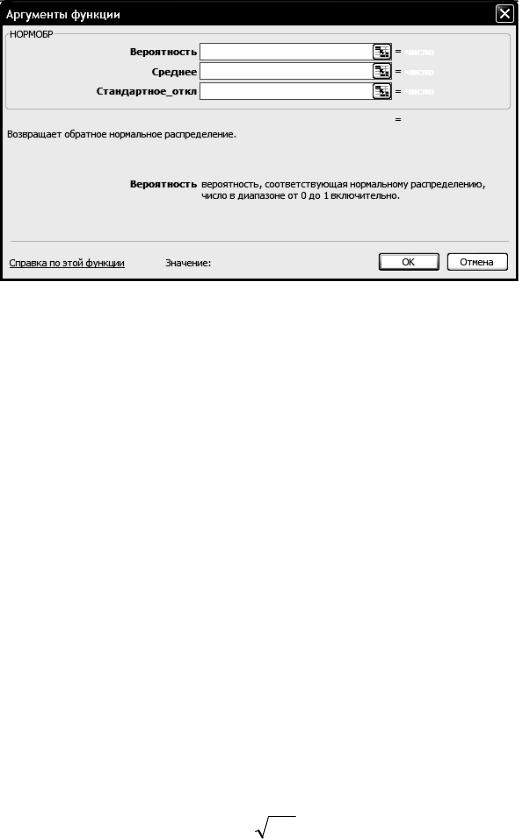
Рис. П1.20.

Для нахождения такого критического значения b в Exel в одной из ячеек рабочего листа необходимо записать правую часть формулы b = НОРМОБР ( Pзад.; μ; σ )

П1.3.5. Логарифмически нормальное распределение

В ряде экономических задач, связанных с изучением распределения доходов, заработных плат, сроков эксплуатации, долговечности устройств и некоторых других, встречаются распределения, получившее название логарифмически нормальных.

Непрерывная случайная величина X имеет логарифмически нормальное распределение, если ее натуральный логарифм ln(X ) подчинен нормальному закону распределения ln(X ) ~ N(a; σ) .

Функция плотности вероятности случайной величины X, имеющей логарифмически нормально распределение имеет вид

Числовые характеристики распределения:

yМатематическое ожидание μx = a eσ 2 2 .

yДисперсия σx2 = a2 eσ2 (eσ2 −1) .

217

График функции плотности вероятности логарифмически нормального распределения показан на рис. П1.21.

f(x)

μ =1; σ =1

μ =2; σ =0,5

μ =2,5; σ =0,45

Рис. П1.21.

Для проведения расчетов и оценок случайных величин, распределенных по экспоненциальному закону, в Excel предусмотрена стандартная функция ЛОГНОРМРАСП(…) – рис. П1.22, П1.23, которая вызывается из пункта меню Вставка ¾ Функция ¾ Кате-

гория «Статистические» ¾ ЛОГНОРМРАСП (… ).

Рис. П1.22.

218

Рис. П1.23.

y Вероятность того, что значения случайной величины X примут значения, меньшие, чем a:

P( x < a) = ЛОГНОРМРАСП ( a; μx ; σx ) .

y Вероятность того, что значения случайной величины X примут значения, большие, чем b:

P( x > b) = 1 – ЛОГНОРМРАСП ( b; μx ; σx )

y Вероятность того, что значения случайной величины X будут находиться в диапазоне от a до b:

P(a < x < b) = ЛОГНОРМРАСП ( b; μx ; σx ) –

– ЛОГНОРМРАСП ( a; μx ; σx ) .

219

ОСНОВНЫЕ ТЕРМИНЫ (ГЛОССАРИЙ)

Случайная величина – величина, относительно которой заранее нельзя сказать, какое в точности значение она примет.

Дискретная случайная величина – случайная величина, все возможные значения которой можно перечислить или пронумеровать и

Непрерывная случайная величина – случайная величина,

все возможные значения которой непрерывно заполняют некоторый промежуток.

Закон (ряд) распределения дискретной, случайной вели-

чины – соотношение, связывающее между собой ее возможные значения с соответствующими им вероятностями.

Функция распределения (интегральная функция распределения) непрерывной случайной величины – функция вида

F(xi) = P (X < xi) – вероятность того, что случайная величина примет значения, не большее, чем xi .

Функция плотности вероятности – функция, связанная с интегральной функцией распределения F(x) соотношением f (x) = F′(x) . Используется, наряду с F(x) для задания закона распределения непрерывной случайной величины.

Числовые характеристики случайной величины – харак-

теристики, которые в сжатой форме отражают наиболее существенные особенности случайной величины и ее закона распределения. К ним относятся математическое ожидание, дисперсия, стандартное отклонения случайной величины и некоторые другие.

Математическое ожидание случайной величины – среднее

(ожидаемое) значение случайной величины. Обозначается символами μ или М(Х), в зарубежной литературе – E(Х) (от англ. Expected – ожидаемый).

Дисперсия – «мера» степени разброса значений случайной величины относительного среднего (математического ожидания). Обозначается символом D или σ 2 = D .

Стандартное отклонение – «мера» степени разброса значений случайной величины относительного среднего (математиче-

ского ожидания). Корень квадратный из дисперсии σ = D .

220

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 3122 23 24 25 26 27 28 29 30 31 > Следующая >>>