§11. Свойства двумерной плотности вероятности

Свойство 1. Двумерная плотность вероятности неотрицательна:

f(x, у)≥0.

Доказательство. Вероятность попадания случайной точки в прямоугольник со сторонами x и есть неотрицательное число; площадь этого прямоугольника - положительное число. Следовательно, отношение этих двух чисел, а значит, и их предел (прии), который равен f(x, у) (см. § 9), есть неотрицательное число, т. е.

f(x, у)≥0.

Заметим, что свойство непосредственно следует из того, что F (x,у) - неубывающая функция своих аргументов (§ 4).

Свойство 2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:

.

Доказательство. Бесконечные пределы интегрирования указывают, что областью интегрирования служит вся плоскость xОy; поскольку событие, состоящее в том, что случайная точка попадет при испытании на плоскость xОy, достоверно, то вероятность этого события (она и определяется двойным несобственным интегралом от двумерной плотности) равна единице, т. е.

.

Пример. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, У): f(x, у)С cos x cos у в квадрате, ; вне этого квадратаf(x, у)=0.

Найти постоянный параметр С.

Решение. Воспользуемся свойством 2, учитывая, что x и y изменяются от 0 до /2:

С.

Отсюда

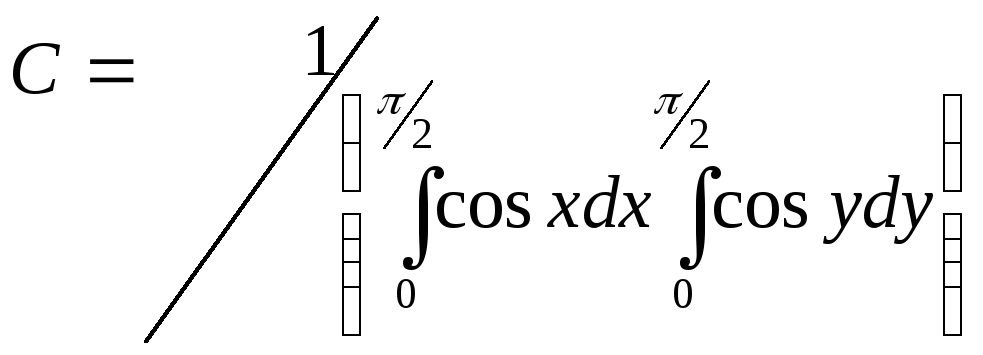
Выполнив интегрирование, получим искомое значение параметра С=1.

§ 12. Отыскание плотностей вероятности составляющих двумерной случайной величины

Пусть известна плотность совместного распределения вероятностей системы двух случайных величин. Найдем плотности распределения каждой из составляющих.

Найдем сначала плотность распределения составляющей X. Обозначим через F₁(x) функцию распределения, составляющей X. По определению плотности распределения одномерной случайной величины,

.

Приняв во внимание соотношения

(см.§8),

(см.§4),

найдем

Продифференцировав обе части этого равенства по x, получим

,

или

. (*)

Аналогично находим плотность распределения составляющей Y:

. (**)

Итак, плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей.

Пример. Двумерная случайная величина (X, У) задана плотностью совместного распределения

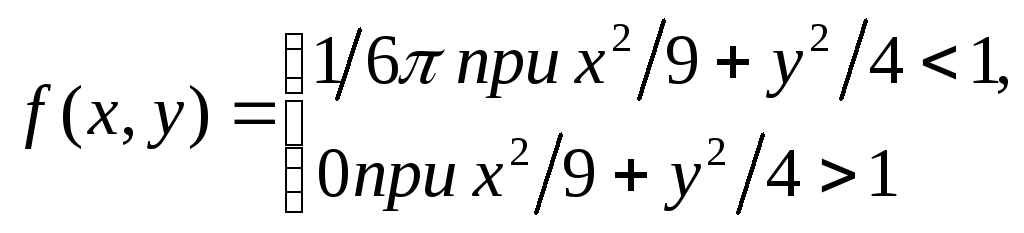
Найти плотности распределения составляющих X и Y.

Решение. Найдем плотность распределения составляющей X по формуле (*):

.

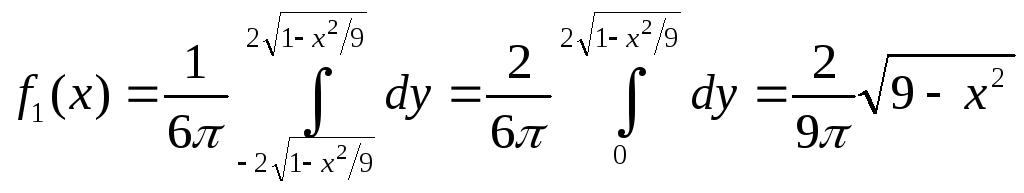Итак,

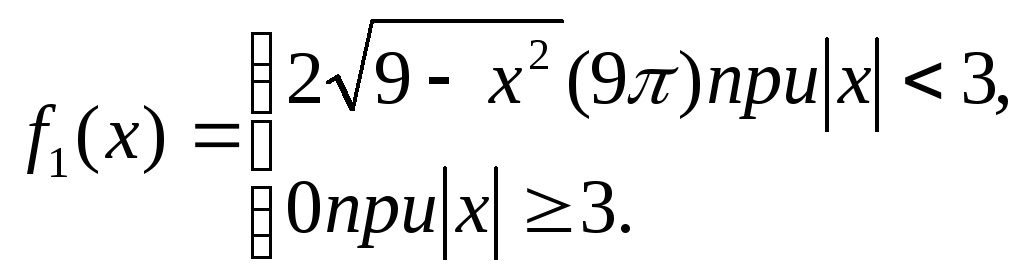
Аналогично, используя формулу (**), найдем плотность распределения составляющей Y:

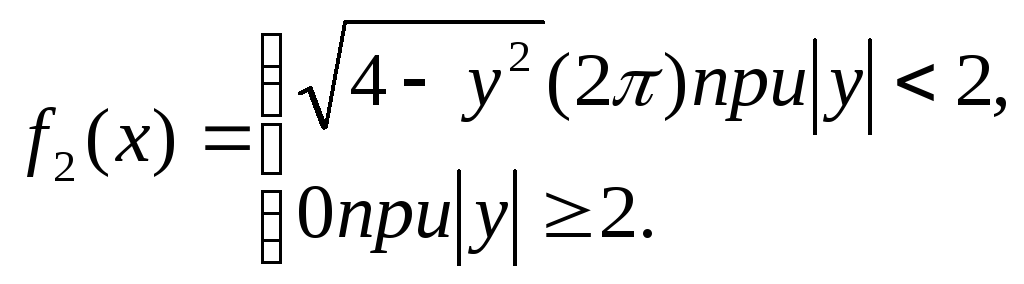
Рекомендуем читателю для контроля самостоятельно убедиться в том, что найденные функции удовлетворяют соотношениям

и.

§ 13. Условные законы распределения составляющих системы дискретных случайных величин

Известно, что если события А и В зависимы, то условная вероятность события В отличается от его безусловной вероятности. В этом случае (см. гл. III, § 2)

. (*)

Аналогичное положение имеет место и для случайных величин. Для того чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, введем понятие условного распределения.

Рассмотрим дискретную двумерную случайную величину (X,Y). Пусть возможные значения составляющих таковы: х₁ х₂, .... х_п; у₁, у₂ ..., у_т.

Допустим, что в результате испытания величина Y приняла значение Y= у₁; при этом X примет одно из своих возможных значений: х₁, или х₂, ..., или х_n. Обозначим условную вероятность того, что X примет, например, значение х₁ при условии, что Y=у₁, через р(х₁|у₁). Эта вероятность, вообще говоря, не будет равна безусловной вероятности р(х₁).

В общем случае условные вероятности составляющей будем обозначать так:

p(x_i|y_j) (i=1, 2, …, n; j=1, 2, …, m).

Условным распределением составляющей X при Y=у₁ называют совокупность условных вероятностей p(x₁|y_j), p(x₂|y_j), …, p(x_n|y_j) вычисленных в предположении, что событие Y=у_j (j имеет одно и то же значение при всех значениях X) уже наступило. Аналогично определяется условное распределение составляющей Y.

Зная закон распределения двумерной дискретной случайной величины, можно, пользуясь формулой (*), вычислить условные законы распределения составляющих. Например, условный закон распределения X в предположении, что событие Y=у₁ уже произошло, может быть найден по формуле

(i=1, 2, …, n).

В общем случае условные законы распределения составляющей X определяются соотношением

(**)

Аналогично находят условные законы распределения составляющей Y:

. (***)

Замечание. Сумма вероятностей условного распределения равна единице.

Действительно, так как при фиксированном y_i имеем (см. § 2)

, то

.

Аналогично доказывается, что при фиксированном x_i

.

Это свойство условных распределений используют для контроля вычислений.

Пример. Дискретная двумерная случайная величина задана табл. 4.

Таблица 4

Y	X
	x1	x2	x3
y1 y2	0,10 0,06	0,30 0,18	0,20 0,16

Найти условный закон распределения составляющей X при условии, что составляющая Y приняла значение y₁.

Решение. Искомый закон определяется совокупностью следующих условных вероятностей:

p(x₁|y₁), p(x₂|y1), p(x₃|y₁).

Воспользовавшись формулой (*) и приняв во внимание, что p (y₁) = 0,60 (см. § 2, пример), имеем:

p(x₁|y₁)= p(x₁,y₁)/p(y₁)=0,10/0,60=1/6,

p(x₂|y₁) =p(x₂,y₁)/p(y₁)=0,30/0,60=1/2,

p(x₃|y₁)= p(x₃,y₁)/p(y₁)=0,20/0,60=1/3.

Сложив для контроля найденные условные вероятности, убедимся, что их сумма равна единице, как и должно быть, в соответствии с замечанием, помещенным выше: 1/6+1/2+ 1/3=1.