§ 8. Нахождение функции распределения системы по известной плотности распределения

Зная плотность совместного распределения f(x,у), можно найти функцию распределения F(x,у) по формуле:

что непосредственно следует из определения плотности распределения двумерной непрерывной случайной величины (X, У).

Пример. Найти функцию распределения двумерной случайной величины по данной плотности совместного распределения

Решение. Воспользуемся формулой:

.

Положив

, получим

=

=.

§ 9. Вероятностный смысл двумерной плотности вероятности.

Вероятность попадания случайной точки (X;Y) в прямоугольник АВСD (рис. 16) равна (см. § 6)

Р (х₁ < X < х₂, у₁ < Y < у₂)= [F(x₂, у₂) - F(x₁, у₂)] - [F(x₂, у₁) - F(x₁, у₁)].

Обозначив для краткости левую часть равенства через P_abcd и применив к правой части теорему Лагранжа, получим

P_abcd=,

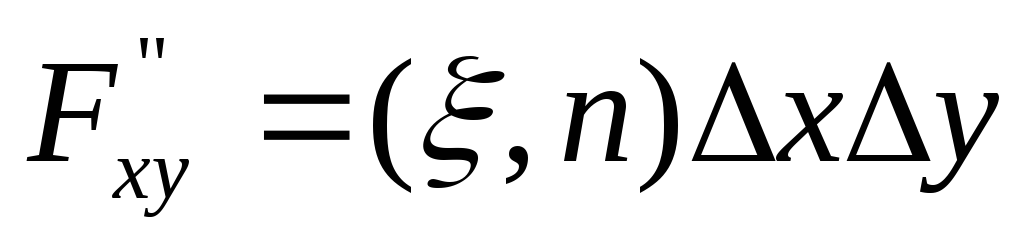где

.

Отсюда

=,

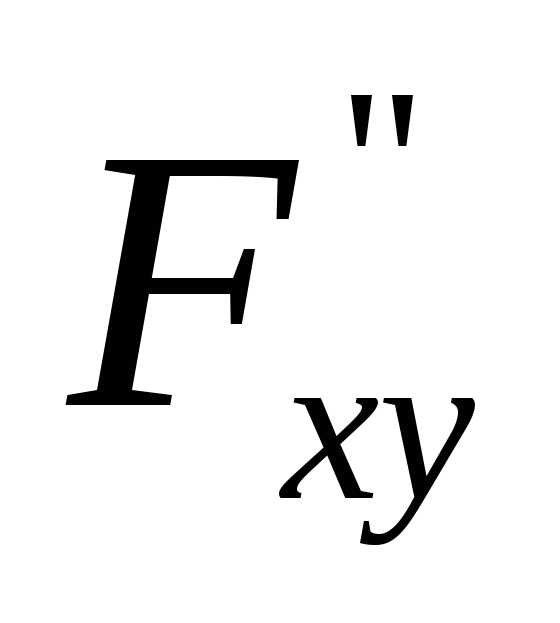
или

f=. (**)

Приняв во внимание, что произведение равно площади прямоугольникаABCD, заключаем:fесть отношение вероятности попадания случайной точки в прямоугольникABCDк площади этого прямоугольника.

П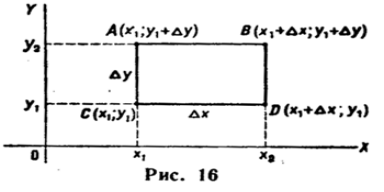ерейдем теперь в равенство (**) к пределу при. Тогдаи, следовательно,

.

Итак, функцию можно рассматривать как предел отношения вероятности попадания случайной точки в прямоугольник (со сторонамии) к площади этого прямоугольника, когда обе стороны прямоугольник стремятся к нулю.

§ 10. Вероятность попадания случайной точки в произвольную область

Перепишем соотношение (**) §9 так: f=.

О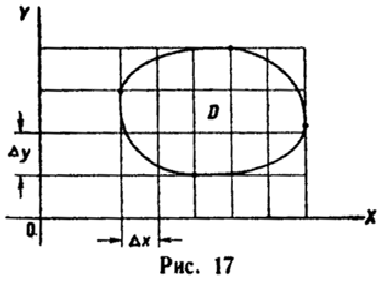тсюда заключаем: произведение

fесть вероятность попадания случайной точки в прямоугольник со сторонами .

Пусть в плоскости xОy задана произвольная область D. Обозначим событие, состоящее в попадании случайной точки в эту область, так: (X, У).

Разобьем область D на п элементарных областей прямыми, параллельными оси Оy, находящимися на расстоянии x одна от другой, и прямыми, параллельными оси Ох, находящимися на расстоянии одна от другой (рис. 17) (для простоты предполагается, что эти прямые пересекают контур области не более чем в двух точках). Так как события, состоящие в попадании случайной точки в элементарные области, несовместны, то вероятность попадания в областьD приближенно (сумма элементарных областей приближенно равна области D) равна сумме вероятностей попаданий точки в элементарные области:

.

Переходя к пределу при и, получим

=. (*)

Итак, для того чтобы вычислить попадание случайной точки (X,Y) в областьD, достаточнонайти двойной интеграл по области D от функции f(x,y).

Геометрически равенство (*) можно истолковать так: вероятность попадания случайной точки (X,Y)в область D равна объему тела, ограниченного сверху поверхностью z = f(x,у), основанием которого служит проекция этой поверхности на плоскость xOy.

Замечание. Подынтегральное выражение f (x,у)dxdу называют элементом вероятности. Как следует из предыдущего, элемент вероятности определяет вероятность попадания случайной точки в элементарный прямоугольник со сторонами dx и dу.

Пример. Плотность распределения двумерной случайной величины

.

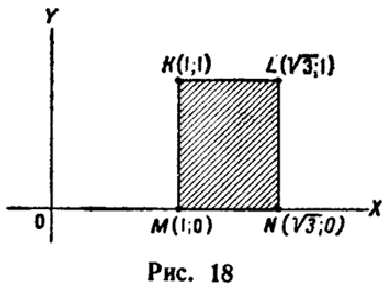
Найти вероятность попадания случайной точки в прямоугольник (рис. 18) с вершинами K(1,1), L(,1), M(1,0), N(,0).

Решение. Искомая вероятность

==

=

=.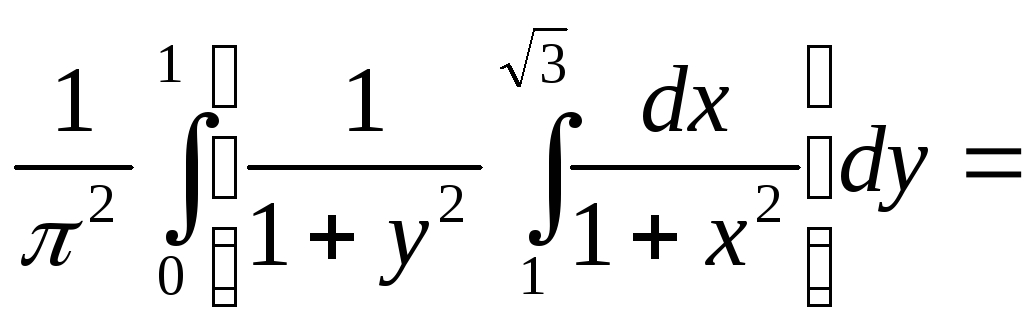