§ 17. Оценка истинного значения измеряемой величины

Пусть производится п независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины X_l, Х₂ ,… , Х_n. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии σ² (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в двух предыдущих параграфах, выполняются, и, следовательно, мы вправе использовать полученные в них формулы. Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов. Поскольку обычно σ неизвестно, следует пользоваться формулами, приведенными в § 16.

Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметической результатов отдельных измерений =42,319 и «исправленное» среднее квадратическое отклонение s=5,0. Требуется оценить истинное значение измеряемой величины с надежностью γ=0,95.

Решение. Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном σ) при помощи доверительного интервала

,

покрывающего а с заданной надежностью γ = 0,95.

Пользуясь таблицей приложения 3, по γ = 0,95 и n= 9 находим t_γ = 2,31.

Найдем точность оценки:

.

Найдем доверительные границы:

= 42,319 - 3,85 = 38,469;

= 42,319+3,85 = 46,169.

Итак, с надежностью 0,95 истинное значение измеряемой величины заключено в доверительном интервале

38,469 < а < 46,169.

§ 18. Доверительные интервалы для оценки среднего квадратического отклонения σ нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение σ по «исправленному» выборочному среднему квадратическому отклонению s. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр σ с заданной надежностью γ.

Потребуем, чтобы выполнялось соотношение

Р(|σ-s|<δ)= γ, или P(s-δ<σ<s+δ) = γ.

Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство

s-δ<σ<s+δ

в равносильное неравенство

s(1-δ/s)<σ<s(1+δ/s).

Положив δ/s = q, получим

s(1-q)<σ<s(1+q). (*)

Остается найти q. С этой целью введем в рассмотрение случайную величину «хи»:

где п - объем выборки.

Как было указано [см. § 16, пояснение, соотношение (***)], величина S²(n—1)/σ² распределена по закону χ² с п-1 степенями свободы, поэтому квадратный корень из нее обозначают через χ.

Плотность распределения χ имеет вид (см. пояснение в конце параграфа)

. (**)

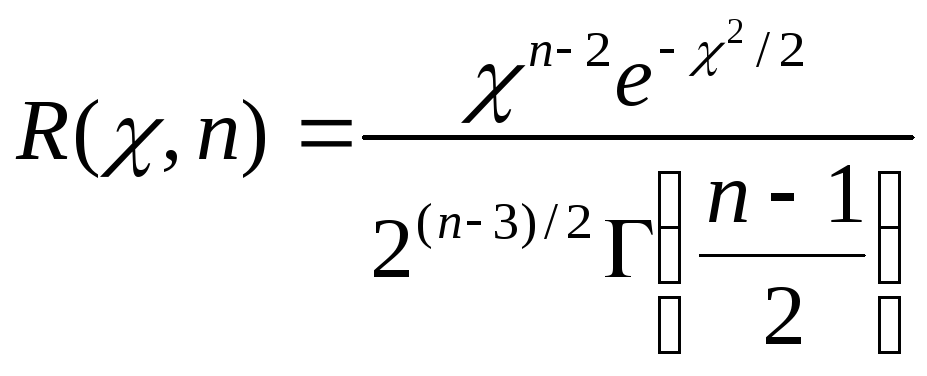Это распределение не зависит от оцениваемого параметра σ, а зависит лишь от объема выборки п.

Преобразуем неравенство (*) так, чтобы оно приняло вид χ₁< χ< χ₂. Вероятность этого неравенства (см. гл. XI, § 2) равна заданной вероятности γ, т.е.

.

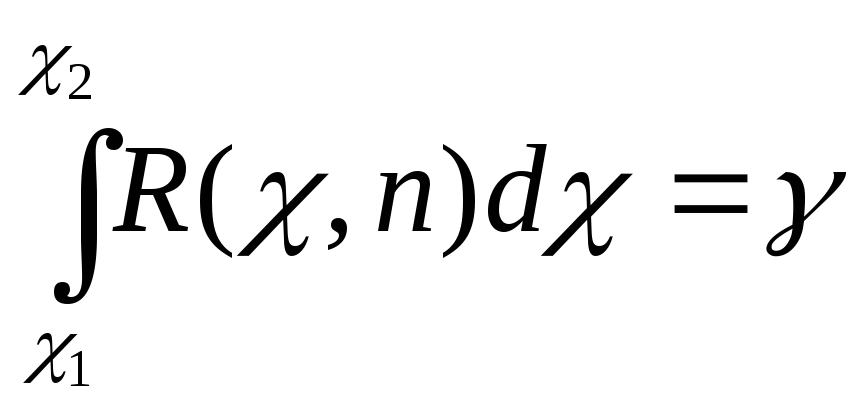Предполагая, что q < 1, перепишем неравенство (*) так:

.

Умножив все члены неравенства на , получим

, или.

Вероятность того, что это неравенство, а следовательно, и равносильное ему неравенство (*) будет осуществлено, равна

.

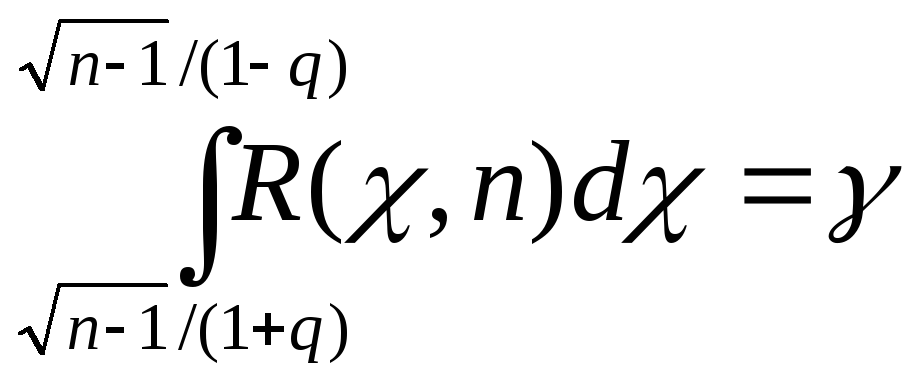Из этого уравнения можно по заданным п и γ найти q. Практически для отыскания q пользуются таблицей приложения 4.

Вычислив по выборке s и найдя по таблице q, получим искомый доверительный интервал (*), покрывающий σ с заданной надежностью γ, т. е. интервал

s(1-q)<σ<s(1+q).

Пример 1. Количественный признак X генеральной совокупности распределен нормально. По выборке объема п = 25 найдено «исправленное» среднее квадратическое отклонение s = 0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,95.

Решение. По таблице приложения 4 по данным γ = 0,95 и n = 25 найдем q = 0,32.

Искомый доверительный интервал (*) таков:

0,8 (1—0,32) < σ < 0,8 (1+0,32), или 0,544 < σ < 1,056.

Замечание. Выше предполагалось, что q < 1. Если q > 1, то неравенство (*) примет вид (учитывая, что σ > 0)

0 < σ< s (1+q),

или (после преобразований, аналогичных случаю q < 1)

Следовательно, значения q > 1 могут быть найдены из уравнения

Практически для отыскания значений q > 1, соответствующих различным заданным n и γ, пользуются таблицей приложения 4.

Пример 2. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=10 найдено «исправленное» среднее квадратическое отклонение s=0,16. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,999.

Решение. По таблице приложения 4 по данным γ=0,999 и n =10 найдем q=1,80 (q>1). Искомый доверительный интервал таков:

0 < σ < 0,16(1 + 1,80), или 0 < σ < 0,448.

Пояснение. Покажем, что плотность распределения χ имеет вид (**).

Если случайная величина X распределена по закону χ² с k = n-1 степенями свободы, то ее плотность распределения (см. гл. XII, § 13)

,

или после подстановки k= n-1

.

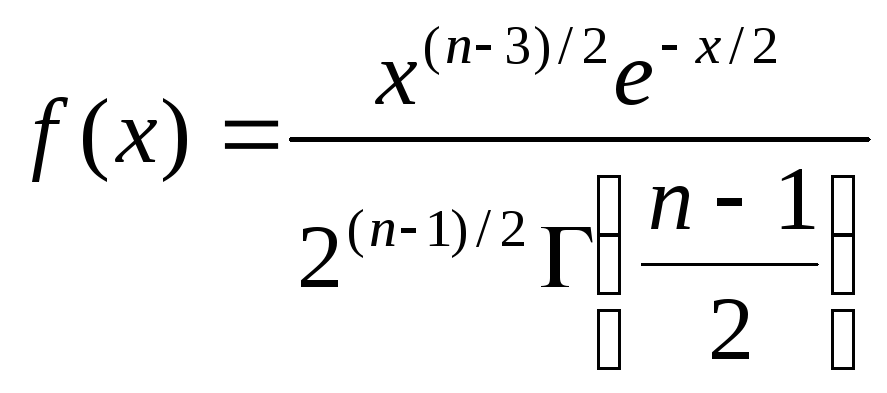Воспользуемся формулой (см. гл. XII, § 10)

,

чтобы найти распределение функции .Отсюда обратная функция

и.

Так как χ > 0, то , следовательно,

.

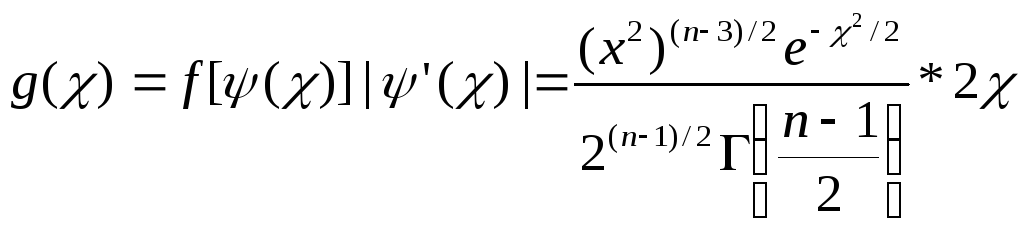Выполнив элементарные преобразования и изменив обозначения (g(χ), заменим на R(χ, n)), окончательно получим

.
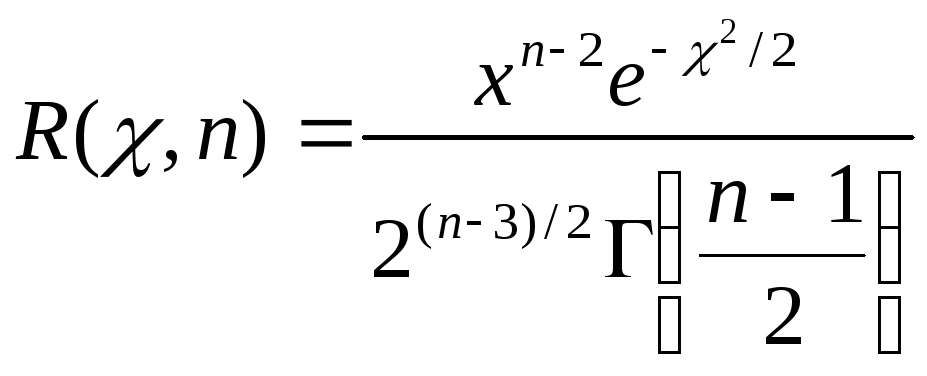