§ 16. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение а неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором σ предполагалось известным.

Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t):

,

которая имеет распределение Стьюдента с k = n-1 степенями свободы (см. пояснение в конце параграфа); здесь - выборочная средняя, S - «исправленное» среднее квадратическое отклонение, n - объем выборки.

Плотность распределения Стьюдента

,

где .

Мы видим, что распределение Стьюдента определяется параметром n - объемом выборки (или, что то же, числом степеней свободы k = n-1) и не зависит от неизвестных параметров а и σ; эта особенность является его большим достоинством. Поскольку S(t,n) - четная функция от t, вероятность осуществления неравенства определяется так (см. гл. § XI, 2, замечание):

.

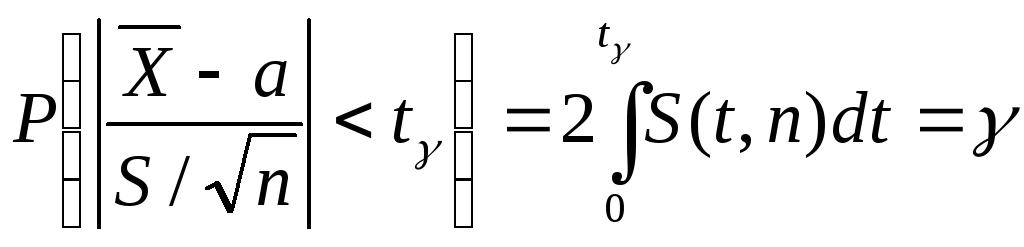Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим

.

Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал , покрывающий неизвестный параметр а с надежностью γ.

Здесь случайные величины и S заменены неслучайными величинами и s, найденными по выборке. По таблице приложения 3 по заданным n и γ можно найти t_γ .

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n =16 найдены выборочная средняя = 20,2 и «исправленное» среднее квадратическое отклонениеs = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение. Найдем t_γ. Пользуясь таблицей приложения 3, по γ = 0,95 и n = 16 находим t_γ =2,13.

Найдем доверительные границы:

.

.

Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале

19,774 < а < 20,626.

Замечание. Из предельных соотношений

.

следует, что при неограниченном возрастании объема выборки n распределение Стьюдента стремится к нормальному. Поэтому практически при n > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением.

Однако важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений n, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т.е. к повышению точности оценки. Например, если n = 5 и γ = 0,99, то, пользуясь распределением Стьюдента, найдем t_γ = 4,6 , а используя функцию Лапласа, найдем t_γ = 2,58, т.е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.

То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке.

Пояснение. Ранее было указано (см. гл. XII, § 14), что если Z - нормальная величина, причем M(Z) = 0, σ(Z)=1, а V- независимая от Z величина, распределенная по закону χ² с k степенями свободы, то величина

(*)

распределена по закону Стьюдента с k степенями свободы. Пусть количественный признак X генеральной совокупности распределен нормально, причем М(Х)=а, σ(Х)= σ. Если из этой совокупности извлекать выборки объема n и по ним находить выборочные средние, то можно доказать, что выборочная средняя распределена нормально, причем (см. гл. VIII, § 9)

, .

Тогда случайная величина

(**)

также имеет нормальное распределение как линейная функция нормального аргумента (см. гл.XII, § 10, замечание), причем М (Z) = 0, σ(Z)=l. Доказано, что случайные величины Z и

(***)

независимы (S² - исправленная выборочная дисперсия) и что величина V распределена по закону χ² с k = n-1 степенями свободы.

Следовательно, подставив (**) и (***) в (*), получим величину

,

которая распределена по закону Стьюдента с k = n-1 степенями свободы.