§ 12. Сложение дисперсий

Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:

D_общ =D_внгр + D_межгр.

Доказательство. Для упрощения доказательства предположим, что вся совокупность значений количественного признака X разбита на две следующие группы:

Группа……………………	первая		вторая
Значение признака………..	x1 x2		x1 x2
Частота…………………….	m1 m2		n1 n2
Объем группы…………….	N1= m1+ m2		N2= n1+ n2
Групповая средняя……….
Групповая дисперсия…….
Объем своей совокупности	n=N1+N2

Далее для удобства записи вместо знака суммы пишется знак.

Например, .

Следует также иметь в виду, что если под знаком суммы стоит постоянная величина, то ее целесообразно выносить за знак суммы.

Например, .

Найдем общую дисперсию:

D_общ=. (*)

Преобразуем первое слагаемое числителя, вычтя и прибавив :

.

Так как

(равенство следует из соотношения ) и в силу § 7

,

тo первое слагаемое принимает вид

. (**)

Аналогично можно представить второе слагаемое числителя (*) (вычтя и прибавив):

. (***)

Подставим (**) и (***) в (*):

.

Итак,

D_общ =D_внгр + D_межгр.

Пример, иллюстрирующий доказанную теорему, приведен в предыдущем параграфе.

Замечание. Теорема имеет не только теоретическое, но и важное практическое значение. Например, если в результате наблюдений получены несколько групп значений признака, то для вычисления общей дисперсии можно группы в единую совокупность не объединять. С другой стороны, если совокупность имеет большой объем, то целесообразно разбить ее на несколько групп. В том и другом случаях непосредственное вычисление общей дисперсии заменяется вычислением дисперсий отдельных групп, что облегчает расчеты.

§ 13. Оценка генеральной дисперсий по исправленной выборочной

Пусть из генеральной совокупности в результате n независимых наблюдений над количественным признаком X извлечена повторная выборка объема n:

значения признака………	x1	x2	…	xk
частоты…………………...	n1	n2	…	nk

При этом n₁ + n₂ + ... + n_k = п.

Требуется по данным выборки оценить (приближенно найти) неизвестную генеральную дисперсию D_г. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная дисперсия является смещенной оценкой D_г, другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

.

Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить D_в на дробь n/(n-1). Сделав это, получим исправленную дисперсию, которую обычно обозначают через s²:

.

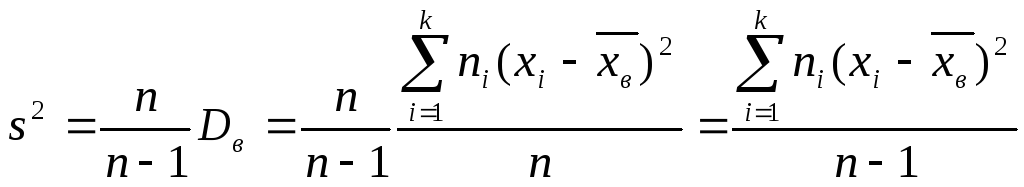Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии. Действительно,

.

Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию

.

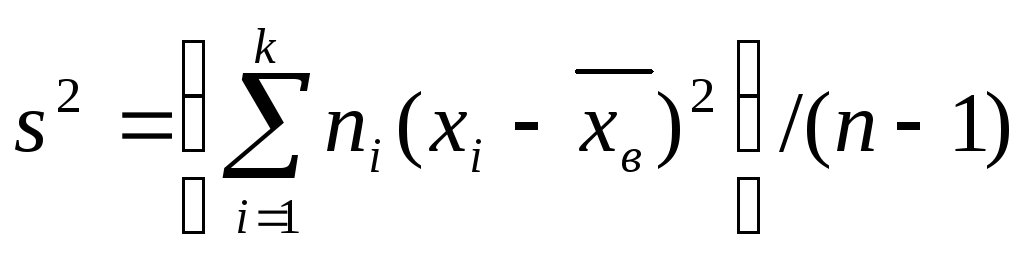Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:

.

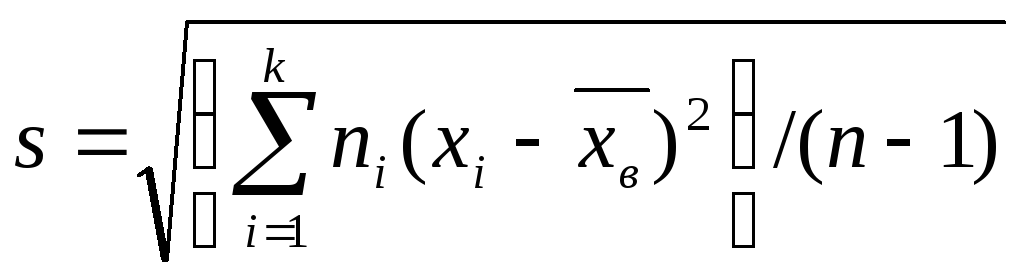Подчеркнем, что s не является несмещенной оценкой; чтобы отразить этот факт, мы написали и будем писать далее так: «исправленное» среднее квадратическое отклонение.

Замечание. Сравнивая формулы

и .

видим, что они отличаются лишь знаменателями. Очевидно, при достаточно больших значениях n объема выборки выборочная и исправленная дисперсии различаются мало. На практике пользуются исправленной дисперсией, если примерно n < 30.